当前位置:网站首页>[mathematical logic] equivalent calculus and reasoning calculus of predicate logic (individual word | predicate | quantifier | predicate logic formula | two basic formulas | proposition symbolization
[mathematical logic] equivalent calculus and reasoning calculus of predicate logic (individual word | predicate | quantifier | predicate logic formula | two basic formulas | proposition symbolization
2022-07-03 17:28:00 【Programmer community】
List of articles
- One 、 Predicate logic related concepts
- 1、 Individual words
- 2、 The predicate
- 3、 quantifiers
- Two 、 First order predicate logic formula
- 3、 ... and 、 Two basic formulas
- 1、 Formula 1
- 2、 Formula 2
- Four 、 Propositional symbolization skills
- 1、 Propositional Symbolization Method
- 2、 Predicate logical combination
- 3、 If and only if predicate logic
- 5、 ... and 、 Examples of propositional symbolization
Reference blog :
- 【 Mathematical logic 】 Predicate logic ( Individual words | Individual domain | The predicate | Full name quantifier | There are quantifiers | Predicate formula | exercises )
- 【 Mathematical logic 】 Predicate logic ( First order predicate logic formula | Example )
- 【 Mathematical logic 】 Predicate logic ( Judge whether the first-order predicate logic formula is true or false | explain | Example | Predicate logic formula type | Yongzhen style | Permanent falsehood | Satisfiability | Equivalent formula )
- 【 Mathematical logic 】 Predicate logic ( Basic equivalence of predicate logic | Eliminate quantifier equivalents | The quantifier negates the equivalent | The scope of quantifier is shrinking and expanding | The equivalent of quantifier distribution )
- 【 Mathematical logic 】 Predicate logic ( The toe in paradigm | The method of toe in normal form transformation | Basic equivalence of predicate logic | Name change rules | Predicate logic inference law )
One 、 Predicate logic related concepts
1、 Individual words
Individual words :
① individual source : First order predicate logic in , take Atomic proposition Divide into The subject and Predicate , Here we have Individual words And The predicate Of Concept ;
② individual Concept : take Independent object , Concrete things , Abstract things ( Concept ) be called individual or Individual words ;
③ individual Argument : Use
a
,
b
,
c
a,b,c
a,b,c Represents an individual argument ;
④ individual Changyuan : Use
x
,
y
,
z
x, y, z
x,y,z Represents individual constant ;
⑤ Individual domain Concept : individual Argument The value of be called Individual domain ;
⑥ Individual domain Value : Individual domain Sure Value Finite set or Infinite set ;
⑦ Total individual domain : Everything in the universe Composed of Individual domain be called Total individual domain ;
A proposition is a statement , The declarative sentence is composed of The subject , Predicate , The object form , The subject object is the individual , Predicate is predicate ;
Predicate logic from individual , The predicate , quantifiers form ;
2、 The predicate
The predicate :
① Predicate concept : Will represent Individual nature or Relationship between each other Of word be called The predicate ;
② The predicate indicates : Use
F
,
G
,
H
F, G, H
F,G,H Representation predicate Changyuan or Argument ;
③ The individual property predicate indicates :
F
(
x
)
F(x)
F(x) Express
x
x
x have nature
F
F
F , Such as
F
(
x
)
F(x)
F(x) Express
x
x
x It's black ;
④ Examples of relational property predicates :
F
(
x
,
y
)
F(x, y)
F(x,y) Express
x
,
y
x, y
x,y have Relationship F , Such as :
F
F
F
G
(
x
,
y
)
G(x, y)
G(x,y) Express
x
x
x Greater than
y
y
y ;
There are quantifiers :Exist Medium E Turn left and right, then turn upside down ;
① Language correspondence : Corresponding Natural language in “ There is one ” , “ There is a ” , “ yes , we have ” etc. ;
② Representation : Using symbols
∃
\exist
∃ Express ;
③ Reading 1 :
∃
x
\exist x
∃x Represents the individual domain There are
x
x
x ;
④ Reading 2 :
∃
x
(
F
(
x
)
)
\exist x( F(x) )
∃x(F(x)) Express , In the individual domain There is
x
x
x Have the quality of
F
F
F ;
3、 quantifiers
Full name quantifier :Any Medium A Upside down ;
① Language correspondence : Corresponding Natural language in “ arbitrarily ” , “ be-all ” , “ every last ” etc. ;
② Representation : Using symbols
∀
\forall
∀ Express ;
③ Reading 1 :
∀
x
\forall x
∀x Represents the individual domain be-all
x
x
x ;
④ Reading 2 :
∀
x
(
F
(
x
)
)
\forall x( F(x) )
∀x(F(x)) Express , All in the individual domain
x
x
x All have properties
F
F
F ;
Reference blog : 【 Mathematical logic 】 Predicate logic ( Individual words | Individual domain | The predicate | Full name quantifier | There are quantifiers | Predicate formula | exercises )
Two 、 First order predicate logic formula
Propositional formula : Basic proposition ( Propositional constant / Argument ) and A number of Conjunctions Form a finite length string ;
① Single Propositional argument / Propositional constant Is a proposition formula ;
② If
A
A
A Is a proposition formula , be
(
¬
A
)
(\lnot A)
(¬A) It is also a propositional formula ;
③ If
A
,
B
A,B
A,B Is a proposition formula , be
(
A
∧
B
)
,
(
A
∨
B
)
,
(
A
→
B
)
,
(
A
B
)
(A \land B) , (A \lor B), (A \to B), (A \leftrightarrow B)
(A∧B),(A∨B),(A→B),(AB) It is also a propositional formula ;
④ A limited number of times application ① ② ③ Formed symbol string Is a proposition formula ; ( Infinite times cannot )
First order predicate logic formula : stay Propositional formula On the basis of , Add a condition :
If
A
A
A It's the formula , be
∀
x
A
\forall x A
∀xA and
∃
x
A
\exist x A
∃xA Is also a formula
Related concepts of first-order predicate logic formula : With
∀
x
A
\forall x A
∀xA ,
∃
x
A
\exist x A
∃xA Take the formula as an example ;
Guide arguments :
∀
,
∃
\forall , \exist
∀,∃ After quantifier
x
x
x be called Guide arguments
Jurisdiction :
A
A
A be called The scope of the corresponding quantifier ;
Constraints appear : stay
∀
x
\forall x
∀x ,
∃
x
\exist x
∃x Jurisdiction
A
A
A in ,
x
x
x All appearances are constrained , This is called constraint occurrence ;
Free to appear : Jurisdiction
A
A
A in , It is not the argument of the constraint , Are free to appear ;
Reference blog : 【 Mathematical logic 】 Predicate logic ( First order predicate logic formula | Example )
3、 ... and 、 Two basic formulas
1、 Formula 1
In the individual domain all There is a quality
F
F
F Of individual , all have nature
G
G
G ;
Use predicate logic to express :
①
F
(
x
)
F(x)
F(x) :
x
x
x Have the quality of
F
F
F ;
②
G
(
x
)
G(x)
G(x) :
x
x
x Have the quality of
G
G
G ;
③ The proposition is symbolized as :
∀
x
(
F
(
x
)
→
G
(
x
)
)
\forall x ( F(x) \rightarrow G(x) )
∀x(F(x)→G(x))
2、 Formula 2
Individual domain in Existence has nature
F
F
F At the same time, it has the nature of
G
G
G The individual of ;
Use predicate logic to express :
①
F
(
x
)
F(x)
F(x) :
x
x
x Have the quality of
F
F
F ;
②
G
(
x
)
G(x)
G(x) :
x
x
x Have the quality of
G
G
G ;
③ The proposition is symbolized as :
∃
x
(
F
(
x
)
∧
G
(
x
)
)
\exist x ( F(x) \land G(x) )
∃x(F(x)∧G(x))
Four 、 Propositional symbolization skills
1、 Propositional Symbolization Method
Propositional Symbolization Method :
① Write individual fields : The first Individual domain Write clearly , namely indicate
∀
x
\forall x
∀x , representative Everything , If it's everything , Then it must be indicated that it is the total individual domain ;
② Write a relational predicate : Use
F
,
G
,
H
F , G , H
F,G,H indicate Individual nature or Relationship ;
③ Propositional symbols : take Proposition symbolization result Indicate the , It's best to bring a detailed explanation ;
2、 Predicate logical combination
from Full name quantifier or There are quantifiers Individual words The predicate Combined Predicate logic , You can also think of it as One Predicate logic
F
(
x
)
F(x)
F(x) or
G
(
x
,
y
)
G(x, y)
G(x,y) parts Combine again ;
as follows Predicate logic :
∀
x
(
F
(
x
)
→
∀
y
(
G
(
y
)
→
H
(
x
,
y
)
)
)
\forall x (F(x) \rightarrow \forall y ( G(y) \rightarrow H(x,y) ))
∀x(F(x)→∀y(G(y)→H(x,y)))
among
∀
y
(
G
(
y
)
→
H
(
x
,
y
)
)
\forall y ( G(y) \rightarrow H(x,y) )
∀y(G(y)→H(x,y)) It's already assembled Predicate logic , Now think of it as a nature , perhaps Predicate logic unit
A
A
A , Combine again more complex and Gigantic Predicate logic , Get the following :
∀
x
(
F
(
x
)
→
A
)
\forall x (F(x) \rightarrow A)
∀x(F(x)→A)
therefore , Above Predicate logic After deployment , You get the first
∀
x
(
F
(
x
)
→
∀
y
(
G
(
y
)
→
H
(
x
,
y
)
)
)
\forall x (F(x) \rightarrow \forall y ( G(y) \rightarrow H(x,y) ))
∀x(F(x)→∀y(G(y)→H(x,y)))
3、 If and only if predicate logic
If and only if Predicate logic Symbolization :
( 1 ) The third variable : Make sure to introduce The third party The variable of ;
( 2 ) nature or Relationship positive Deduce : The general pattern is
① For all
x
x
x And There is a
y
y
y Yes A certain quality or relationship ,
② For all
x
x
x and be-all
z
z
z There is a certain nature or relationship ;
③
y
y
y And
z
z
z Having equal attributes ;
( 3 ) nature or Relationship Back to back : The general pattern is
① For all
x
x
x And There is a
y
y
y Yes A certain quality or relationship ,
②
y
y
y And be-all
z
z
z There is another property or Relationship , Generally equal or Unequal Relationship ,
③ Can be launched
x
x
x and
z
z
z Yes perhaps No, some nature or Relationship ;
5、 ... and 、 Examples of propositional symbolization
Reference resources : 【 Mathematical logic 】 Predicate logic ( Individual words | Individual domain | The predicate | Full name quantifier | There are quantifiers | Predicate formula | exercises ) 3、 ... and . Proposition symbolization exercises
边栏推荐
- Depth first search of graph
- How SVN views modified file records
- SVN完全备份svnadmin hotcopy
- 数仓任务里面 跑SQL任务的时候用的数据库账号是在哪里配置的
- Redis: operation commands for list type data
- LeetCode13.罗马数字转整数(三种解法)
- SQL injection database operation foundation
- SVN如何查看修改的文件记录
- Vs2013 has blocked the installer, and ie10 needs to be installed
- 大消费企业怎样做数字化转型?
猜你喜欢

Wechat applet for the first time
How to train mask r-cnn model with your own data
![[RT thread] NXP rt10xx device driver framework -- Audio construction and use](/img/85/32a83eaa4b7f5b30d4d7c4f4c32791.png)
[RT thread] NXP rt10xx device driver framework -- Audio construction and use
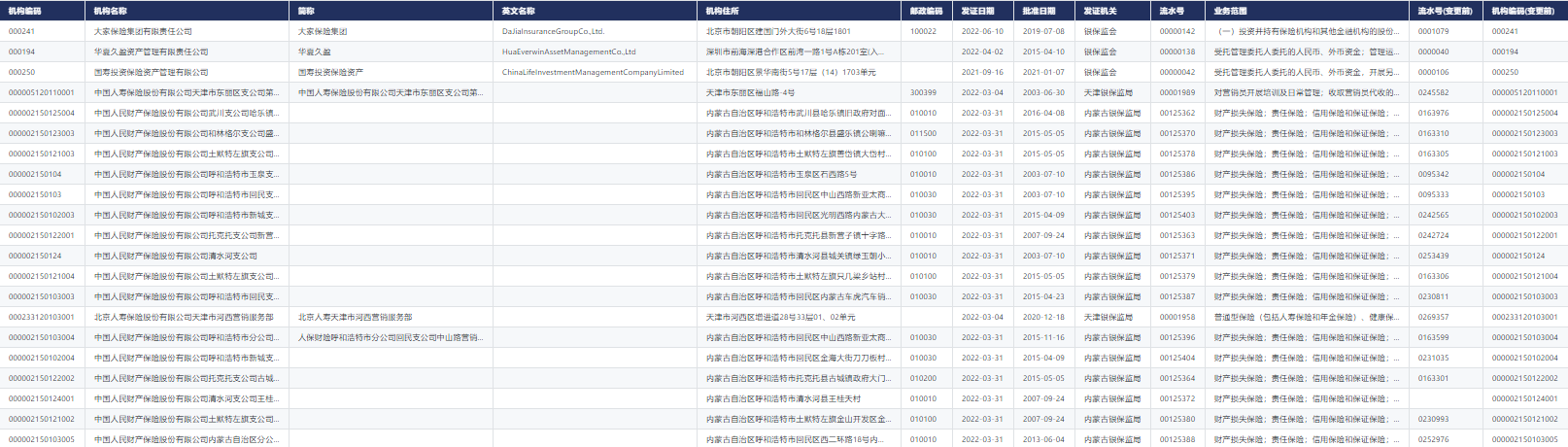
新库上线 | CnOpenData中国保险机构网点全集数据

设计电商秒杀
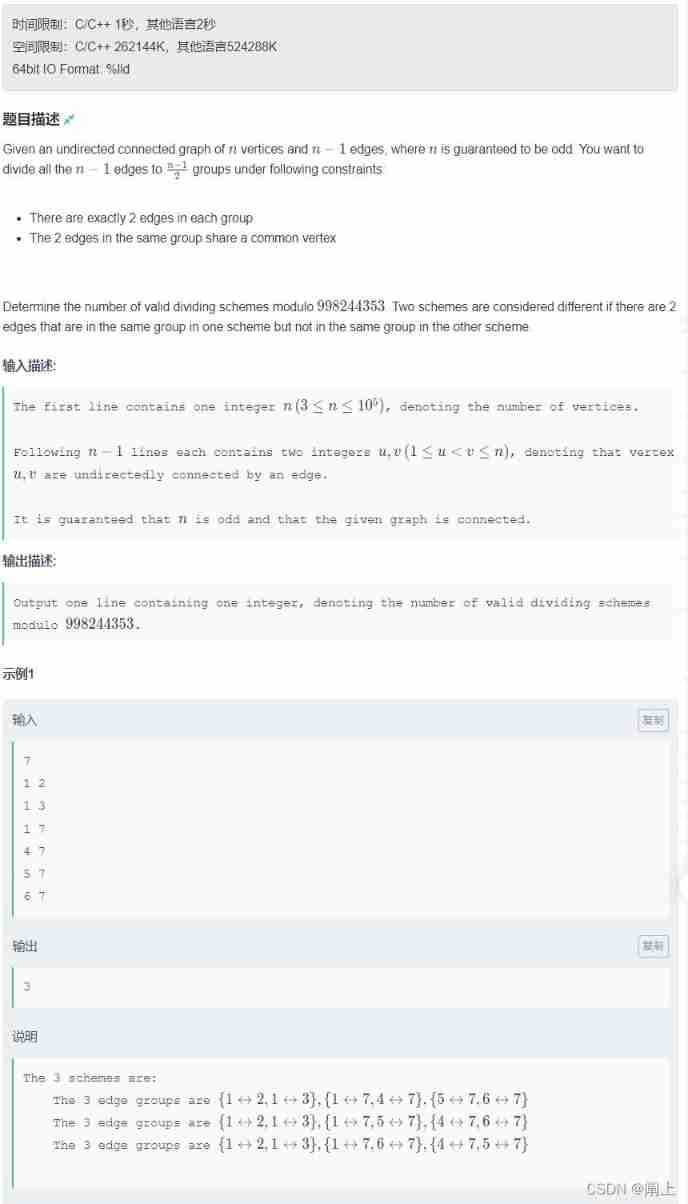
2021 ICPC regional competition (Shanghai) g.edge groups (tree DP)

QT learning diary 9 - dialog box

PHP online confusion encryption tutorial sharing + basically no solution

国内如何购买Google Colab会员

Design e-commerce spike
随机推荐
RDS数据库的监测页面在哪看?
POM in idea XML graying solution
Define a structure fraction to represent a fraction, which is used to represent fractions such as 2/3 and 5/6
When absolutely positioned, the element is horizontally and vertically centered
Y is always discrete and can't understand, how to solve it? Answer: read it several times
How to train mask r-cnn model with your own data
Swm32 series Tutorial 4 port mapping and serial port application
kubernetes资源对象介绍及常用命令(五)-(NFS&PV&PVC)
Web-ui automated testing - the most complete element positioning method
UE4 official charging resources, with a total price of several thousand
What is the difference between cloud server and cloud virtual machine
[RT thread] NXP rt10xx device driver framework -- Audio construction and use
Online assignment 3 of mobile Internet technology in the 20th autumn of electronic technology [standard answer]
[combinatorics] recursive equation (four cases where the non-homogeneous part of a linear non-homogeneous recursive equation with constant coefficients is the general solution of the combination of po
新库上线 | CnOpenData中国保险机构网点全集数据
c# .net 工具生态
How to purchase Google colab members in China
The difference between i++ and ++i: tell their differences easily
Hongmeng fourth training
The largest matrix (H) in a brush 143 monotone stack 84 histogram