当前位置:网站首页>无序数组排序并得到最大间隔
无序数组排序并得到最大间隔
2022-08-02 14:01:00 【Ethan_199402】
问题描述
给定一个无序整型数组,求将其排好序后,并得出相邻两个数之间的最大差值。
例如:{1,3,2,5,7,4,13}
排序后{1,2,3,4,5,7,13} 那么最大间隔是6
这个问题大部分人会想到先排序后遍历的解法,但是这个问题要求的时间复杂度是O(n)传统的排序并做不到
解法思路一:运用计数排序的思想
- 先求出原数组的最大值Max与最小值Min的区间长度k(k=Max-Min+1)。
- 创建一个长度为k的新数组Array。
- 遍历原数组,把原数组每一个元素插入到新数组Array对应的位置,比如元素的值为n,则插入到Array[n-min]当中。此时Array的部分位置为空,部分位置填充了数值。
- 遍历新数组Array,统计出Array中最大连续出现空值的次数+1,即为相邻元素最大差值。
public static int countSort(int[] nums) {
if (nums == null || nums.length < 2) {
return 0;
}
int maxInterval = 0;
int max = Integer.MIN_VALUE;
int min = Integer.MAX_VALUE;
int len = nums.length;
//保存原数组最大值和最小值
for (int i = 0; i < len; i++) {
max = Math.max(max, nums[i]);
min = Math.min(min, nums[i]);
}
//新数组长度区间
int[] newNums = new int[max - min + 1];
int bucketIndex = 0;
for (int i = 0; i < len; i++) {
bucketIndex = (nums[i] - min);
newNums[bucketIndex] = nums[i];
}
int lastMaxBucketValue = 0;
for (int i = 1; i < newNums.length; i++) {
//统计出Array中最大连续出现空值的次数
if (newNums[i] == 0) {
lastMaxBucketValue++;
if (lastMaxBucketValue > maxInterval) {
maxInterval = lastMaxBucketValue;
}
} else {
lastMaxBucketValue = 0;
}
}
//maxInterval+1即为所求
return maxInterval + 1;
}
但是当最大值和最小值相差巨大的时候,浪费了极大的空间,所以我们还要了解解法二
解法思路二:运用桶排序的思想
- 先求出原数组从最小值Min到最大值Max的单位区间长度d,d=(Max-Min+n+1)/n(此处运用(a+b+1)/b来获得a/b向上取整的结果)。算出d的作用是为了后续确定各个桶的区间范围划分。
- 创建一个长度是N+1的数组Array,数组的每一个元素都是一个List,代表一个桶。
- 遍历原数组,把原数组每一个元素插入到新数组Array对应的桶当中,进入各个桶的条件是根据不同的数值区间。由于桶的总数量是N+1,所以至少有一个桶是空的。
- 遍历新数组Array,计算每一个空桶右端非空桶中的最小值,与空桶左端非空桶的最大值的差,数值最大的差即为原数组排序后的相邻最大差值。(因为还要对每个桶排序才能得到最大值或者最小值,考虑到桶内排序的复杂度,我们可以做两个新数组,一个保存每个桶的最大值,一个保存每个桶的最小值,这样就免去了桶内排序的复杂度提升)
public static int bucketSort( int[] nums){
if(nums == null || nums.length < 2)
return 0;
int maxInterval = 0;
int max = Integer.MIN_VALUE;
int min = Integer.MAX_VALUE;
int len = nums.length;
//保存原数组最大值和最小值
for(int i = 0;i < len;i ++ ){
max = Math.max(max,nums[i]);
min = Math.min(min,nums[i]);
}
int[] maxs = new int[len + 1];
int[] mins = new int[len + 1];
int bucketIndex = 0;
for(int i = 0;i < len;i ++ ){
bucketIndex = (nums[i] - min) / ((max - min + len + 1)/len);
maxs[bucketIndex] = maxs[bucketIndex] == 0 ? nums[i] : Math.max(maxs[bucketIndex],nums[i]);
mins[bucketIndex] = mins[bucketIndex] == 0 ? nums[i] : Math.min(mins[bucketIndex],nums[i]);
}
int lastMaxBucketValue = maxs[0];
for(int i = 1;i < len + 1;i ++){
//获得当前非空桶最小值与上一个非空桶最大值的差值即为所求
if(mins[i] != 0){
maxInterval = Math.max(maxInterval,mins[i] - lastMaxBucketValue);
lastMaxBucketValue = maxs[i];
}
}
return maxInterval;
}
边栏推荐
- RKMPP API安装使用总结
- 面试官:可以谈谈乐观锁和悲观锁吗
- Selenium本地打开远程浏览器
- 智能指针-使用、避坑和实现
- How to do short video food from the media?5 steps to teach you to get started quickly
- Word | 关于删除分节符(下一页)前面的版式就乱了解决方案
- Shell脚本完成pxe装机配置
- ZABBIX配置邮件报警和微信报警
- 基于深度学习的图像检索方法!
- Break the limit of file locks and use storage power to help enterprises grow new momentum
猜你喜欢

玉溪卷烟厂通过正确选择时序数据库 轻松应对超万亿行数据

定了!就在7月30日!
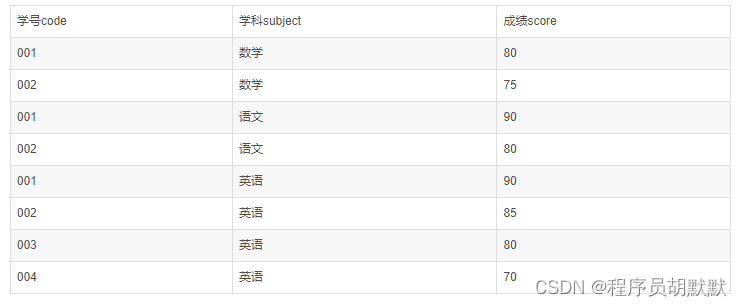
面试SQL语句,学会这些就够了!!!

第二届中国Rust开发者大会(RustChinaConf 2021~2022)线上大会正式开启报名

专访|带着问题去学习,Apache DolphinScheduler 王福政

劲爆!阿里巴巴面试参考指南(嵩山版)开源分享,程序员面试必刷
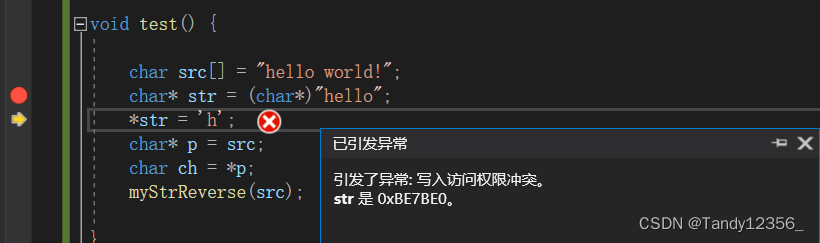
C language improvement (3)

CVE-2020-27986 (Sonarqube sensitive information leak) vulnerability fix
![[C language] Analysis of function recursion (3)](/img/95/8bd4483cf03db2dc326eb44675bf5a.png)
[C language] Analysis of function recursion (3)

如何选择正规的期货交易平台开户?
随机推荐
Why does a four-byte float represent a wider range than an eight-byte long
Fabric.js 动态设置字号大小
static修饰的函数有什么特点(static可以修饰所有的变量吗)
WiFi Association & Omnipeek Packet Capture Analysis
Detailed explanation of stored procedures
矩阵中的路径
tinymce-plugins
LeetCode(剑指 Offer)- 53 - II. 0~n-1中缺失的数字
eclipse连接数据库后插入数据报错null
世界上最大的开源基金会 Apache 是如何运作的?
关于C#使用DateTime数据的细节
面试官:可以谈谈乐观锁和悲观锁吗
Flashback Technology of Oracle Database
社区收藏缓存设计重构实战
网络安全第五次作业
二叉树的类型、构建、遍历、操作
苹果,与Web3 “八字不合”
网络安全第一次作业(2)
Flutter 实现光影变换的立体旋转效果
网络安全第一次作业