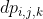当前位置:网站首页>双目立体视觉笔记(二)
双目立体视觉笔记(二)
2022-08-04 12:29:00 【郑学长】
系统校准
为了能利用立体视觉系统的视差计算三维深度信息,必须首先设法得到立体视觉系统的以下信息:
(1)相机的内部参数。包括各相机的焦距、光心及畸变模型等。
(2)相机的外部参数。包括各相机坐标系与世界坐标系之间的旋转和平移关系。
(3)相机间的相对位置关系。包括各个相机坐标系与其他相机坐标系之间的旋转和平移关系,以及多幅图像中同源像点所对应空间点的坐标等。
投影模型
在实际工程实践当中,将获取上述各种信息的过程称为对立体视觉系统的校准(Stereo Calibration)过程。为实现对立体视觉系统的校准,通常会让立体视觉系统的各个相机对同一校准点阵进行图像采集,然后根据点阵信息计算各种参数。
**双目立体视觉系统的校准过程分为相机校准和立体视觉系统校准两个阶段。**相机校准阶段会计算系统中每个相机的焦距、光心位置、相机的畸变模型,以及每个相机坐标系与世界坐标系之间的关系。单个相机校准过程实际上是确定大小为3*4投影矩阵 M M M的过程,若投影矩阵的每一项用 m i j ( i = 1 , 2 , 3 , j = 1 , 2 , 3 , 4 ) m_{ij}(i=1,2,3,j=1,2,3,4) mij(i=1,2,3,j=1,2,3,4)表示,则有
Z c [ i j 1 ] = [ m 11 m 12 m 13 m 14 m 21 m 22 m 23 m 24 m 31 m 32 m 33 m 34 ] [ X w Y w Z w 1 ] Z_{c}\begin{bmatrix}i \\j \\1 \end{bmatrix}= \begin{bmatrix}m_{11} &m_{12} &m_{13} &m_{14} \\m_{21} &m_{22} &m_{23} &m_{24} \\m_{31} &m_{32} &m_{33} &m_{34} \end{bmatrix}\begin{bmatrix}X_{w} \\Y_{w} \\Z_{w} \\1 \end{bmatrix} Zc⎣⎡ij1⎦⎤=⎣⎡m11m21m31m12m22m32m13m23m33m14m24m34⎦⎤⎣⎢⎢⎡XwYwZw1⎦⎥⎥⎤
若已知 k k k个投影前后的点对坐标 P w ( X w , Y w , Z w ) P_{w}(X_{w},Y_{w},Z_{w}) Pw(Xw,Yw,Zw)和 p ( i , j ) p(i,j) p(i,j),则可得到 k k k个方程组,第 k k k个方程组结构如下:
{ Z c k ⋅ i k = m 11 X w k + m 12 Y w k + m 13 Z w k + m 14 Z c k ⋅ j k = m 21 X w k + m 22 Y w k + m 23 Z w k + m 24 Z c k = m 31 X w k + m 32 Y w k + m 33 Z w k + m 34 \begin{cases}Z_{c}^{k} \cdot i^{k}=m_{11}X_{w}^{k}+m_{12}Y_{w}^{k}+m_{13}Z_{w}^{k}+m_{14} \\ \\Z_{c}^{k} \cdot j^{k}=m_{21}X_{w}^{k}+m_{22}Y_{w}^{k}+m_{23}Z_{w}^{k}+m_{24} \\ \\Z_{c}^{k} =m_{31}X_{w}^{k}+m_{32}Y_{w}^{k}+m_{33}Z_{w}^{k}+m_{34} \end{cases} ⎩⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎧Zck⋅ik=m11Xwk+m12Ywk+m13Zwk+m14Zck⋅jk=m21Xwk+m22Ywk+m23Zwk+m24Zck=m31Xwk+m32Ywk+m33Zwk+m34
所有 k k k个点对构成的方程组一共有 12 + k 12+k 12+k个未知量和 3 k 3k 3k个方程,要求解这些未知量,就要 3 k ≥ 12 + k 3k\ge12+k 3k≥12+k,即 k ≥ 6 k\ge6 k≥6,也就是说,若要通过投影前后的点对来计算投影矩阵 M M M,需要至少6个校准点。在实际应用中,通常使用了十几个或更多的特征点基于最小二乘法来减少可能的误差。
注意,投影矩阵和单应矩阵(Homography Matrix)是两个不同的概念。
投影矩阵用于表示三维空间点到二维图像点之间的变换关系,而单应矩阵则是指二维平面点之间的映射关系。
例如,单个相机从一角度拍摄空间某平面,该平面上的点 X = ( x , y , z ) T X=(x,y,z)^{T} X=(x,y,z)T的像点的齐次坐标为 P = ( u , v , 1 ) T P=(u,v,1)^{T} P=(u,v,1)T,若大小为 3 × 3 3\times3 3×3的矩阵 H H H能使 P = H ⋅ X P=H\cdot X P=H⋅X成立,则称 H H H为平面到成像平面的单应矩阵。再如,两个相机或相机从两个不同视角拍摄平面得到的图像分别为 I 1 和 I 2 I_{1}和I_{2} I1和I2空间平面上的点 X = ( x , y , z ) T X=(x,y,z)^{T} X=(x,y,z)T在图像上对应的投影点分别为 P 1 = ( u 1 , v 1 , 1 ) T P_{1}=(u_{1},v_{1},1)^{T} P1=(u1,v1,1)T和 P 2 = ( u 2 , v 2 , 1 ) T P_{2}=(u_{2},v_{2},1)^{T} P2=(u2,v2,1)T,若矩阵 H H H使得 P 2 = H ⋅ P 1 P_{2}=H\cdot P_{1} P2=H⋅P1成立,则称 H H H为图像 I 1 I_{1} I1和 I 2 I_{2} I2关于空间平面的单应矩阵。由于只关心空间平面坐标系(即x,y构成的平面)内点的坐标与另一平面坐标系内对应点之间的关系,因此可通过4个点对计算出单应矩阵(z可被消去)。这也是可以最少使用4个平面点阵进行畸变校准的原因。
如前面所述,表示三维空间点与图像点变换关系的投影矩阵 M M M可以通过6个以上的校准点计算得到。而基于它和相机内外参数矩阵的关系,能计算得到相机的内外参数。此后,就可以继续对整个立体视觉系统进行校准,来确定系统中各个相机的坐标系与其他相机坐标系之间的旋转和平移关系,以及多幅图像中同源点所对应空间点的坐标等。
设双目立体视觉系统中左右相机坐标系相对世界坐标系的旋转和平移矩阵分为 ( R L 、 B L ) (R_L、B_L) (RL、BL)和 ( R R , B R ) (R_R,B_R) (RR,BR),则三维世界坐标系中的点 P ( X w , Y w , Z w ) P(X_w,Y_w,Z_w) P(Xw,Yw,Zw)在两个相机坐标系中的坐标 P L ( X L , Y L , Z L ) P_L(X_L,Y_L,Z_L) PL(XL,YL,ZL)和 P R ( X R , Y R , Z R ) P_R(X_R,Y_R,Z_R) PR(XR,YR,ZR)可通过坐标旋转和平移得到。用矩阵表示为:
P L = R L P + B L , P R = R R P + B R P_L=R_LP+B_L, P_R=R_RP+B_R PL=RLP+BL,PR=RRP+BR.
消去 P P P可得到以下 P L P_L PL和 P R P_R PR之间的关系式:
P L = R P R + B P_L=RP_R+B PL=RPR+B
R = R L R R − 1 R=R_LR_R^{-1} R=RLRR−1
B = B L − R L R R − 1 B R B=B_L-R_LR_R^{-1}B_R B=BL−RLRR−1BR
由上式可知,若对双目立体视觉系统中的左右相机分别完成标定得到 ( R L , B L ) (R_L,B_L) (RL,BL)和 ( R R , B R ) (R_R,B_R) (RR,BR),则左相机坐标系到右相机坐标系的转换关系就能通过 R = ( R L R R − 1 ) R=(R_LR_R^{-1}) R=(RLRR−1)和 B = ( B L − R L R R − 1 B R ) B=(B_L-R_LR_R^{-1}B_R) B=(BL−RLRR−1BR)来确定。然而在实际中,通常并不会根据空间点和各成像点之间的关系来间接计算立体视觉系统中相机之间的相对位置,而是基于极线几何理论,设法直接得到两个相机图像中对应点的极线约束,然后才完成后续的立体视觉图像调整(Stereo Image Rectification)、图像对应点匹配(Stereo Image Correspondence)和目标的深度信息计算等过程。
对极几何
极线几何理论可用于研究立体视觉系统各个相机图像中,同源像点之间的关系,它不仅在双目立体视觉图像的对应点匹配有着重要通,而且在三维重建和运动分析中也具有广泛应用。立体视觉系统中的极线几何常涉及以下几个关键的定义
(1)基线(Baseline):指左右两摄像机光心的连线。
(2)极平面(Epipolar Plane):指三维空间点 P ( X w , Y w , Z w ) P(X_w,Y_w,Z_w) P(Xw,Yw,Zw)与两摄像机光心 O L O_L OL和 O R O_R OR所确定的平面。
(3)极点(Epipolar Point):指基线与两摄像机图像平面的交点,如图 1中的 E L E_L EL和 E R E_R ER。
(4)极线(Epipolar Line):指极平面与图像平面的交线,如图中 p ( u L , v L ) p(u_L,v_L) p(uL,vL)和 E L E_L EL、 p ( u R , v R ) p(u_R,v_R) p(uR,vR)和 E R E_R ER之间的线段,称“线段 p ( u R , v R ) — — E R p(u_R,v_R)——E_R p(uR,vR)——ER”为点 p ( u R , v R ) p(u_R,v_R) p(uR,vR)的极线。称“线段 p ( u L , v L ) — — E L p(u_L,v_L)——E_L p(uL,vL)——EL”为点 p ( u L , v L ) p(u_L,v_L) p(uL,vL)的极线。同一图像平面内所有的极线交于极点。
(5)极平面簇(Epipolar Plane Cluster):由基线和空间任意一点确定的一簇平面,它们均相交于基线。如图 2所示,点 P P P与 P ′ P^{'} P′与基线所确定的平面相交于基线。
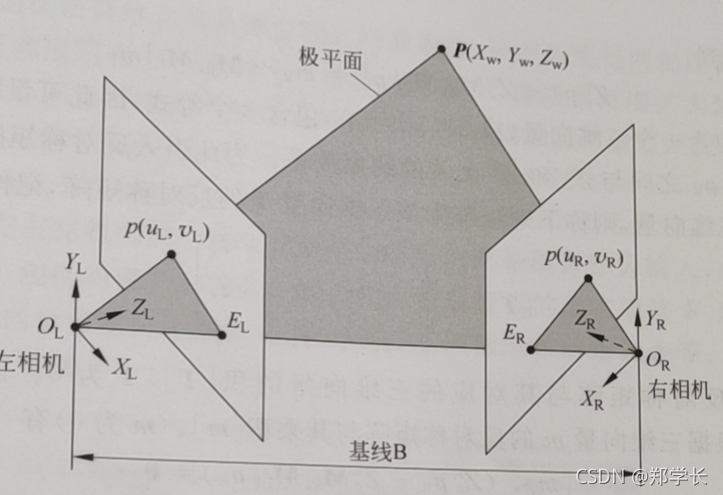
图 1 双目立体视觉系统中的对极几何
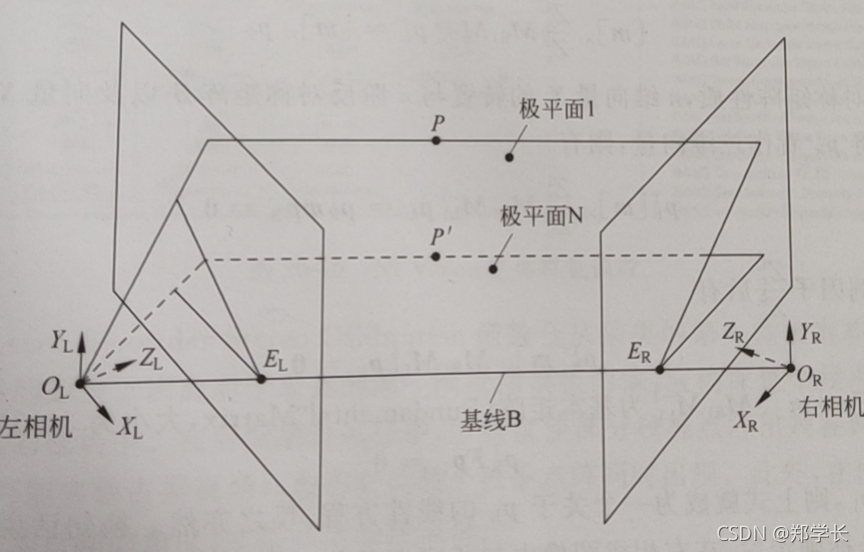
图 2 极平面簇
由以上定义可知,若已知点 p ( u L , v L ) p(u_{L},v_{L}) p(uL,vL)在左图像内的坐标,则右图像内与其同源的像点 p ( u R , v R ) p(u_R,v_R) p(uR,vR)必定位于 p ( u L , v L ) p(u_L,v_L) p(uL,vL)的极线“线段 p ( u L , v L ) — — E L p(u_L,v_L)——E_L p(uL,vL)——EL”上,反之亦然。双目立体视觉系统的这一个重要特点称为极线约束。为了寻找极线约束的数学关系式,根据上节讨论,不妨将左右相机模型用投影矩阵M表达为:
{ Z c L p L = M L ⋅ P w ′ Z c R p R = M R ⋅ P w ′ \begin{cases}Z_{c}^{L}p_{L}=M_{L} \cdot P_{w}^{'} \\Z_{c}^{R}p_{R}=M_{R} \cdot P_{w}^{'} \end{cases} { ZcLpL=ML⋅Pw′ZcRpR=MR⋅Pw′
其中 p L p_L pL和 p R p_R pR是空间点 P w ( X w , Y w , Z w ) P_w(X_{w},Y_{w},Z_{w}) Pw(Xw,Yw,Zw)在左右图像中像点 p L ( i , j ) p_{L}(i,j) pL(i,j)和 p R ( i , j ) p_{R}(i,j) pR(i,j)的齐次坐标, M L M_{L} ML和 M R M_{R} MR为左右相机的投影矩阵, P w ′ P_{w}^{'} Pw′是空间点 P w ( X w , Y w , Z w ) P_{w}(X_{w},Y_{w},Z_{w}) Pw(Xw,Yw,Zw)的齐次坐标, Z c L Z_{c}^{L} ZcL和 Z c R Z_{c}^{R} ZcR分别为左右相机系统的比例因子。若将大小为 3 × 4 3 \times 4 3×4的两个矩阵 M L M_{L} ML和 M R M_{R} MR中左面的 3 × 3 3 \times 3 3×3部分分别记作 M L 1 M_{L1} ML1和 M R 1 M_{R1} MR1,右边的 3 × 1 3 \times 1 3×1部分分别记作 m L m_{L} mL和 m R m_{R} mR,并且将 P w ′ P_{w}^{'} Pw′表示为 P w ′ = ( P w T , 1 ) T P_{w}^{'}=(P_{w}^{T} ,1)^{T} Pw′=(PwT,1)T,则有:
{ Z c L p L = M L 1 ⋅ P w + m L Z c R p R = M R 1 ⋅ P w + m R \begin{cases}Z_{c}^{L}p_{L}=M_{L1} \cdot P_{w}+m_L{} \\Z_{c}^{R}p_{R}=M_{R1} \cdot P_{w}+m_{R} \end{cases} { ZcLpL=ML1⋅Pw+mLZcRpR=MR1⋅Pw+mR
消去 P w P_{w} Pw后可得到:
Z c R p R − Z c L M R 1 M L 1 − 1 p L = m R − M R 1 M L 1 − 1 m L Z_{c}^{R}p_{R}-Z_{c}^{L}M_{R1}M_{L1}^{-1}p_{L}=m_{R}-M_{R1}M_{L1}^{-1}m_{L} ZcRpR−ZcLMR1ML1−1pL=mR−MR1ML1−1mL,
上式两边均为一个三维向量,则称下列矩阵为该三维向量 T T T的反对称矩阵,记作 [ T ] × [T]_{\times} [T]×:
[ T ] × = [ 0 − t z t y t z 0 − t x − t y t x 0 ] [T]_{\times}=\begin{bmatrix}0 &-t_{z} &t_{y} \\t_{z} &0 &-t_{x} \\-t_{y} &t_{x} &0 \end{bmatrix} [T]×=⎣⎡0tz−ty−tz0txty−tx0⎦⎤
不难看出,反对称矩阵与其对应的三维向量的积 [ T ] x T [T]_{x}T [T]xT为0.由此令 m = m R − M R 1 M L 1 − 1 m L m=m_{R}-M_{R1}M_{L1}^{-1}m_{L} m=mR−MR1ML1−1mL,则根据三维向量 m m m的反对称矩阵与其乘积 [ m ] x [m]_{x} [m]x(m为0)有
[ m ] × ( Z c R p R − Z c L M R 1 M L 1 − 1 p L ) = 0 \mathbf{[m]_{\times}(Z_{c}^{R}p_{R}-Z_{c}^{L}M_{R1}M_{L1}^{-1}p_{L})=0} [m]×(ZcRpR−ZcLMR1ML1−1pL)=0
两边除以 Z c R \mathbf{Z_{c}^{R}} ZcR并移项后有
[ m ] × ⋅ Z c L Z c R ⋅ M R 1 ⋅ M L 1 − 1 ⋅ p L = [ m ] × ⋅ p R \mathbf{[m]_{\times} \cdot \frac{Z_{c^{L}}}{Z_{c}^{R}} \cdot M_{R1} \cdot M_{L1}^{-1} \cdot p_{L}=[m]_{\times} \cdot p_{R}} [m]×⋅ZcRZcL⋅MR1⋅ML1−1⋅pL=[m]×⋅pR
根据反对称矩阵性质,n维列向量 X X X的转置与n阶反对称矩阵 B B B以及向量 X X X的积 X T B X X^{T}BX XTBX等于0。若将 p R p_{R} pR看作三维向量,则有:3
p R T ⋅ [ m ] × ⋅ Z c L Z c R ⋅ M R 1 ⋅ M L 1 − 1 ⋅ p L = p R T ⋅ m ⋅ p R = 0 \mathbf{p_{R}^{T} \cdot [m]_{\times} \cdot \frac{Z_{c^{L}}}{Z_{c}^{R}} \cdot M_{R1} \cdot M_{L1}^{-1} \cdot p_{L}=p_{R}^{T} \cdot m \cdot p_{R} = 0} pRT⋅[m]×⋅ZcRZcL⋅MR1⋅ML1−1⋅pL=pRT⋅m⋅pR=0
消去比例因子 Z c L Z c R \frac {Z_{c}^{L}}{Z_{c}^{R}} ZcRZcL后有:
p R T ⋅ [ m ] × ⋅ M R 1 M L 1 − 1 p L = 0 p_{R}^{T} \cdot [m]_{\times} \cdot M_{R1}M_{L1}^{-1}p_{L}=0 pRT⋅[m]×⋅MR1ML1−1pL=0
若定义 F = [ m ] × ⋅ M R 1 M L 1 − 1 F=[m]_{\times} \cdot M_{R1} M_{L1}^{-1} F=[m]×⋅MR1ML1−1为基本矩阵(Fundamental Matrix,大小为3*3),则有: p R T F p L = 0 p_{R}^{T}Fp_{L}=0 pRTFpL=0
若给定 p L p_{L} pL,则上式就成为一个关于 p R p_{R} pR的线性方程,反之亦然。换句话说,当左相机图像中的像点坐标确定后,在右相机图像中与其同源的像点将落在由基本矩阵所确定的直线上。这说明采用基本矩阵可以通过以下公式来表示极线约束:
对应左像点的右极线: l R = F p L \mathbf l_{R}=Fp_{L} lR=FpL
对应右像点的左极线: l L = F T p R \mathbf l_{L}=F^{T}p_{R} lL=FTpR
由于基本矩阵包含了左右图像中对应像素坐标之间的转换关系,因此它实际上是对立体视觉系统中相机的内外参数和相机的相对位置信息的综合。若已知立体视觉系统中相机的内部参数矩阵,还能在约束条件 p R T F p L = 0 \mathbf{p_{R}^{T}Fp_{L}=0} pRTFpL=0的基础上,得到位于相机坐标系中的两个同源像点 P L ( X L , Y L , Z L ) P_{L}(X_{L},Y_{L},Z_{L}) PL(XL,YL,ZL)和 P R ( X R , Y R , Z R ) P_{R}(X_{R},Y_{R},Z_{R}) PR(XR,YR,ZR)之间的约束关系: p R T ⋅ E ⋅ P L = 0 \mathbf{p_{R}^{T} \cdot E \cdot P_{L}=0} pRT⋅E⋅PL=0
其中矩阵 E \mathbf{E} E称为本质矩阵(Essential Matrix),大小为3*3.本质矩阵实际上描述左右相机坐标系之间的旋转和平移关系。它只与相机之间的相对位置有关,与各个相机自身的焦距、光心和传感器像素大小等内部参数无关。因此,它仅适用于两个相机坐标系中的同源像点的物理坐标系转换,而不能在它们的图像像素坐标系之间建立联系。
总结
由上述几何和数学分析可见,极线约束表示的是像点与其极线之间的约束关系,通过这种约束关系,可得到一个相机图像内某一像点在另一相机图像中位置所在的直线,而不能确切知道同源像点的在该直线上的具体位置。尽管如此,极限约束将两幅图像内对应点的匹配范围,从整幅图像限定在一条直线上。即使考虑噪声,将搜索范围扩大到该直线的邻域内,也能极大地减少图像对应点匹配过程中的计算量,因此对图像对应点匹配具有指导作用。
边栏推荐
猜你喜欢
随机推荐
大神们都在用的神器,你和大神只差一个它!!
Flutter教程大全合集(2022年版)
飞书更新招聘功能 候选人可选择面试时间
分布式链路追踪Jaeger + 微服务Pig在Rainbond上的实践分享
Flutter强大的下拉筛选菜单gzx_dropdown_menu
关于mysql join 的一些说明
持续交付(四)Jenkins多线程任务执行
Js获取当前页面url参数
简要介绍电源效率测试
【Game Of AutoTest】1、再度启程,重识游戏自动化测试
手搓一个“七夕限定”,用3D Engine 5分钟实现烟花绽放效果
ES 节点2G内存分析
[牛客网]OR63删除公共字符
动规(16)-并查集基础题——格子游戏
“蔚来杯“2022牛客暑期多校训练营2 G、J、K
全面认识MOS管,一篇文章就够了
DateTimeFormatter api
拥有一台服务器,程序猿装X的开始
Cache character stream
常用代码模板1——基础语法