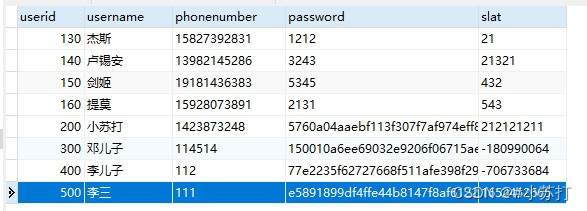
当前位置:网站首页>Bolb analysis of image processing (1)
Bolb analysis of image processing (1)
2022-08-04 04:30:00 【Schrodinger cat】
文章目录
前言
Bolb分析,connected domain analysis.Out-of-the-box open source libraries areOpenCV中的SimpleBlobDetector类、findContours,以及skimage.measue的regionprops等.这里介绍skimage.measue的regionprops.
skimage中的regionprops
regionprops
以skimage 0.19.1为例:
源码位置:https://github.com/scikit-image/scikit-image/blob/main/skimage/measure/_regionprops.py
regionprops函数
def regionprops(label_image, intensity_image=None, cache=True,
coordinates=None, *, extra_properties=None):
r"""Measure properties of labeled image connected domains. Parameters ---------- label_image : (M, N[, P]) ndarray input label image. 0标签忽略 intensity_image : (M, N[, P][, C]) ndarray, optional Intensity image the same size as the label image, 可选参数. Optional extra dimension for multi-channel data.目前,This additional channel size,如果存在,must be the last axis.默认是None cache : bool, optional Determines whether computed properties are cached.Calculation of cached properties is much faster,But memory consumption will increase. coordinates : DEPRECATED This argument is deprecated and will be removed in a future version of scikit-image. extra_properties : Iterable of callables 添加skimageAdditional property calculation functions not found in.The property name and function name are the same as the function name,dtypeis inferred by calling the function on a small sample. If the name of an extra property conflicts with the name of an existing property, the extra property will not be visible,并使用UserWarning警告. A property calculation function must accept a region mask as its first argument.If the property requires an intensity image,It must accept an intensity image as the second parameter. Returns ------- properties : list of RegionProperties Connected Domain Attribute List,Available properties are in the next section """
Properties and data types
{
#********几何特征********#
'area': int, # 连通域面积
'area_bbox': int, # 外接矩形面积
'area_convex': int, # Minimum convex hull area
'area_filled': int, # Hole filling area
'axis_major_length': float, # 长轴 The second central moment and connected domain with the same standard of the long axis of the ellipse
'axis_minor_length': float, # 短轴
'bbox': int, # 边界框,That is, the coordinates of the circumscribed rectangle (min_row, min_col, max_row, max_col)
'centroid': float, # 质心坐标 (row, col)
'centroid_local': float, # 质心-局部坐标
'centroid_weighted': float, # Centroid coordinates weighted using intensity image
'centroid_weighted_local': float,# Centroids weighted using intensity images-局部坐标
'eccentricity': float, # 偏心率 The eccentricity of an ellipse with the same second order central moment as the connected domain.公式:焦距c/长轴a [0, 1),0round.
'equivalent_diameter_area': float, # 等效直径 the diameter of the circle with the same area as the connected domain
'euler_number': int, # 欧拉数 Euler features of non-zero pixel sets.公式:连通域数目 - number of holes.3D里面:连通域数目*number of holes-number of tunnels
'extent': float, # 范围 连通域面积/外接矩形面积 area / (rows * cols)
'feret_diameter_max': float, # 最大Feret直径,passed by calculationfind_contoursGet connected domain of the longest distance between convex hull contour points
'orientation': float, # The ellipse with the same second moment as the connected domain0轴(rows)Angle with the main axis,从' -pi/2 '到' pi/2 ',逆时针方向.
'perimeter': float, # Connected domain circumference,Its contour is approximated as a line passing through the center of the boundary contour pixel,使用4连通分析.
'perimeter_crofton': float, # Approximate the perimeter of an object using Crofton's formula in four directions.
'solidity': float, # Ratio of connected domain pixels to convex hull pixels
#********连通域********#
'slice': object, # Extract slices of objects from source images.
'coords': object, # the coordinates of the connected domain (N, 2) ndarray
'image': object, # Binary region image slice of the same size as the bounding box
'image_convex': object, # With the bounding box binary convex hull image with the same size.
'image_filled': object, # Binary image of filled holes the same size as the bounding box
#********灰度特征********#
'intensity_max': float, # Connected Domain Strength Maximum(The intensity image corresponding to the binary image needs to be provided)
'intensity_mean': float, # Connected Domain Strength Mean
'intensity_min': float, # The intensity of connected domain the minimum value
'label': int, # Labeling connected domains in an imagelabel
#********矩特征********#
'image_intensity': object, # The strength of the boundary frame image
'inertia_tensor': float, # Connected Domain Region Inertia Tensor Rotating Around Mass.
'inertia_tensor_eigvals': float, # Inertia tensor eigenvalues,按降序排列
'moments': float, # third-order space moments m_ij = sum{ array(row, col) * row^i * col^j },其中sumSum on connected domain ranks (3, 3) ndarray
'moments_central': float, # Central moment of third order(平移不变), mu_ij = sum{ array(row, col) * (row - row_c)^i * (col - col_c)^j },' row_c '和' col_c 'is the coordinate barycenter of the connected domain.
'moments_hu': float, # hu矩(平移、Scale and rotation invariants).
'moments_normalized': float, # third-order normalizing moments(Pan and zoom unchanged) nu_ij = mu_ij / m_00^[(i+j)/2 + 1], 其中m_00is the zeroth order space moment
'moments_weighted': float, # third-order spatial moments of the intensity image,wm_ij = sum{ array(row, col) * row^i * col^j },其中sumSum on connected domain ranks
'moments_weighted_central': float, # The third order central spatial moment of the intensity image, wmu_ij = sum{ array(row, col) * (row - row_c)^i * (col - col_c)^j },其中sumSum on connected domain ranks, ' row_c '和' col_c 'is the barycenter of the coordinates weighted by the connected domain.
'moments_weighted_hu': float, # third order of intensity imagehu矩(平移、Scale and rotation invariants)
'moments_weighted_normalized': float,# third-order normalized moments of the intensity image(Pan and zoom unchanged) wnu_ij = wmu_ij / wm_00^[(i+j)/2 + 1],:“wm_00”是0zero-order space moment(Intensity weight area)
}
References
[1] Wilhelm Burger, Mark Burge. Principles of Digital Image Processing:
Core Algorithms. Springer-Verlag, London, 2009.
[2] B. Jähne. Digital Image Processing. Springer-Verlag,
Berlin-Heidelberg, 6. edition, 2005.
[3] T. H. Reiss. Recognizing Planar Objects Using Invariant Image
Features, from Lecture notes in computer science, p. 676. Springer,
Berlin, 1993.
[4] https://en.wikipedia.org/wiki/Image_moment
[5] W. Pabst, E. Gregorová. Characterization of particles and particle
systems, pp. 27-28. ICT Prague, 2007.
https://old.vscht.cz/sil/keramika/Characterization_of_particles/CPPS%20_English%20version_.pdf
源码
Here are some important source code,数据类型检测,Parameter checking and the like will not be repeated here..
regionprops函数
def regionprops(label_image, intensity_image=None, cache=True,
coordinates=None, *, extra_properties=None):
if label_image.ndim not in (2, 3): # 函数只支持2维和3维图片
raise TypeError('Only 2-D and 3-D images supported.')
if not np.issubdtype(label_image.dtype, np.integer): # Define supported data types 即integer的子类型,比如np.int16 np.uint8
if np.issubdtype(label_image.dtype, bool):
raise TypeError(
'Non-integer image types are ambiguous: '
'use skimage.measure.label to label the connected'
'components of label_image,'
'or label_image.astype(np.uint8) to interpret'
'the True values as a single label.')
else:
raise TypeError(
'Non-integer label_image types are ambiguous')
if coordinates is not None: # 坐标系 rcThe coordinate system isrow-column坐标系
if coordinates == 'rc':
msg = ('The coordinates keyword argument to skimage.measure.'
'regionprops is deprecated. All features are now computed '
'in rc (row-column) coordinates. Please remove '
'`coordinates="rc"` from all calls to regionprops before '
'updating scikit-image.')
warn(msg, stacklevel=2, category=FutureWarning)
else:
msg = ('Values other than "rc" for the "coordinates" argument '
'to skimage.measure.regionprops are no longer supported. '
'You should update your code to use "rc" coordinates and '
'stop using the "coordinates" argument, or use skimage '
'version 0.15.x or earlier.')
raise ValueError(msg)
regions = []
objects = ndi.find_objects(label_image) # Returns a slice of each connected domain 忽略0标签
for i, sl in enumerate(objects):
if sl is None:
continue
label = i + 1
props = RegionProperties(sl, label, label_image, intensity_image,
cache, extra_properties=extra_properties) # 构造RegionProperties类
regions.append(props) # regionsThere are a class
return regions
its instantiatedRegionProperties类
class RegionProperties:
"""Please refer to `skimage.measure.regionprops` for more information on the available region properties. """
# 初始化
def __init__(self, slice, label, label_image, intensity_image,
cache_active, *, extra_properties=None):
if intensity_image is not None: # Determine if there is an intensity image,Used to calculate certain properties that require an intensity image,比如intensity_max等
ndim = label_image.ndim
if not (
intensity_image.shape[:ndim] == label_image.shape
and intensity_image.ndim in [ndim, ndim + 1]
):
raise ValueError('Label and intensity image shapes must match,'
' except for channel (last) axis.')
multichannel = label_image.shape < intensity_image.shape
else:
multichannel = False
# 初始化参数
self.label = label
self._slice = slice
self.slice = slice
self._label_image = label_image
self._intensity_image = intensity_image
self._cache_active = cache_active
self._cache = {
}
self._ndim = label_image.ndim
self._multichannel = multichannel
self._spatial_axes = tuple(range(self._ndim))
self._extra_properties = {
}
if extra_properties is not None: # If there is a custom property function,Here to get the function name
for func in extra_properties:
name = func.__name__
if hasattr(self, name): # If the custom attribute function name from the built-in attribute function overlap,ignore and warn
msg = (
f"Extra property '{
name}' is shadowed by existing "
f"property and will be inaccessible. Consider "
f"renaming it."
)
warn(msg)
self._extra_properties = {
func.__name__: func for func in extra_properties
}
# 重载__getattr__函数,make some judgments
def __getattr__(self, attr):
if attr in self._extra_properties:
func = self._extra_properties[attr]
n_args = _infer_number_of_required_args(func)
# Determine if a function requires an intensity image
if n_args == 2:
if self._intensity_image is not None:
if self._multichannel:
multichannel_list = [func(self.image,
self.image_intensity[..., i])
for i in range(
self.image_intensity.shape[-1])]
return np.stack(multichannel_list, axis=-1)
else:
return func(self.image, self.image_intensity)
else:
raise AttributeError(
f'intensity image required to calculate {
attr}'
)
elif n_args == 1:
return func(self.image)
else:
raise AttributeError(
f'Custom regionprop function\'s number of arguments must '
f'be 1 or 2, but {
attr} takes {
n_args} arguments.'
)
elif attr in PROPS and attr.lower() == attr: # 为了向后兼容,some outdated names
# Retrieve deprecated properties(does not include oldCamelCase属性)
return getattr(self, PROPS[attr])
else:
raise AttributeError(
f"'{
type(self)}' object has no attribute '{
attr}'"
)
# 重载__setattr__函数,make some judgments
def __setattr__(self, name, value):
if name in PROPS:
super().__setattr__(PROPS[name], value)
else:
super().__setattr__(name, value)
area
@property
@_cached
def area(self):
return np.sum(self.image)
使用np.sum()统计连通域面积
关于装饰器@property和@_cached:
@property装饰器就是负责把一个方法变成属性调用的.是python内置装饰器
参考:https://blog.csdn.net/qq_42350970/article/details/84943534
@_cached装饰器是_reginoprops.py里面定义的,Used to determine whether the computed property is cached.
All subsequent property functions [email protected]装饰器,Used to turn the method into a property call,Some may reuse properties,有@_cached装饰器,Used to control the cache the attribute value,加快计算速度.
bbox
@property
def bbox(self):
""" Returns ------- A tuple of the bounding box's start coordinates for each dimension, followed by the end coordinates for each dimension """
return tuple([self.slice[i].start for i in range(self._ndim)] +
[self.slice[i].stop for i in range(self._ndim)])
The connected domainsliceThe slice storage format is:
((lf_top_r, rg_bot_r, None), (lf_top_c, lf_top_c, None))
So the bounding box can be directly taken out.
coords、centroid
@property
def centroid(self):
return tuple(self.coords.mean(axis=0))
The centroid is the average value of the coordinates of the connected domain.,where the function to get the coordinates of the connected domaincoords()定义如下:
@property
def coords(self):
indices = np.nonzero(self.image)
return np.vstack([indices[i] + self.slice[i].start
for i in range(self._ndim)]).T
这里np.nonzero()The obtained coordinates are local coordinates,So you need to add the coordinates of the upper left corner of the connected domain to get the global coordinates.
image_convex、area_convex
@property
@_cached
def image_convex(self):
from ..morphology.convex_hull import convex_hull_image
return convex_hull_image(self.image)
Convex Hull Image Calculation,使用了skimage.morphology.convex_hull_image函数,Specific algorithm implementation can reference:
https://github.com/scikit-image/scikit-image/blob/main/skimage/morphology/convex_hull.py
@property
@_cached
def area_convex(self):
return np.sum(self.image_convex)
area_convexConvex Hull Image Area Usenp.sum()计算
eccentricity
@property
@only2d
def eccentricity(self):
l1, l2 = self.inertia_tensor_eigvals
if l1 == 0:
return 0
return sqrt(1 - l2 / l1)
偏心率 The eccentricity of an ellipse with the same second order central moment as the connected domain.公式:焦距c/长轴a [0, 1),0round.
其使用到了inertia_tensor_eigvals()函数:
@property
@_cached
def inertia_tensor_eigvals(self):
return _moments.inertia_tensor_eigvals(self.image,
T=self.inertia_tensor)
其调用了_moments.inertia_tensor_eigvals()函数:
@property
@_cached
def inertia_tensor(self):
mu = self.moments_central
return _moments.inertia_tensor(self.image, mu)
其调用了moments_central和_moments.inertia_tensor()
而moments_central又调用了_moments.moments_central(self.image.astype(np.uint8),
self.centroid_local, order=3)
self.centroid_local调用了moments()方法,moments()调用了 _moments.moments
Therefore, the order of calculation of eccentricity is as follows::
_moments.moments # 矩
self.centroid_local # local centroid
_moments.moments_central # 中心矩
_moments.inertia_tensor # 惯性张量
_moments.inertia_tensor_eigvals # Inertia tensor eigenvalues
# Then calculate the eccentricity based on the inertia tensor eigenvalues.
About the central moment、惯性张量、Inertia tensor eigenvalue algorithm implementation can refer to:
https://github.com/scikit-image/scikit-image/blob/main/skimage/measure/_moments.py
- moments 矩
def moments(image, order=3):
"""Calculate the original moment of the image of the specified order. The following properties can be calculated from the original moments of the image: * Area as: ``M[0, 0]``. * Centroid as: {``M[1, 0] / M[0, 0]``, ``M[0, 1] / M[0, 0]``}. 注意:Image original moments are not translations、缩放、旋转不变的. Parameters ---------- image : nD double or uint8 array Rasterized shape as image. order : int, optional Maximum order of moments. Default is 3. Returns ------- m : (``order + 1``, ``order + 1``) array Raw image moments. References ---------- .. [1] Wilhelm Burger, Mark Burge. Principles of Digital Image Processing: Core Algorithms. Springer-Verlag, London, 2009. .. [2] B. Jähne. Digital Image Processing. Springer-Verlag, Berlin-Heidelberg, 6. edition, 2005. .. [3] T. H. Reiss. Recognizing Planar Objects Using Invariant Image Features, from Lecture notes in computer science, p. 676. Springer, Berlin, 1993. .. [4] https://en.wikipedia.org/wiki/Image_moment Examples -------- >>> image = np.zeros((20, 20), dtype=np.double) >>> image[13:17, 13:17] = 1 >>> M = moments(image) >>> centroid = (M[1, 0] / M[0, 0], M[0, 1] / M[0, 0]) >>> centroid (14.5, 14.5) """
return moments_central(image, (0,) * image.ndim, order=order)
其调用了moments_central
对于二维连续函数f(x,y),(p + q)阶矩(Primitive Moment)定义为:
M p q = ∫ − ∞ ∞ ∫ − ∞ ∞ x p y q f ( x , y ) d x d y M_{p q}=\int_{-\infty}^{\infty} \int_{-\infty}^{\infty} x^{p} y^{q} f(x, y) d x d y Mpq=∫−∞∞∫−∞∞xpyqf(x,y)dxdy
对于p,q = 0,1,2,…Adapt it to pixel intensities asI(x,y)的标量(灰度)图像,original image momentMij计算为:
M i j = ∑ x ∑ y x i y j I ( x , y ) M_{i j}=\sum_{x} \sum_{y} x^{i} y^{j} I(x, y) Mij=x∑y∑xiyjI(x,y)
在某些情况下,This can be calculated by considering the image as a probability density function,即,by dividing by the above
∑ x ∑ y I ( x , y ) \sum_{x} \sum_{y} I(x, y) x∑y∑I(x,y)
a uniqueness theorem(Hu[1962])指出,如果f(x,y)是分段连续的,且仅在xyhas non-zero values on finite parts of the plane,then all order moments exist,and sequence of moments(Mpq)是由f(x,y)唯一确定的.相反,(Mpq)唯一确定f(x,y).在实际应用中,The image is summed up in a few low order moment function.
Simple image properties computable by raw moments are:
面积 (for binary images)or grayscale sum(for grayscale images): M 00 M_{00} M00
中心: { x ˉ , y ˉ } = { M 10 M 00 , M 01 M 00 } \{\bar{x}, \bar{y}\}=\left\{\frac{M_{10}}{M_{00}}, \frac{M_{01}}{M_{00}}\right\} { xˉ,yˉ}={ M00M10,M00M01}
- moments_central
def moments_central(image, center=None, order=3, **kwargs):
"""Calculate all central image moments up to a certain order. The center coordinates (cr, cc) can be calculated from the raw moments as: {``M[1, 0] / M[0, 0]``, ``M[0, 1] / M[0, 0]``}. Note that central moments are translation invariant but not scale and rotation invariant. Parameters ---------- image : nD double or uint8 array Rasterized shape as image. center : tuple of float, optional Coordinates of the image centroid. This will be computed if it is not provided. order : int, optional The maximum order of moments computed. Returns ------- mu : (``order + 1``, ``order + 1``) array Central image moments. References ---------- .. [1] Wilhelm Burger, Mark Burge. Principles of Digital Image Processing: Core Algorithms. Springer-Verlag, London, 2009. .. [2] B. Jähne. Digital Image Processing. Springer-Verlag, Berlin-Heidelberg, 6. edition, 2005. .. [3] T. H. Reiss. Recognizing Planar Objects Using Invariant Image Features, from Lecture notes in computer science, p. 676. Springer, Berlin, 1993. .. [4] https://en.wikipedia.org/wiki/Image_moment Examples -------- >>> image = np.zeros((20, 20), dtype=np.double) >>> image[13:17, 13:17] = 1 >>> M = moments(image) >>> centroid = (M[1, 0] / M[0, 0], M[0, 1] / M[0, 0]) >>> moments_central(image, centroid) array([[16., 0., 20., 0.], [ 0., 0., 0., 0.], [20., 0., 25., 0.], [ 0., 0., 0., 0.]]) """
if center is None: # If no center is specified,使用1Order Primitive Moment Computation Center
center = centroid(image)
float_dtype = _supported_float_type(image.dtype)
calc = image.astype(float_dtype, copy=False)
# Start computing center moment
for dim, dim_length in enumerate(image.shape):
delta = np.arange(dim_length, dtype=float_dtype) - center[dim]
powers_of_delta = (
delta[:, np.newaxis] ** np.arange(order + 1, dtype=float_dtype)
)
calc = np.rollaxis(calc, dim, image.ndim)
calc = np.dot(calc, powers_of_delta)
calc = np.rollaxis(calc, -1, dim)
return calc
The central moment is defined as:
μ p q = ∫ − ∞ ∞ ∫ − ∞ ∞ ( x − x ˉ ) p ( y − y ˉ ) q f ( x , y ) d x d y \mu_{p q}=\int_{-\infty}^{\infty} \int_{-\infty}^{\infty}(x-\bar{x})^{p}(y-\bar{y})^{q} f(x, y) d x d y μpq=∫−∞∞∫−∞∞(x−xˉ)p(y−yˉ)qf(x,y)dxdy
其中, x ˉ = M 10 M 00 \bar{x}=\frac{M_{10}}{M_{00}} xˉ=M00M10, y ˉ = M 01 M 00 \bar{y}=\frac{M_{01}}{M_{00}} yˉ=M00M01,is the mass of the centroid
如果 f ( x , y ) f(x, y) f(x,y)is a digital image,上面的公式变为:
μ p q = ∑ x ∑ y ( x − x ˉ ) p ( y − y ˉ ) q f ( x , y ) \mu_{p q}=\sum_{x} \sum_{y}(x-\bar{x})^{p}(y-\bar{y})^{q} f(x, y) μpq=x∑y∑(x−xˉ)p(y−yˉ)qf(x,y)
The third order central moment is:
μ 00 = M 00 , μ 01 = 0 , μ 10 = 0 , μ 11 = M 11 − x ˉ M 01 = M 11 − y ˉ M 10 , μ 20 = M 20 − x ˉ M 10 , μ 02 = M 02 − y ˉ M 01 , μ 21 = M 21 − 2 x ˉ M 11 − y ˉ M 20 + 2 x ˉ 2 M 01 , μ 12 = M 12 − 2 y ˉ M 11 − x ˉ M 02 + 2 y ˉ 2 M 10 , μ 30 = M 30 − 3 x ˉ M 20 + 2 x ˉ 2 M 10 , μ 03 = M 03 − 3 y ˉ M 02 + 2 y ˉ 2 M 01 . \begin{aligned} &\mu_{00}=M_{00}, \\ &\mu_{01}=0, \\ &\mu_{10}=0, \\ &\mu_{11}=M_{11}-\bar{x} M_{01}=M_{11}-\bar{y} M_{10}, \\ &\mu_{20}=M_{20}-\bar{x} M_{10}, \\ &\mu_{02}=M_{02}-\bar{y} M_{01}, \\ &\mu_{21}=M_{21}-2 \bar{x} M_{11}-\bar{y} M_{20}+2 \bar{x}^{2} M_{01}, \\ &\mu_{12}=M_{12}-2 \bar{y} M_{11}-\bar{x} M_{02}+2 \bar{y}^{2} M_{10}, \\ &\mu_{30}=M_{30}-3 \bar{x} M_{20}+2 \bar{x}^{2} M_{10}, \\ &\mu_{03}=M_{03}-3 \bar{y} M_{02}+2 \bar{y}^{2} M_{01} . \end{aligned} μ00=M00,μ01=0,μ10=0,μ11=M11−xˉM01=M11−yˉM10,μ20=M20−xˉM10,μ02=M02−yˉM01,μ21=M21−2xˉM11−yˉM20+2xˉ2M01,μ12=M12−2yˉM11−xˉM02+2yˉ2M10,μ30=M30−3xˉM20+2xˉ2M10,μ03=M03−3yˉM02+2yˉ2M01.
可以写成:
μ p q = ∑ m p ∑ n q ( p m ) ( q n ) ( − x ˉ ) ( p − m ) ( − y ˉ ) ( q − n ) M m n \mu_{p q}=\sum_{m}^{p} \sum_{n}^{q}\left(\begin{array}{c} p \\ m \end{array}\right)\left(\begin{array}{c} q \\ n \end{array}\right)(-\bar{x})^{(p-m)}(-\bar{y})^{(q-n)} M_{m n} μpq=m∑pn∑q(pm)(qn)(−xˉ)(p−m)(−yˉ)(q−n)Mmn
中心矩是平移不变的.
Constructing Covariance Matrix Using Second-Order Central Moments,The orientation information of the image can be obtained.
μ 20 ′ = μ 20 / μ 00 = M 20 / M 00 − x ˉ 2 μ 02 ′ = μ 02 / μ 00 = M 02 / M 00 − y ˉ 2 μ 11 ′ = μ 11 / μ 00 = M 11 / M 00 − x ˉ y ˉ \begin{aligned} &\mu_{20}^{\prime}=\mu_{20} / \mu_{00}=M_{20} / M_{00}-\bar{x}^{2} \\ &\mu_{02}^{\prime}=\mu_{02} / \mu_{00}=M_{02} / M_{00}-\bar{y}^{2} \\ &\mu_{11}^{\prime}=\mu_{11} / \mu_{00}=M_{11} / M_{00}-\bar{x} \bar{y} \end{aligned} μ20′=μ20/μ00=M20/M00−xˉ2μ02′=μ02/μ00=M02/M00−yˉ2μ11′=μ11/μ00=M11/M00−xˉyˉ
图像 I ( x , y ) I(x, y) I(x,y)The covariance matrix becomes:
cov [ I ( x , y ) ] = [ μ 20 ′ μ 11 ′ μ 11 ′ μ 02 ′ ] \operatorname{cov}[I(x, y)]=\left[\begin{array}{ll} \mu_{20}^{\prime} & \mu_{11}^{\prime} \\ \mu_{11}^{\prime} & \mu_{02}^{\prime} \end{array}\right] cov[I(x,y)]=[μ20′μ11′μ11′μ02′]
The eigenvalues of the covariance matrix are:
λ i = μ 20 ′ + μ 02 ′ 2 ± 4 μ 11 ′ 2 + ( μ 20 ′ − μ 02 ′ ) 2 2 \lambda_{i}=\frac{\mu_{20}^{\prime}+\mu_{02}^{\prime}}{2} \pm \frac{\sqrt{4 \mu_{11}^{\prime 2}+\left(\mu_{20}^{\prime}-\mu_{02}^{\prime}\right)^{2}}}{2} λi=2μ20′+μ02′±24μ11′2+(μ20′−μ02′)2
It is proportional to the square of the length of the eigenvector axis.因此,Relative differences in the magnitude of the eigenvalues can indicate the eccentricity of the image,or the degree to which it is stretched.The formula for calculating the eccentricity is:
1 − λ 2 λ 1 \sqrt{1-\frac{\lambda_{2}}{\lambda_{1}}} 1−λ1λ2
- centroid_local
@property
def centroid_local(self):
M = self.moments
M0 = M[(0,) * self._ndim]
def _get_element(axis):
return (0,) * axis + (1,) + (0,) * (self._ndim - 1 - axis)
return np.asarray(
tuple(M[_get_element(axis)] / M0 for axis in range(self._ndim)))
扩展 (矩)
参考: https://en.wikipedia.org/wiki/Image_moment
原始矩
对于二维连续函数f(x,y),(p + q)阶矩(Primitive Moment)定义为:
M p q = ∫ − ∞ ∞ ∫ − ∞ ∞ x p y q f ( x , y ) d x d y M_{p q}=\int_{-\infty}^{\infty} \int_{-\infty}^{\infty} x^{p} y^{q} f(x, y) d x d y Mpq=∫−∞∞∫−∞∞xpyqf(x,y)dxdy
对于p,q = 0,1,2,…Adapt it to pixel intensities asI(x,y)的标量(灰度)图像,original image momentMij计算为:
M i j = ∑ x ∑ y x i y j I ( x , y ) M_{i j}=\sum_{x} \sum_{y} x^{i} y^{j} I(x, y) Mij=x∑y∑xiyjI(x,y)
在某些情况下,This can be calculated by considering the image as a probability density function,即,by dividing by the above
∑ x ∑ y I ( x , y ) \sum_{x} \sum_{y} I(x, y) x∑y∑I(x,y)
a uniqueness theorem(Hu[1962])指出,如果f(x,y)是分段连续的,且仅在xyhas non-zero values on finite parts of the plane,then all order moments exist,and sequence of moments(Mpq)是由f(x,y)唯一确定的.相反,(Mpq)唯一确定f(x,y).在实际应用中,The image is summed up in a few low order moment function.
Simple image properties computable by raw moments are:
面积 (for binary images)or grayscale sum(for grayscale images): M 00 M_{00} M00
中心: { x ˉ , y ˉ } = { M 10 M 00 , M 01 M 00 } \{\bar{x}, \bar{y}\}=\left\{\frac{M_{10}}{M_{00}}, \frac{M_{01}}{M_{00}}\right\} { xˉ,yˉ}={ M00M10,M00M01}
中心矩
The central moment is defined as:
μ p q = ∫ − ∞ ∞ ∫ − ∞ ∞ ( x − x ˉ ) p ( y − y ˉ ) q f ( x , y ) d x d y \mu_{p q}=\int_{-\infty}^{\infty} \int_{-\infty}^{\infty}(x-\bar{x})^{p}(y-\bar{y})^{q} f(x, y) d x d y μpq=∫−∞∞∫−∞∞(x−xˉ)p(y−yˉ)qf(x,y)dxdy
其中, x ˉ = M 10 M 00 \bar{x}=\frac{M_{10}}{M_{00}} xˉ=M00M10, y ˉ = M 01 M 00 \bar{y}=\frac{M_{01}}{M_{00}} yˉ=M00M01,is the mass of the centroid
如果 f ( x , y ) f(x, y) f(x,y)is a digital image,上面的公式变为:
μ p q = ∑ x ∑ y ( x − x ˉ ) p ( y − y ˉ ) q f ( x , y ) \mu_{p q}=\sum_{x} \sum_{y}(x-\bar{x})^{p}(y-\bar{y})^{q} f(x, y) μpq=x∑y∑(x−xˉ)p(y−yˉ)qf(x,y)
The third order central moment is:
μ 00 = M 00 , μ 01 = 0 , μ 10 = 0 , μ 11 = M 11 − x ˉ M 01 = M 11 − y ˉ M 10 , μ 20 = M 20 − x ˉ M 10 , μ 02 = M 02 − y ˉ M 01 , μ 21 = M 21 − 2 x ˉ M 11 − y ˉ M 20 + 2 x ˉ 2 M 01 , μ 12 = M 12 − 2 y ˉ M 11 − x ˉ M 02 + 2 y ˉ 2 M 10 , μ 30 = M 30 − 3 x ˉ M 20 + 2 x ˉ 2 M 10 , μ 03 = M 03 − 3 y ˉ M 02 + 2 y ˉ 2 M 01 . \begin{aligned} &\mu_{00}=M_{00}, \\ &\mu_{01}=0, \\ &\mu_{10}=0, \\ &\mu_{11}=M_{11}-\bar{x} M_{01}=M_{11}-\bar{y} M_{10}, \\ &\mu_{20}=M_{20}-\bar{x} M_{10}, \\ &\mu_{02}=M_{02}-\bar{y} M_{01}, \\ &\mu_{21}=M_{21}-2 \bar{x} M_{11}-\bar{y} M_{20}+2 \bar{x}^{2} M_{01}, \\ &\mu_{12}=M_{12}-2 \bar{y} M_{11}-\bar{x} M_{02}+2 \bar{y}^{2} M_{10}, \\ &\mu_{30}=M_{30}-3 \bar{x} M_{20}+2 \bar{x}^{2} M_{10}, \\ &\mu_{03}=M_{03}-3 \bar{y} M_{02}+2 \bar{y}^{2} M_{01} . \end{aligned} μ00=M00,μ01=0,μ10=0,μ11=M11−xˉM01=M11−yˉM10,μ20=M20−xˉM10,μ02=M02−yˉM01,μ21=M21−2xˉM11−yˉM20+2xˉ2M01,μ12=M12−2yˉM11−xˉM02+2yˉ2M10,μ30=M30−3xˉM20+2xˉ2M10,μ03=M03−3yˉM02+2yˉ2M01.
可以写成:
μ p q = ∑ m p ∑ n q ( p m ) ( q n ) ( − x ˉ ) ( p − m ) ( − y ˉ ) ( q − n ) M m n \mu_{p q}=\sum_{m}^{p} \sum_{n}^{q}\left(\begin{array}{c} p \\ m \end{array}\right)\left(\begin{array}{c} q \\ n \end{array}\right)(-\bar{x})^{(p-m)}(-\bar{y})^{(q-n)} M_{m n} μpq=m∑pn∑q(pm)(qn)(−xˉ)(p−m)(−yˉ)(q−n)Mmn
中心矩是平移不变的.
Constructing Covariance Matrix Using Second-Order Central Moments,The orientation information of the image can be obtained.
μ 20 ′ = μ 20 / μ 00 = M 20 / M 00 − x ˉ 2 μ 02 ′ = μ 02 / μ 00 = M 02 / M 00 − y ˉ 2 μ 11 ′ = μ 11 / μ 00 = M 11 / M 00 − x ˉ y ˉ \begin{aligned} &\mu_{20}^{\prime}=\mu_{20} / \mu_{00}=M_{20} / M_{00}-\bar{x}^{2} \\ &\mu_{02}^{\prime}=\mu_{02} / \mu_{00}=M_{02} / M_{00}-\bar{y}^{2} \\ &\mu_{11}^{\prime}=\mu_{11} / \mu_{00}=M_{11} / M_{00}-\bar{x} \bar{y} \end{aligned} μ20′=μ20/μ00=M20/M00−xˉ2μ02′=μ02/μ00=M02/M00−yˉ2μ11′=μ11/μ00=M11/M00−xˉyˉ
图像 I ( x , y ) I(x, y) I(x,y)The covariance matrix becomes:
cov [ I ( x , y ) ] = [ μ 20 ′ μ 11 ′ μ 11 ′ μ 02 ′ ] \operatorname{cov}[I(x, y)]=\left[\begin{array}{ll} \mu_{20}^{\prime} & \mu_{11}^{\prime} \\ \mu_{11}^{\prime} & \mu_{02}^{\prime} \end{array}\right] cov[I(x,y)]=[μ20′μ11′μ11′μ02′]
The eigenvalues of the covariance matrix are:
λ i = μ 20 ′ + μ 02 ′ 2 ± 4 μ 11 ′ 2 + ( μ 20 ′ − μ 02 ′ ) 2 2 \lambda_{i}=\frac{\mu_{20}^{\prime}+\mu_{02}^{\prime}}{2} \pm \frac{\sqrt{4 \mu_{11}^{\prime 2}+\left(\mu_{20}^{\prime}-\mu_{02}^{\prime}\right)^{2}}}{2} λi=2μ20′+μ02′±24μ11′2+(μ20′−μ02′)2
It is proportional to the square of the length of the eigenvector axis.因此,Relative differences in the magnitude of the eigenvalues can indicate the eccentricity of the image,or the degree to which it is stretched.The formula for calculating the eccentricity is:
1 − λ 2 λ 1 \sqrt{1-\frac{\lambda_{2}}{\lambda_{1}}} 1−λ1λ2
不变矩
Moments are known for their applications in image analysis,as they can be used to obtain invariants about a specific transformation class.
在这种情况下,术语 Moment invariants often appear.然而,When the invariant consists of moments,The only thing that is itself invariant is the central moment.
注意,The invariants detailed below are completely invariant only in the continuous domain.在离散域中,Neither scaling nor rotation is well defined:Discrete images transformed in this way are usually an approximation,and the transformation is irreversible.因此,When describing shapes in discrete images,These invariants are just近似不变的.
平移不变
Central moments of all orders μ i j μ_{ij} μij,通过构造,invariant to translation.
缩放不变
Translation and scale invariants η i j η_{ij} ηijcan be composed of central moments,By dividing by the appropriate scale of the zero point central moment:
η i j = μ i j μ 00 ( 1 + i + j 2 ) \eta_{i j}=\frac{\mu_{i j}}{\mu_{00}^{\left(1+\frac{i+j}{2}\right)}} ηij=μ00(1+2i+j)μij
其中, i + j ≥ 2 i+j \geq 2 i+j≥2.注意,Trial translation invariant only when using the central moment.
旋转不变
如Hu[1][2]的工作所示,can be constructed about translation、Scale and rotation invariants:
I 1 = η 20 + η 02 I 2 = ( η 20 − η 02 ) 2 + 4 η 11 2 I 3 = ( η 30 − 3 η 12 ) 2 + ( 3 η 21 − η 03 ) 2 I 4 = ( η 30 + η 12 ) 2 + ( η 21 + η 03 ) 2 I 5 = ( η 30 − 3 η 12 ) ( η 30 + η 12 ) [ ( η 30 + η 12 ) 2 − 3 ( η 21 + η 03 ) 2 ] + ( 3 η 21 − η 03 ) ( η 21 + η 03 ) [ 3 ( η 30 + η 12 ) 2 − ( η 21 + η 03 ) 2 ] I 6 = ( η 20 − η 02 ) [ ( η 30 + η 12 ) 2 − ( η 21 + η 03 ) 2 ] + 4 η 11 ( η 30 + η 12 ) ( η 21 + η 03 ) I 7 = ( 3 η 21 − η 03 ) ( η 30 + η 12 ) [ ( η 30 + η 12 ) 2 − 3 ( η 21 + η 03 ) 2 ] − ( η 30 − 3 η 12 ) ( η 21 + η 03 ) [ 3 ( η 30 + η 12 ) 2 − ( η 21 + η 03 ) 2 ] \begin{aligned} &I_{1}=\eta_{20}+\eta_{02} \\ &I_{2}=\left(\eta_{20}-\eta_{02}\right)^{2}+4 \eta_{11}^{2} \\ &I_{3}=\left(\eta_{30}-3 \eta_{12}\right)^{2}+\left(3 \eta_{21}-\eta_{03}\right)^{2} \\ &I_{4}=\left(\eta_{30}+\eta_{12}\right)^{2}+\left(\eta_{21}+\eta_{03}\right)^{2} \\ &I_{5}=\left(\eta_{30}-3 \eta_{12}\right)\left(\eta_{30}+\eta_{12}\right)\left[\left(\eta_{30}+\eta_{12}\right)^{2}-3\left(\eta_{21}+\eta_{03}\right)^{2}\right]+\left(3 \eta_{21}-\eta_{03}\right)\left(\eta_{21}+\eta_{03}\right)\left[3\left(\eta_{30}+\eta_{12}\right)^{2}-\left(\eta_{21}+\eta_{03}\right)^{2}\right] \\ &I_{6}=\left(\eta_{20}-\eta_{02}\right)\left[\left(\eta_{30}+\eta_{12}\right)^{2}-\left(\eta_{21}+\eta_{03}\right)^{2}\right]+4 \eta_{11}\left(\eta_{30}+\eta_{12}\right)\left(\eta_{21}+\eta_{03}\right) \\ &I_{7}=\left(3 \eta_{21}-\eta_{03}\right)\left(\eta_{30}+\eta_{12}\right)\left[\left(\eta_{30}+\eta_{12}\right)^{2}-3\left(\eta_{21}+\eta_{03}\right)^{2}\right]-\left(\eta_{30}-3 \eta_{12}\right)\left(\eta_{21}+\eta_{03}\right)\left[3\left(\eta_{30}+\eta_{12}\right)^{2}-\left(\eta_{21}+\eta_{03}\right)^{2}\right] \end{aligned} I1=η20+η02I2=(η20−η02)2+4η112I3=(η30−3η12)2+(3η21−η03)2I4=(η30+η12)2+(η21+η03)2I5=(η30−3η12)(η30+η12)[(η30+η12)2−3(η21+η03)2]+(3η21−η03)(η21+η03)[3(η30+η12)2−(η21+η03)2]I6=(η20−η02)[(η30+η12)2−(η21+η03)2]+4η11(η30+η12)(η21+η03)I7=(3η21−η03)(η30+η12)[(η30+η12)2−3(η21+η03)2]−(η30−3η12)(η21+η03)[3(η30+η12)2−(η21+η03)2]
these are knownHu矩不变量.
第一个 I 1 I_1 I1,Similar to the surrounding image center of mass moment of inertia,where the intensity of the pixel is similar to the physical density.前六个 I 1 , . . . I 6 I_1,...I_6 I1,...I6反射对称,比如,If the image changes to image,then these parameters remain unchanged.最后一个 I 7 I_7 I7,is reflective antisymmetric(Sign change in case of reflection),This enables it to distinguish mirror images of other identical images.
J. Flusser.[3]Put forward for rotating moment invariants complete independent set of general theory.He proved that traditional hu moment invariant set is not independent of each other,也不是完全的.I3不是很有用,because it depends on other(如何?)在原HuA third-order independent invariant is missing from the set:
I 8 = η 11 [ ( η 30 + η 12 ) 2 − ( η 03 + η 21 ) 2 ] − ( η 20 − η 02 ) ( η 30 + η 12 ) ( η 03 + η 21 ) I_{8}=\eta_{11}\left[\left(\eta_{30}+\eta_{12}\right)^{2}-\left(\eta_{03}+\eta_{21}\right)^{2}\right]-\left(\eta_{20}-\eta_{02}\right)\left(\eta_{30}+\eta_{12}\right)\left(\eta_{03}+\eta_{21}\right) I8=η11[(η30+η12)2−(η03+η21)2]−(η20−η02)(η30+η12)(η03+η21)
和 I 7 I_7 I7一样, I 8 I_8 I8is also reflective antisymmetric.
后来,J. Flusser和T. Suk[4]将nTheoretical Specialization of a Rotationally Symmetric Shape.
应用
Zhang等人应用HuMoment invariants to address pathological brain detection(PBD)问题Doerr和FlorenceUtilize target orientation information related to second-order central moments,从微xEfficient extraction of translation- and rotation-invariant target sections from tomography image data[6].
equivalent_diameter_area
参考:W. Pabst, E. Gregorová. Characterization of particles and particle
systems, pp. 27-28. ICT Prague, 2007.
https://old.vscht.cz/sil/keramika/Characterization_of_particles/CPPS%20_English%20version_.pdf
边栏推荐
- share总结
- unity框架之缓存池
- manipulation of file contents
- Significant differences between Oracle and Postgresql in PLSQL transaction rollback
- Take care of JVM performance optimization (own note version)
- Basic characteristics of TL431 and oscillator circuit
- 嵌入式数据库开发编程MySQL(全)
- 转:管理是对可能性的热爱,管理者要有闯进未知的勇气
- Eight guiding principles to help businesses achieve digital transformation success
- 【技巧】借助Sentinel实现请求的优先处理
猜你喜欢
随机推荐
Introduction and application of go module
自定义通用分页标签01
Simple operation of the file system
【源码】使用深度学习训练一个游戏
2022软件测试面试题 最新字节跳动50道真题面试题 刷完已拿下15k 附讲解+答疑
ADC噪声全面分析 -03- 利用噪声分析进行实际设计
if,case,for,while
7-3 LVS+Keepalived集群叙述与部署
马尔可夫链
2022 Hangzhou Electric Power Multi-School League Game 5 Solution
Hey, I had another fight with HR in the small group!
Introduction to mq application scenarios
拿捏JVM性能优化(自己笔记版本)
7-2 LVS+DR Overview and Deployment
Basic characteristics of TL431 and oscillator circuit
SVM介绍以及实战
2003. 每棵子树内缺失的最小基因值 DFS
学会iframe并用其解决跨域问题
sql语句查询String类型字段小于10的怎么查
Structure function exercise

![The video of machine learning to learn [update]](/img/e7/c9a17b4816ce8d4b0787c451520ac3.png)