leetcode：210. 課程錶 II

題目來源

• leetcode

題目描述

題目解析

只有有向無環圖才有拓撲序

拓撲排序並不是一個純粹的排序算法，它只是針對某一類圖，找到一個可以執行的線性順序。

針對哪類圖呢？有向無環圖。即使：

• 這個圖的邊必須是有方向的；
• 圖內無環。

那麼什麼是方向呢？

比如微信好友就是有向的，你加了他好友他可能把你删了你卻不知道。。。那這個朋友關系就是單向的。。

什麼是環？環是和方向有關的，從一個點出發能回到自己，這是環。

所以下圖左邊不是環，右邊是。

那麼如果一個圖裏有環，比如右圖，想執行1就要先執行3，想執行3就要先執行2，想執行2就要先執行1，這成了個死循環，無法找到正確的打開方式，所以找不到它的一個拓撲序。

結論：

• 如果這個圖不是 DAG，那麼它是沒有拓撲序的；
• 如果是 DAG，那麼它至少有一個拓撲序；
• 反之，如果它存在一個拓撲序，那麼這個圖必定是 DGA。

對於本題，拓撲排序的意思是：求解一種可行的順序，能够讓我把所有課都學了。

那應該怎麼做呢？

（1）首先我們可以用圖來描述它，圖的兩個要素是頂點和邊，那麼在這裏：

• 頂點：每門課
• 邊：起點的課程是終點的課程的先修課

假如有一個這樣的圖：

這種圖叫AOV(Activity On Vertex) 網絡，在這種圖裏：

• 頂點：錶示活動；
• 邊：錶示活動間的先後關系

所以一個 AOV 網應該是一個 DAG，即有向無環圖，否則某些活動會無法進行。

那麼所有活動可以排成一個可行線性序列，這個序列就是拓撲序列。

那麼這個序列的實際意義是：

按照這個順序，在每個項目開始時，能够保證它的前驅活動都已完成，從而使整個工程順利進行。

回到我們這個例子中：

• 我們一眼可以看出來要先學 C1, C2，因為這兩門課沒有任何要求嘛，大一的時候就學唄；
• 大二就可以學第二行的 C3, C5, C8 了，因為這三門課的先修課程就是 C1, C2，我們都學完了；
• 大三可以學第三行的 C4, C9；
• 最後一年選剩下的 C6, C7。

這樣，我們就把所有課程學完了，也就得到了這個圖的一個拓撲排序。

注意，有時候拓撲序並不是唯一的，比如在這個例子中，先學 C1 再學 C2，和先 C2 後 C1 都行，都是這個圖的正確的拓撲序，但這是兩個順序了。

所以面試的時候要問下面試官，是要求解任意解，還是列出所有解。

在這個圖裏的邊錶示的是一種依賴關系，如果要修下一門課，就要先把前一門課修了

這和打遊戲裏一樣一樣的嘛，要拿到一個道具，就要先做 A 任務，再完成 B 任務，最終終於能到達目的地了。

在上面的圖裏，大家很容易就看出來了它的拓撲序，但當工程越來越龐大時，依賴關系也會變得錯綜複雜，那就需要用一種系統性的方式方法來求解了。

那麼我們回想一下剛剛自己找拓撲序的過程，為什麼我們先看上了 C1, C2?

因為它們沒有依賴別人啊，也就是它的入度為 0.

• 入度：頂點的入度是指「指向該頂點的邊」的數量；
• 出度：頂點的出度是指該頂點指向其他點的邊的數量。

所以我們先執行入度為 0 的那些點，因此我們要先記錄每個頂點的入度。因為只有當它的入度為 0的時候，我們才能執行它。

在剛才的例子裏，最開始 C1, C2 的入度就是 0，所以我們可以先執行這兩個。

那在這個算法裏第一步就是得到每個頂點的入度。

（1）預處理得到每個點的入度

我們可以用一個 HashMap 來存放這個信息，或者用一個數組會更精巧。

拿到了這個之後，就可以執行入度為 0 的這些點了，也就是 C1, C2.

那我們把可以被執行的這些點，放入一個待執行的容器裏，這樣之後我們一個個的從這個容器裏取頂點就好了。

至於這個容器究竟選哪種數據結構，這取决於我們需要做哪些操作，再看哪種數據結構可以為之服務。

那麼首先可以把**[C1, C2]**放入容器中，

然後想想我們需要哪些操作吧！

我們最常做的操作無非就是把點放進來，把點拿出去執行了，所以可以用一個queue

其他的也行，放進來這個容器裏的頂點的地比特都是一樣的，都是可以執行的，和進來的順序無關，但何必非得給自己找麻煩呢？一個常規順序的簡簡單單的 queue 就够用了。

然後就需要把某些點拿出去執行了。

當我們把 C1 拿出來執行，那這意味這什麼？

答：意味著「以 C1 為頂點」的「指向其他點」的「邊」都消失了，也就是 C1 的出度變成了 0.

如下圖，也就是這兩條邊可以消失了。

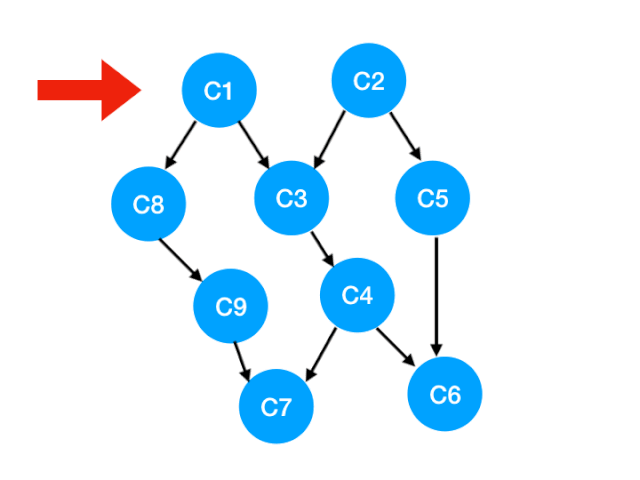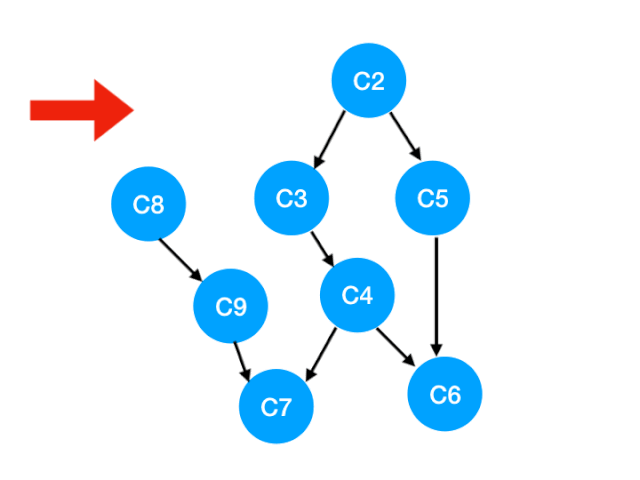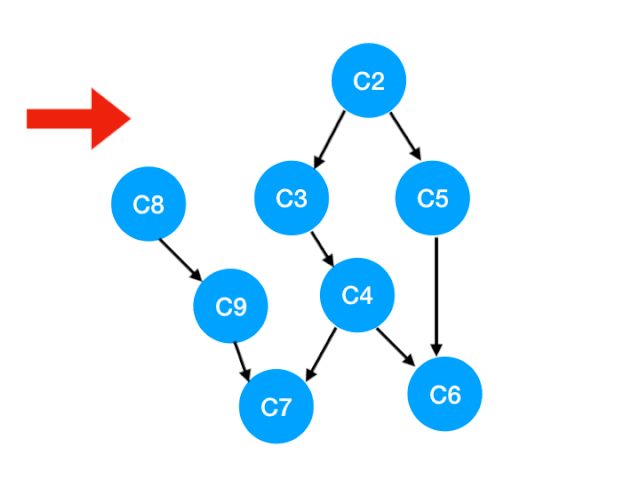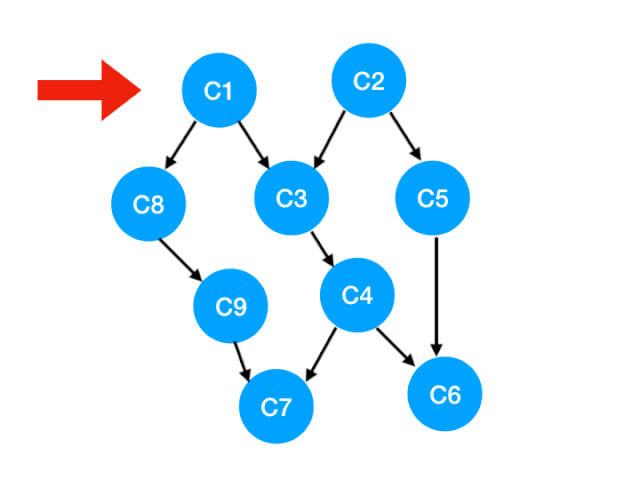
那麼此時我們就可以更新 C1 所指向的那些點也就是 C3 和 C8 的 入度 了，更新後的數組如下：

那我們這裏看到很關鍵的一步，C8 的入度變成了 0！

也就意味著 C8 此時沒有了任何依賴，可以放到我們的 queue 裏等待執行了。

此時我們的 queue 裏就是：[C2, C8].

下一個我們再執行 C2

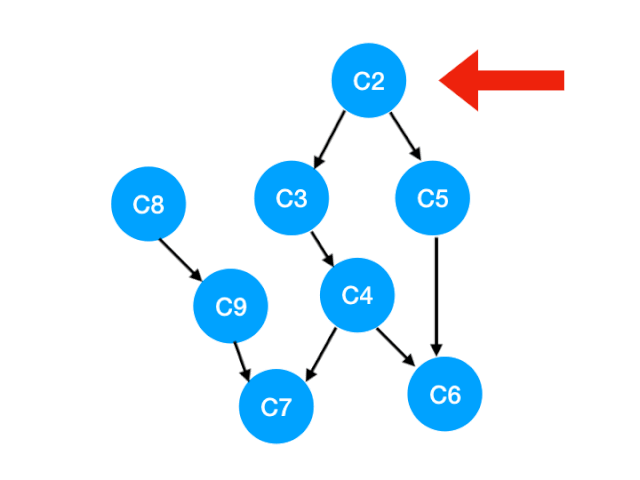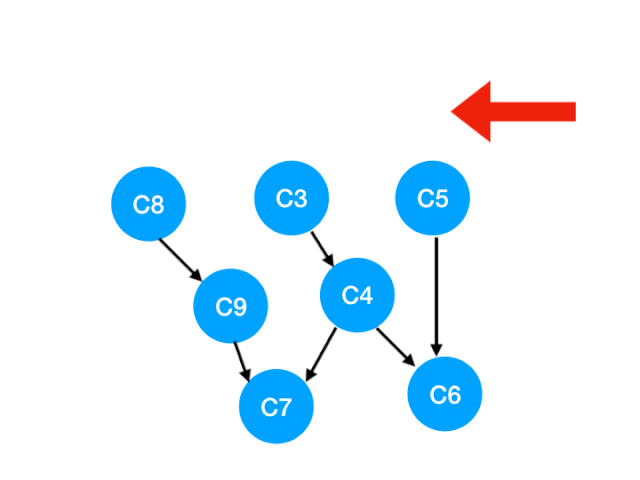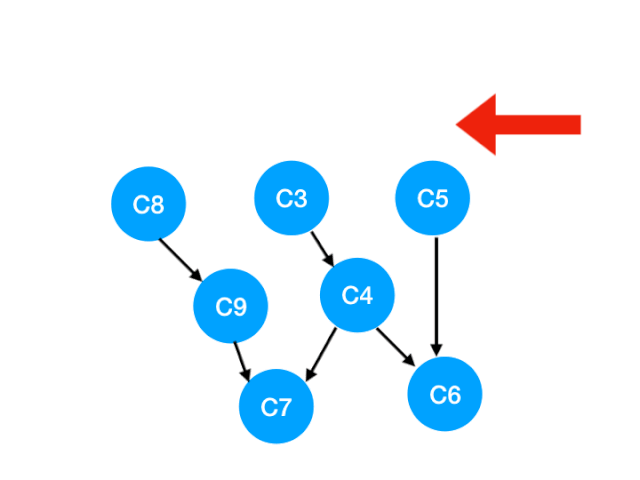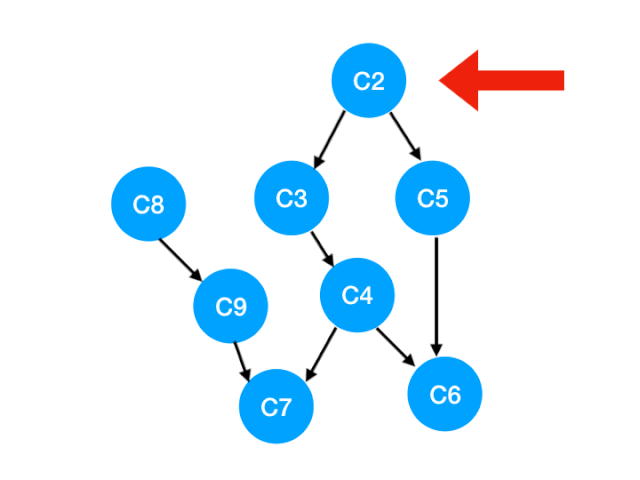
那麼 C2 所指向的 C3, C5 的 入度-1，

更新錶格：

也就是 C3 和 C5 都沒有了任何束縛，可以放進 queue 裏執行了。

queue 此時變成：[C8, C3, C5]
那麼下一步我們執行 C8

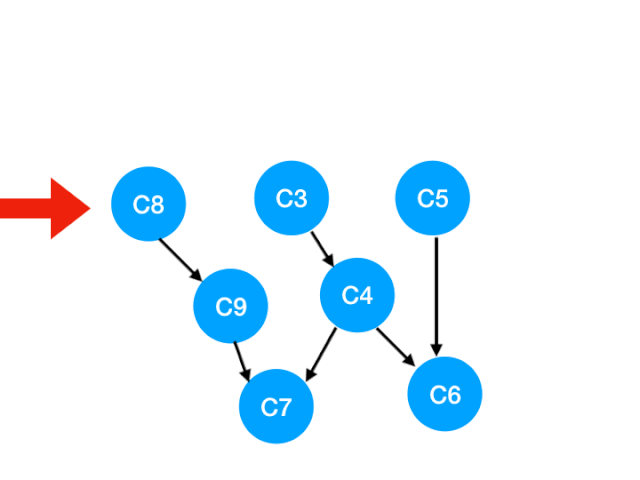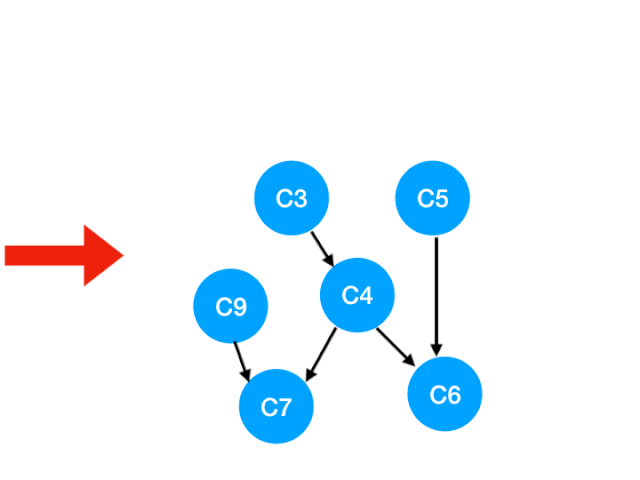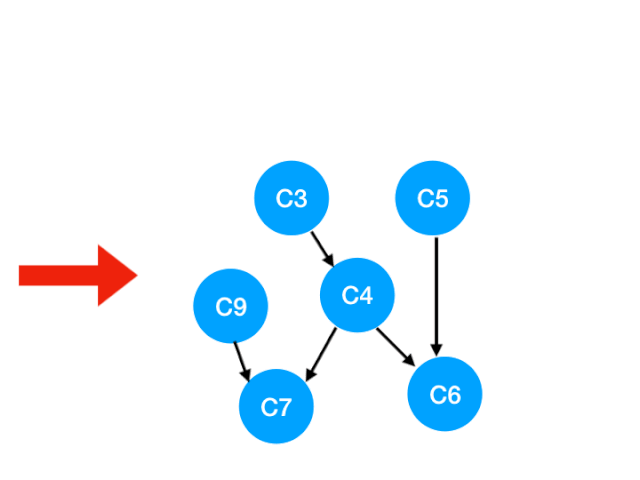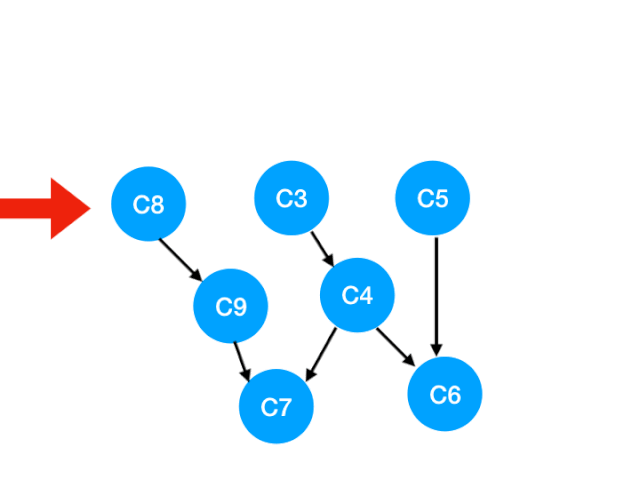
相應的 C8 所指的 C9 的入度-1.更新錶格：

那麼 C9 沒有了任何要求，可以放進 queue 裏執行了。

queue 此時變成：[C3, C5, C9]

接下來執行 C3，

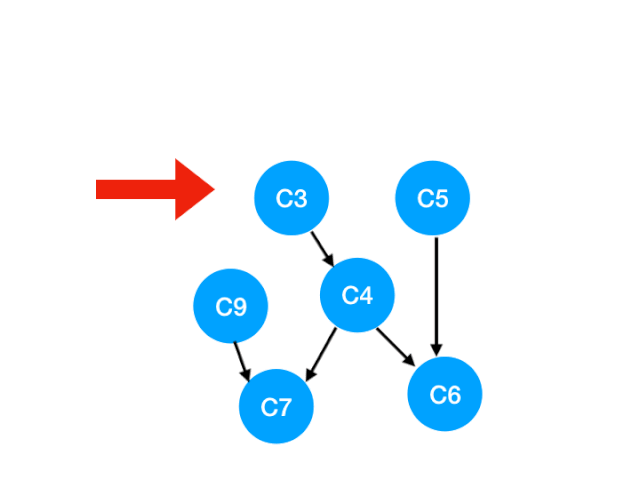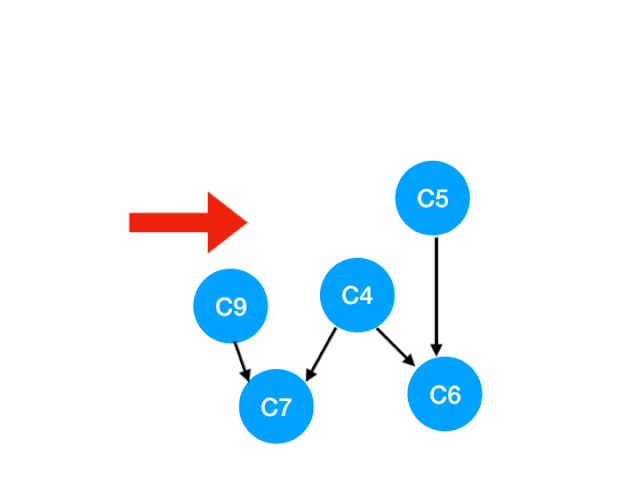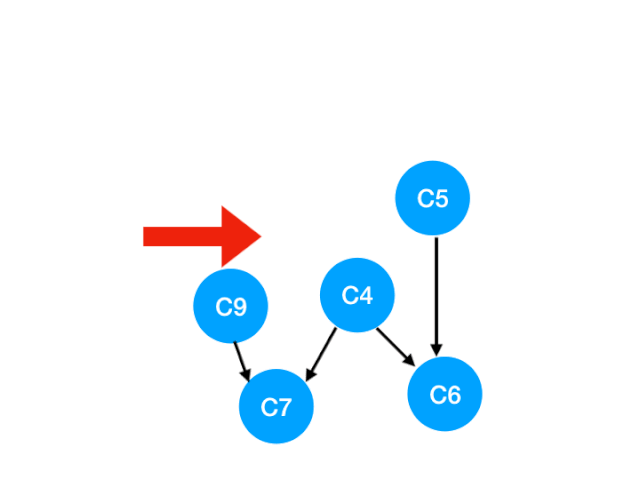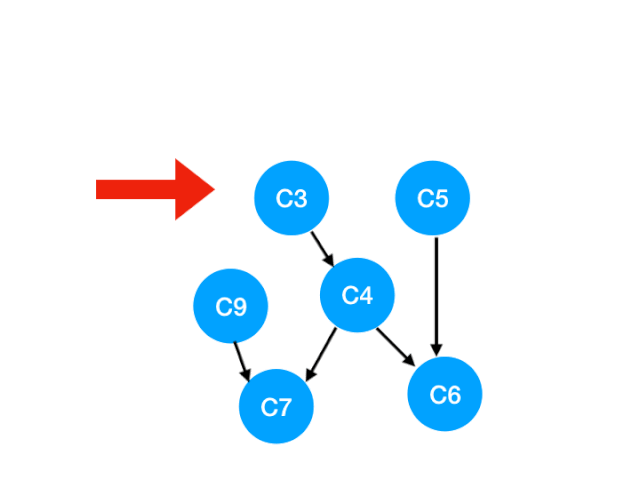
相應的 C3 所指的 C4 的入度-1.更新錶格：

但是 C4 的入度並沒有變成 0，所以這一步沒有任何點可以加入 queue。

queue 此時變成 [C5, C9]

再執行 C5

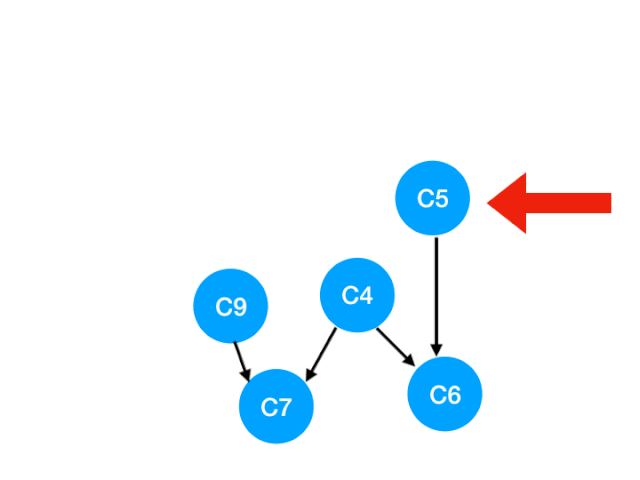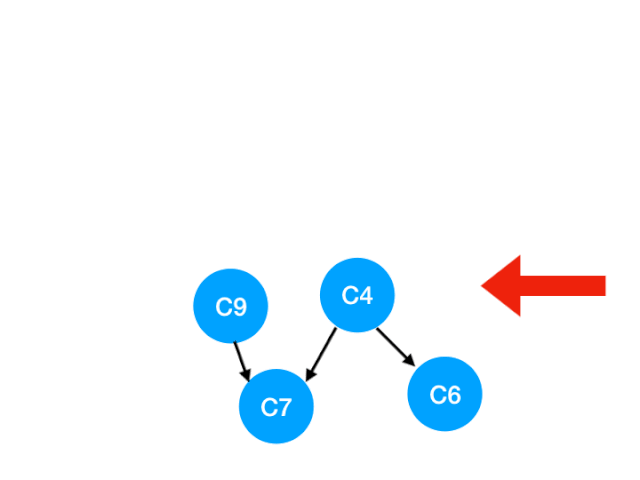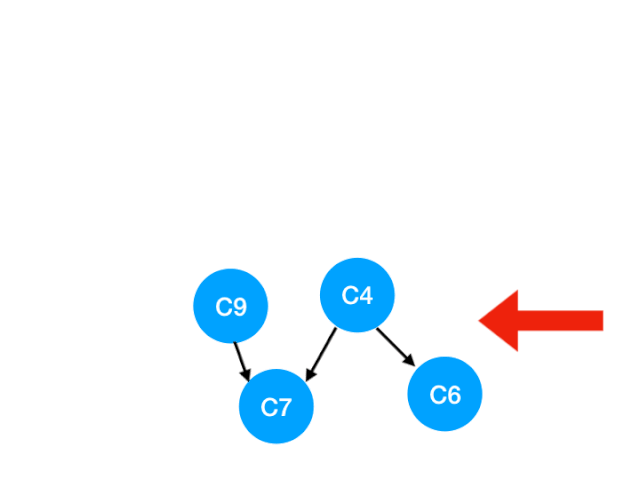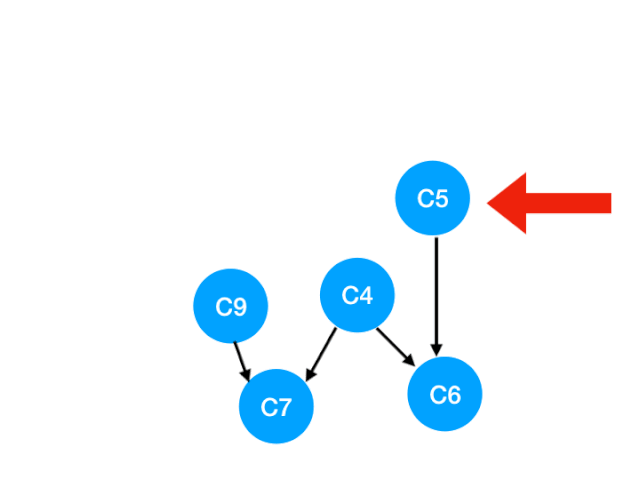
那麼 C5 所指的 C4 和 C6 的入度- 1.更新錶格：

這裏 C4 的依賴全都消失啦，那麼可以把 C4 放進 queue 裏了：

queue = [C9, C4]

Step6

然後執行 C9

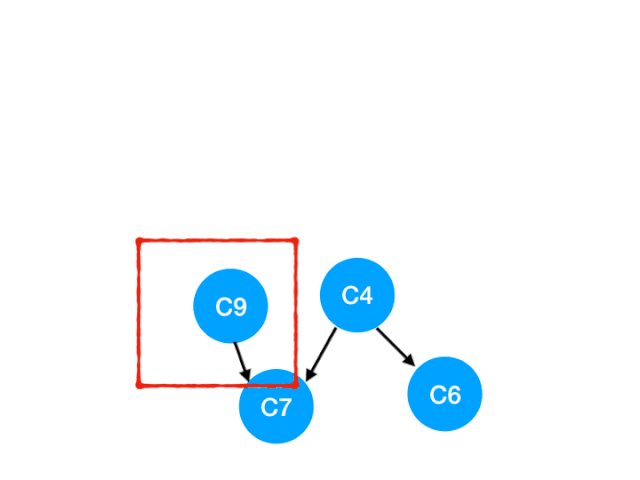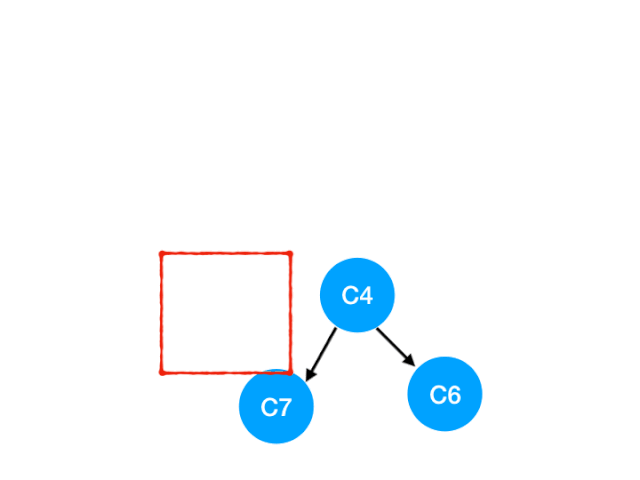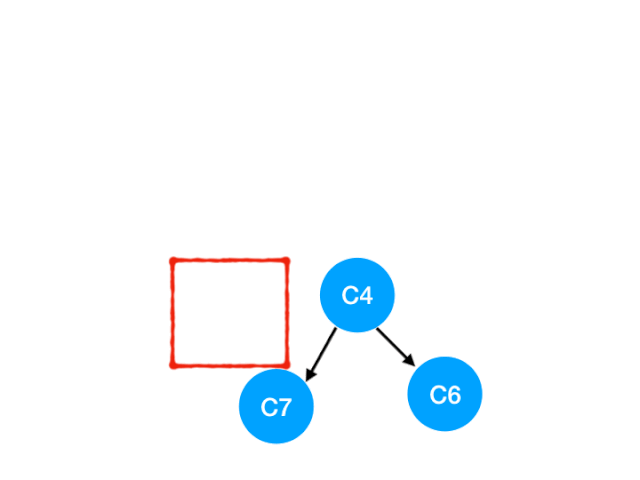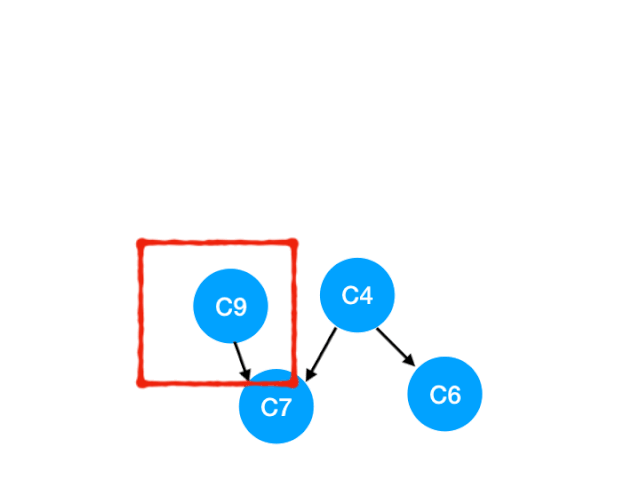
那麼 C9 所指的 C7 的入度- 1

這裏 C7 的入度並不為 0，還不能加入 queue，

此時 queue = [C4]
接著執行 C4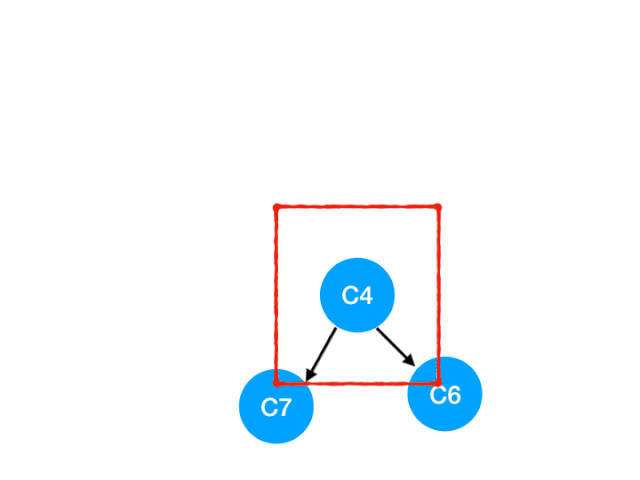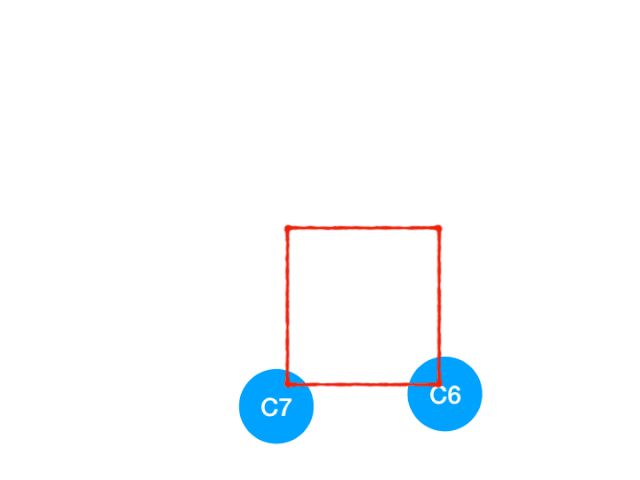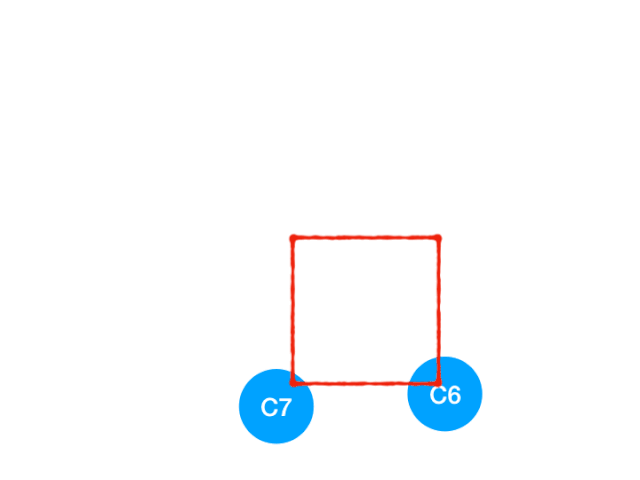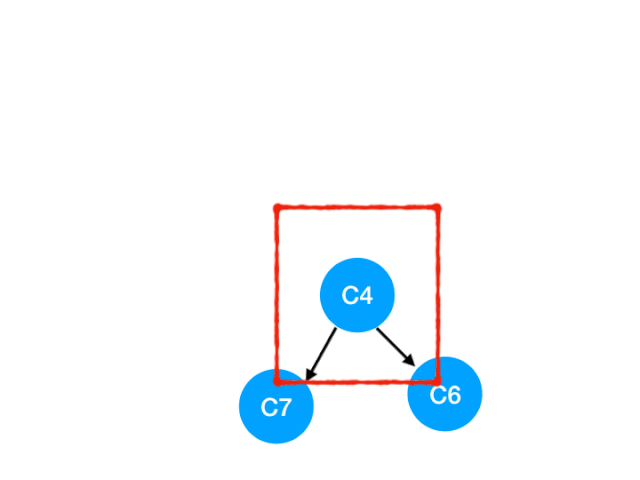

所以 C4 所指向的 C6 和 C7 的入度-1，更新錶格：

C6 和 C7 的入度都變成 0 啦！！把它們放入 queue，繼續執行到直到 queue 為空即可

時間複雜度

空間複雜度