当前位置:网站首页>逆序对对数计算,顺序对对数计算——归并排序
逆序对对数计算,顺序对对数计算——归并排序
2022-06-29 02:46:00 【疯疯癫癫才自由】
/如果第二个序列的这个数(没比较的第一个数,
//因为序列是已经有序了,这个数必定是第二段序列还没比较的数中最小的数,)
//比第一个序列的还没比较的任何数小,则第一段序列的还没比较的数都能和
//第二段序列的这个数构成逆序对
void my_merge(int *a,int l1,int r1,int l2,int r2)//两个有序序列,合并为一个有序序列
{
int temp[r2-l1+1],index=0,i=l1,j=l2;
while(i<=r1&&j<=r2)
{
if(a[i]<=a[j])
temp[index++]=a[i++];
else
{
temp[index++]=a[j++];
res+=r1-i+1; //如果第二个序列的这个数(没比较的第一个数,
//因为序列是已经有序了,这个数必定是第二段序列还没比较的数中最小的数,)
//比第一个序列的还没比较的任何数小,则第一段序列的还没比较的数都能和
//第二段序列的这个数构成逆序对
}
}while(i<=r1)
temp[index++]=a[i++];
while(j<=r2)
temp[index++]=a[j++];
for(i=0;i<index;++i)
a[l1+i]=temp[i];
}
完整代码:
/**
用归并排序求逆序对数
*/
/**
归并排序
tow point :将两个有序序列合并为一个有序序列,O(n)
*/
#include <iostream>
#include <algorithm>
#include <cmath>
#include <cstdlib>
using namespace std;
int res=0;
void my_merge(int *a,int l1,int r1,int l2,int r2)//两个有序序列,合并为一个有序序列
{
int temp[r2-l1+1],index=0,i=l1,j=l2;
while(i<=r1&&j<=r2)
{
if(a[i]<=a[j])
temp[index++]=a[i++];
else
{
temp[index++]=a[j++];
res+=r1-i+1;
}
}
while(i<=r1)
temp[index++]=a[i++];
while(j<=r2)
temp[index++]=a[j++];
for(i=0;i<index;++i)
a[l1+i]=temp[i];
}
void mergesort(int *a,int l,int r)
{
if(l>=r)
return;
else
{
int mid=l+(r-l)/2;
mergesort(a,l,mid);
mergesort(a,mid+1,r);
my_merge(a,l,mid,mid+1,r);
}
}
int main()
{
int n;
cin >> n;
int a[n];
for(int i=0;i<n;++i)
cin >> a[i];
int sum=0;
for(int i=0;i<n;++i)
for(int j=i+1;j<n;++j)
if(a[i]>a[j])//枚举算法
++sum;
printf("sum: %d\n",sum );
mergesort(a,0,n);
for(auto b: a)
cout << b << ' ';
cout << endl;
printf("%d\n",res);
cout << "Hello world!" << endl;
return 0;
}既然逆序对都算出来了,那么顺序对可谓是换汤不换药,顺序对定义:dp[i] < dp[j] (i<j);
下面给出一个题目:用逆序对,顺序对各计算一次:
Description
给定一个数串,数串的长度为 nnn ,现在将一个子串的每个数字之和定义为该子串的数串和,请你求出数串中有多少个子串的数串和为正数。
Input
第一行一个数 nnn ,表示数串的长度。第二行一共 nnn 个数,表示数串中的每个数输出就一个数,表示数串中有多少个子串的数串和为正数。
Output
一个正数即答案。
Sample Input 1
3
8 -9 2Sample Output 1
3Hint
100% nnn ≤ 100000所有数之和在int范围之内
分析: 逆序对求数串问题,求出数列的后缀和,要想得到子串的和为正数,即
dp[i]>dp[j](i<j),即求一个序列中逆序对的对数
/**
逆序对求数串问题,求出数列的后缀和,要想得到子串的和为正数,即
dp[i]>dp[j](i<j),即求一个序列中逆序对的对数
*/
/**
#include <iostream>
using namespace std;
long long res=0; //这儿的res是需要定义为long long,否则会出现答案错误
void my_merge(int *a,int l1,int r1,int l2,int r2)//两个有序序列,合并为一个有序序列
{
int temp[r2-l1+1],index=0,i=l1,j=l2;
while(i<=r1&&j<=r2)
{
if(a[i]<=a[j])
temp[index++]=a[i++];
else
{
temp[index++]=a[j++];
res+=r1-i+1; //如果第二个序列的这个数(没比较的第一个数,
//因为序列是已经有序了,这个数必定是第二段序列还没比较的数中最小的数,)
//比第一个序列的还没比较的任何数小,则第一段序列的还没比较的数都能和
//第二段序列的这个数构成逆序对
}
}
while(i<=r1)
temp[index++]=a[i++];
while(j<=r2)
temp[index++]=a[j++];
for(i=0;i<index;++i)
a[l1+i]=temp[i];
}
void mergesort(int *a,int l,int r)
{
if(l>=r)
return;
else
{
int mid=l+(r-l)/2;
mergesort(a,l,mid);
mergesort(a,mid+1,r);
my_merge(a,l,mid,mid+1,r);
}
}
int main()
{
int n;
scanf("%d",&n);
int a[n+1],dp[n+2],val;
dp[n+1]=0;
for(int i=1;i<=n;++i)
{
scanf("%d",&a[i]);
}
for(int i=n;i>0;--i)
dp[i]=dp[i+1]+a[i]; //dp表示后缀和
mergesort(dp,1,n+1);//这儿的参数是n+1,因为dp[n]-dp[n+1]就表示a[i]这个数的值,
//但是你传递的参数为n的话,最后一个数就被去掉了
printf("%lld\n",res);
return 0;
}
*/ 那么我们是否可以用前缀和来算呢?
前缀和计算即dp[i] < dp[j] (i<j),即求一个序列中顺序对的个数,
同样用递归排序来求
/**
那么我们是否可以用前缀和来算呢?
前缀和计算即dp[i] < dp[j] (i<j),即求一个序列中顺序对的个数,
同样用递归排序来求
*/
#include <iostream>
using namespace std;
long long res=0; //这儿的res是需要定义为long long,否则会出现答案错误
void my_merge(int *a,int l1,int r1,int l2,int r2)//两个有序序列,合并为一个有序序列
{
int temp[r2-l1+1],index=0,i=l1,j=l2;
while(i<=r1&&j<=r2)
{
if(a[i]<a[j])
{
temp[index++]=a[i++];
res+=r2-j+1; //如果第一个序列的这个数(没比较的第一个数,
//因为序列是已经有序了,这个数必定是第一段序列还没比较的数中最小的数,)
//比第二个序列的还没比较的任何数小,则第二段序列的还没比较的数都能和
} //第一段序列的这个数构成顺序对
else
temp[index++]=a[j++];
}
while(i<=r1)
temp[index++]=a[i++];
while(j<=r2)
temp[index++]=a[j++];
for(i=0;i<index;++i)
a[l1+i]=temp[i];
}
void mergesort(int *a,int l,int r)
{
if(l>=r)
return;
else
{
int mid=l+(r-l)/2;
mergesort(a,l,mid);
mergesort(a,mid+1,r);
my_merge(a,l,mid,mid+1,r);
}
}
int main()
{
int n;
scanf("%d",&n);
int dp[n+1],val;
dp[0]=0;
for(int i=1;i<=n;++i)
{
scanf("%d",&val);
dp[i]=dp[i-1]+val; //dp表示数列的前缀和
}
mergesort(dp,0,n);/**这儿的第二个参数是0,因为dp[1]-dp[0]就表示a[1]这个数的值,
但是你传递的参数为1的话,第一个数就被去掉了*/
printf("%lld\n",res);
return 0;
}
边栏推荐
- 短视频平台常见SQL面试题,你学会了吗?
- [untitled]
- Google Maps API v3~ simply turn off infoindow- Google Map API v3 ~ Simply Close an infowindow?
- Relations EMC, EMI, EMS
- String segment combination
- Informatics Olympiad 1361: Produce
- PHP的exec函数
- On the fact that lambda expressions cannot handle recursion
- 18. `bs对象.节点名.next_sibling` 获取兄弟节点
- 1110: nearest common ancestor (function topic)
猜你喜欢

【一起上水硕系列】Day 6-强肝学术论文!最细解释!

Altium Designer中从已有的PCB中导出所有元件的封装的方法

Download and installation of MySQL
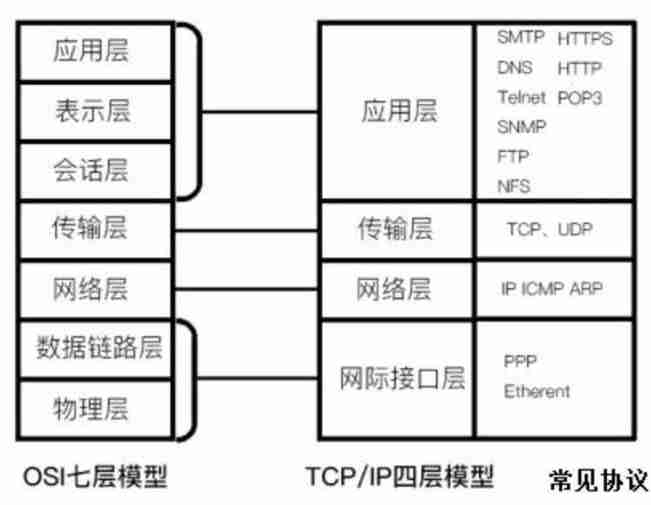
Concise words tell about technical people who must master basic IT knowledge and skills. Part 1
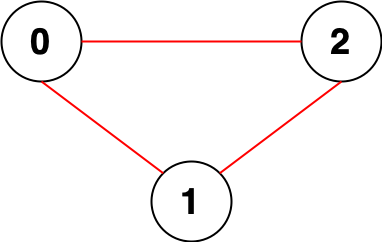
Leetcode counts the logarithm of points that cannot reach each other in an undirected graph

PMP项目管理概述

How does sound amplify weak sounds
mgalcu-a509

双击事件与单击事件的那些事

音响是如何把微弱声音放大呢
随机推荐
Oracle recovery tools actual batch bad block repair
Handling method of occasional error reporting on overseas equipment
allegro对走好的线取消走线的方法
Install mysql5.7 and change the password
Oracle Recovery Tools实战批量坏块修复
认证培训|StreamNative Certification 培训第2期
月薪没到30K的程序员必须要背的面试八股,我先啃为敬
Table implements alternative adaptation through pseudo classes
Three methods of time series prediction: statistical model, machine learning and recurrent neural network
安装mysql5.7 并修改密码
Matrix eigenvalue and eigenvector solution - eigenvalue decomposition (EVD)
PWN beginner level0
HashSet storing objects and how to not store the same objects
信息学奥赛一本通 1361:产生数(Produce)
allegro 设计中显示网络飞线或关闭网络飞线的方法
Only in the past four years, Microsoft finally gave it up!
PWN attack and defense world level2
Regular expression (?: pattern)
The 10 most commonly used gadgets for waterfall project management can be built and used freely
Sysbench Pressure Test Oracle (installation and use examples)
