当前位置:网站首页>[324. swing sequence II]
[324. swing sequence II]
2022-06-28 19:43:00 【Sugar_ wolf】
source : Power button (LeetCode)
describe :
Give you an array of integers nums, Rearrange it into nums[0] < nums[1] > nums[2] < nums[3]... The order of .
You can assume that all input arrays can get results that meet the requirements of the topic .
Example 1:
Input :nums = [1,5,1,1,6,4]
Output :[1,6,1,5,1,4]
explain :[1,4,1,5,1,6] It is also the result that meets the requirements of the topic , It can be accepted by the problem determination program .
Example 2:
Input :nums = [1,3,2,2,3,1]
Output :[2,3,1,3,1,2]
Tips :
- 1 <= nums.length <= 5 * 104
- 0 <= nums[i] <= 5000
- Topic data assurance , For a given input
nums, Always produce results that meet the requirements of the topic
Method 1 : Sort
Ideas and algorithms



Code :
class Solution {
public:
void wiggleSort(vector<int>& nums) {
int n = nums.size();
vector<int> arr = nums;
sort(arr.begin(), arr.end());
int x = (n + 1) / 2;
for (int i = 0, j = x - 1, k = n - 1; i < n; i += 2, j--, k--) {
nums[i] = arr[j];
if (i + 1 < n) {
nums[i + 1] = arr[k];
}
}
}
};
Execution time :8 ms, In all C++ Defeated in submission 99.09% Users of
Memory consumption :17.3 MB, In all C++ Defeated in submission 35.37% Users of
Complexity analysis
Time complexity : O(nlogn), among n Is the length of the array . The time complexity of array sorting is O(nlogn), The time complexity of traversing the array is O(n), The total time complexity is O(nlogn).
Spatial complexity : O(n), among n Is the length of the array . You need to copy the original array once , The space needed is O(n).
Method 2 : Three way syncopation
Ideas and algorithms




Code :
class Solution {
public:
void wiggleSort(vector<int>& nums) {
int n = nums.size();
int x = (n + 1) / 2;
int mid = x - 1;
nth_element(nums.begin(), nums.begin() + mid, nums.end());
for (int k = 0, i = 0, j = n - 1; k <= j; k++) {
if (nums[k] > nums[mid]) {
while (j > k && nums[j] > nums[mid]) {
j--;
}
swap(nums[k], nums[j--]);
}
if (nums[k] < nums[mid]) {
swap(nums[k], nums[i++]);
}
}
vector<int> arr = nums;
for (int i = 0, j = x - 1, k = n - 1; i < n; i += 2, j--, k--) {
nums[i] = arr[j];
if (i + 1 < n) {
nums[i + 1] = arr[k];
}
}
}
};
Execution time :16 ms, In all C++ Defeated in submission 75.61% Users of
Memory consumption :17.1 MB, In all C++ Defeated in submission 78.20% Users of
Complexity analysis
Time complexity : O(n), among n Is the length of the array . Found array sorted as k The time complexity required for the number of is O(n), The time complexity required for three-dimensional segmentation of an array is O(n), The time complexity of array placement is O(n), The total time complexity is O(n).
Spatial complexity : O(n), among n Is the length of the array . You need to copy the original array once , The space needed is O(n).
Method 3 : Index conversion
Ideas and algorithms



Code :
class Solution {
public:
inline int transAddress(int i, int n) {
return (2 * n - 2 * i - 1) % (n | 1);
}
void wiggleSort(vector<int>& nums) {
int n = nums.size();
int x = (n + 1) / 2;
int mid = x - 1;
nth_element(nums.begin(), nums.begin() + mid, nums.end());
int target = nums[mid];
for (int k = 0, i = 0, j = n - 1; k <= j; k++) {
if (nums[transAddress(k, n)] > target) {
while (j > k && nums[transAddress(j, n)] > target) {
j--;
}
swap(nums[transAddress(k, n)], nums[transAddress(j--, n)]);
}
if (nums[transAddress(k, n)] < target) {
swap(nums[transAddress(k, n)], nums[transAddress(i++, n)]);
}
}
}
};
Execution time :8 ms, In all C++ Defeated in submission 99.09% Users of
Memory consumption :16.8 MB, In all C++ Defeated in submission 90.93% Users of
Complexity analysis
Time complexity : O(n), among n Is the length of the array . Found array sorted as k The time complexity required for the number of is O(n), The time complexity required for three-dimensional segmentation of an array is O(n), The total time complexity is O(n).
Spatial complexity : O(logn). Find the first k Large elements require recursion , At this point, the space cost of recursion using stack space is expected to be O(logn).
Method four : Recursive optimization
Ideas and algorithms
On the basis of method 3, we can sort the search array to the No k The function of large elements is optimized , Use non recursive implementation to find the k Big elements , Further optimize the space complexity .
Code :
class Solution {
public:
int partitionAroundPivot(int left, int right, int pivot, vector<int> &nums) {
int pivotValue = nums[pivot];
int newPivot = left;
swap(nums[pivot], nums[right]);
for (int i = left; i < right; ++i) {
if (nums[i] > pivotValue) {
swap(nums[i], nums[newPivot++]);
}
}
swap(nums[right], nums[newPivot]);
return newPivot;
}
int findKthLargest(vector<int> &nums, int k) {
int left = 0, right = nums.size() - 1;
default_random_engine gen((random_device())());
while (left <= right) {
uniform_int_distribution<int> dis(left, right);
int pivot = dis(gen);
int newPivot = partitionAroundPivot(left, right, pivot, nums);
if (newPivot == k - 1) {
return nums[newPivot];
} else if (newPivot > k - 1) {
right = newPivot - 1;
} else {
left = newPivot + 1;
}
}
return nums[k - 1];
}
inline int transAddress(int i, int n) {
return (2 * n - 2 * i - 1) % (n | 1);
}
void wiggleSort(vector<int>& nums) {
int n = nums.size();
int x = (n + 1) / 2;
int mid = x - 1;
int target = findKthLargest(nums, n - mid);
for (int k = 0, i = 0, j = n - 1; k <= j; k++) {
if (nums[transAddress(k, n)] > target) {
while (j > k && nums[transAddress(j, n)] > target) {
j--;
}
swap(nums[transAddress(k, n)], nums[transAddress(j--, n)]);
}
if (nums[transAddress(k, n)] < target) {
swap(nums[transAddress(k, n)], nums[transAddress(i++, n)]);
}
}
}
};
Execution time :168 ms, In all C++ Defeated in submission 11.66% Users of
Memory consumption :16.9 MB, In all C++ Defeated in submission 86.81% Users of
Complexity analysis
Time complexity : O(n), among n Is the length of the array . Found array sorted as k The time complexity required for the number of is O(n), The time complexity required for three-dimensional segmentation of an array is O(n), The total time complexity is O(n).
Spatial complexity : O(1).
边栏推荐
- 1002_ twenty million one hundred and eighty-one thousand and nineteen
- MDM data analysis function description
- Design of secsha system
- 数字经济专家高泽龙:映客更名映宇宙,元宇宙会成为映客下一个增长引擎吗?
- 2280.Cupboards
- 视差js特效js轮播图插件
- C#应用程序界面开发基础——窗体控制
- 严重性 代码 说明 项目 文件 行 禁止显示状态 错误 C1047 对象或库文件“.lib”是使用与其他对象(如“x64\Release\main.obj”)不同的
- 道路千万条,为什么这家创新存储公司会选这条?
- Matlab 2D or 3D triangulation
猜你喜欢
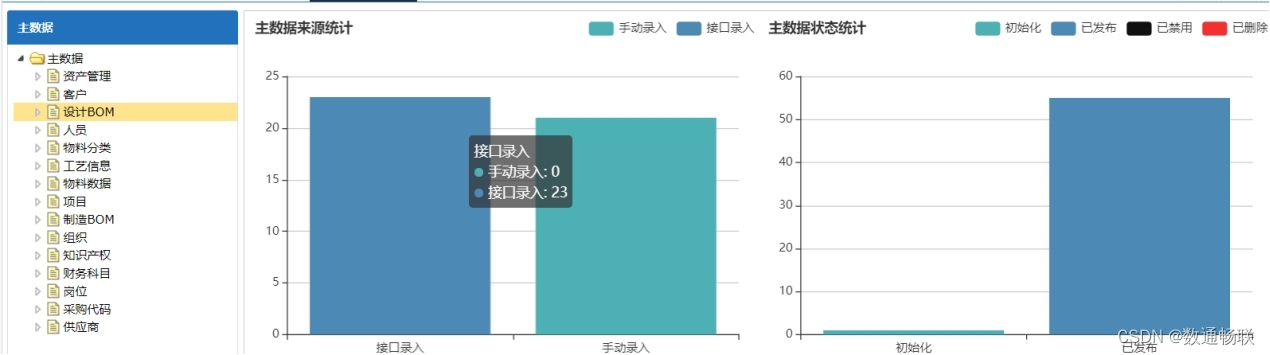
MDM data analysis function description

数论 --- 欧拉函数、筛法求欧拉函数、欧拉定理、费马小定理详细证明

论文3 VScode&texlive&SumatraPDF打造完美书写论文工具
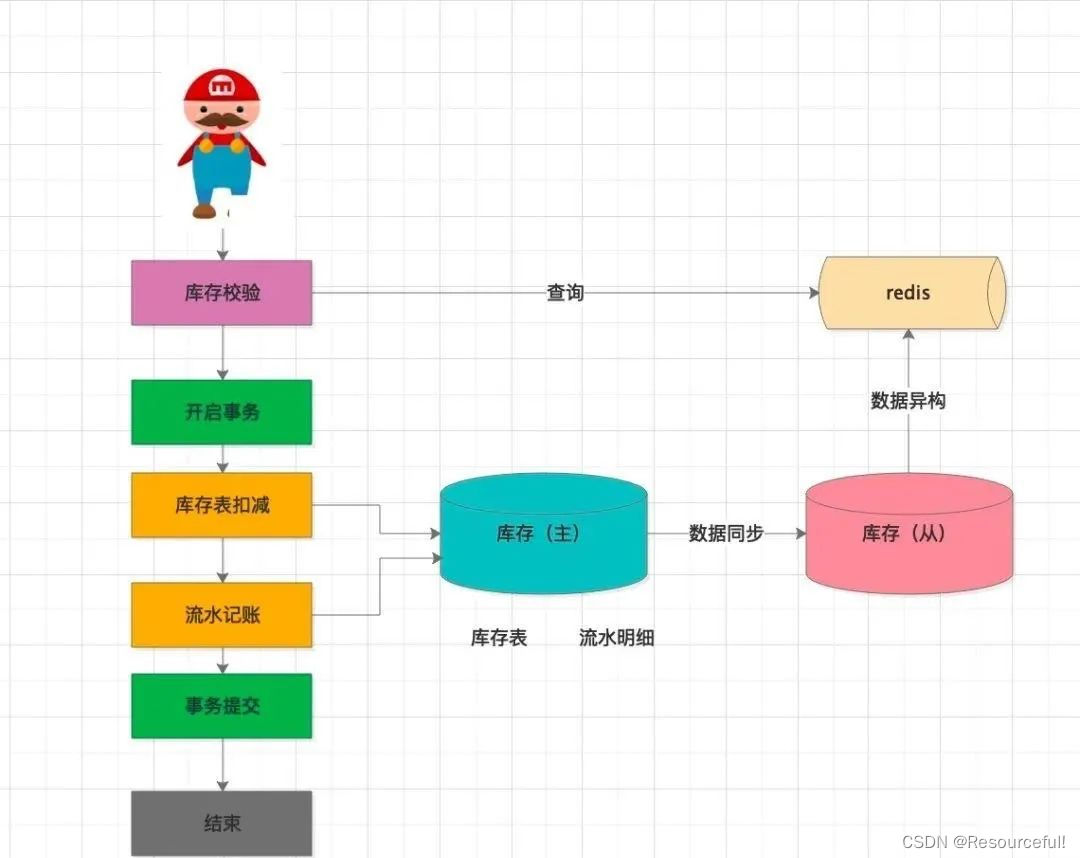
How does redis implement inventory deduction? How to prevent oversold?

Demo of intelligent computing system 2 bangc operator development (heterogeneous programming flow of CPU and mlu270)

《数字经济全景白皮书》消费金融数字化篇 重磅发布

How to learn JS through w3school / how to use the JS reference manual of w3school

PCL 环境下安装配置CGAL 5.4.1

使用点云构建不规则三角网TIN

《数据安全法》出台一周年,看哪四大变化来袭?
随机推荐
There are thousands of roads. Why did this innovative storage company choose this one?
The amazing nanopc-t4 (rk3399) is used as the initial configuration and related applications of the workstation
R语言GLM广义线性模型:逻辑回归、泊松回归拟合小鼠临床试验数据(剂量和反应)示例和自测题
Industry analysis - quick intercom, building intercom
Bayesian inference problem, MCMC and variational inference
Facts / assertions / assertions / conclusions / assertions / judgments
The first meta universe concept novel, meta universe 2086, won the upper attack meta universe award in 2022
Redis 如何实现库存扣减操作?如何防止商品被超卖?
内核错误怎么解决?Win11系统内核错误解决方法
In which industries did the fire virtual human start to make efforts?
《数据安全法》出台一周年,看哪四大变化来袭?
Design of secsha system
2788.Cifera
易观分析《2022年中国银行业隐私计算平台供应商实力矩阵分析》研究活动 正式启动
颜色渐变的FontAwesome图标
Nanopc-t4 (rk3399) Game1 OLED (I2C) display time weather temperature
Average score of 100 people
Number theory -- detailed proof of Euler function, sieve method for Euler function, Euler theorem and Fermat theorem
【324. 摆动排序 II】
秋招经验分享 | 银行笔面试该怎么准备