leetcode：210. Schedule II

Title source

• leetcode

Title Description

title

Only directed acyclic graphs have topological order

Topological sorting is not a pure sorting algorithm , It is only for a class of graphs , Find a linear order that can be executed .

For what kind of graph ？ Directed acyclic graph . Even if ：

• The edges of this graph must be directional ;
• There is no ring in the picture .

So what is the direction ？

For example, wechat friends are targeted , You add his friend, he may delete you, but you don't know ... Then the friendship is one-way ..

What is a ring ？ Rings are about direction , Starting from a point, you can go back to yourself , This is the ring .

So the left side of the picture is not a ring , On the right is .

So if a graph has rings , For example, on the right , Want to execute 1 You have to do it first 3, Want to execute 3 You have to do it first 2, Want to execute 2 You have to do it first 1, It's a dead circle , Can't find the right way to open , So we can't find a topological order of it .

Conclusion ：

• If this is not DAG, So it has no topological order ;
• If it is DAG, So it has at least one topological order ;
• conversely , If it has a topological order , So this picture must be DGA.

For this question , Topological sorting means ： Solve a feasible sequence , Let me learn all the lessons .

So how do you do that ？

（1） First, we can describe it with a diagram , The two elements of a graph are Vertices and edges , So here ：

• The vertices ： Every course
• edge ： The starting course is the prerequisite of the end course

Suppose there is a graph like this ：

This kind of picture is called AOV(Activity On Vertex) The Internet , In this picture ：

• The vertices ： It means activity ;
• edge ： Show the sequence of activities

So a AOV The net should be a DAG, The directed acyclic graph , Otherwise, some activities will not be carried out .

Then all activities can be arranged into a feasible linear sequence , This sequence is the topological sequence .

So the actual meaning of this sequence is ：

In this order , At the beginning of each project , To ensure that all its precursor activities have been completed , So that the whole project can proceed smoothly .

Back to our example ：

• We can see at a glance that we need to learn C1, C2, Because there are no requirements for these two courses , I learned it when I was a freshman ;
• Sophomore can learn the second line C3, C5, C8 了 , Because the prerequisite of these three courses is C1, C2, We've all finished learning ;
• Junior can learn the third line of C4, C9;
• In the last year, choose the rest C6, C7.

such , We'll finish all the courses , So we get a topological sort of this graph .

Be careful , Sometimes the topological order is not unique , For example, in this case , Learn first C1 Learn again C2, And first C2 after C1 Will do , All are the correct topological order of the graph , But these are two orders .

So when interviewing, ask the following examiners , It's asking for an arbitrary solution , Or list all the solutions .

The edge in this graph represents a dependency , If you want to take the next course , I'm going to take the previous course first

It's the same as playing games , To get a prop , Just do it first A Mission , Finish again B Mission , Finally, we can reach our destination .

In the picture above , You can easily see its topological order , But as the project gets bigger and bigger , Dependency relationships can also become complicated , Then we need to solve it in a systematic way .

So let's think back to the process of finding topological order by ourselves , Why did we take a fancy to C1, C2?

Because they don't depend on others , That is, its penetration is 0.

• The degree of ： The penetration of a vertex is 「 The edge that points to the vertex 」 The number of ;
• The degree of ： The outdegree of a vertex is the number of edges that the vertex points to other points .

So let's do it first 0 Those points of , So we First record the depth of each vertex . Because only when its depth is 0 When , We can carry it out .

In the example just now , In the beginning C1, C2 It's just that 0, So we can do these two first .

In this algorithm, the first step is to get the degree of each vertex .

（1） Preprocessing gets the degree of penetration of each point

We can use one HashMap To store this information , Or it would be more sophisticated to use an array .

When you get this , You can execute the degree of 0 These are the points of , That is to say C1, C2.

So let's take the points that can be implemented , Put one in In the container to be executed , After that, we can take the vertices from this container one by one .

As for which data structure the container chooses , It depends on what we need to do , Let's look at which data structure can serve it .

Well, first of all, you can put **[C1, C2]** Put it in a container ,

Then think about what we need to do ！

What we do most often is Put the dots in , Take the point out and execute , So you can use a queue

Anything else will do , The vertices put into this container have the same status , It's all executable , It has nothing to do with the order in which they came in , But why bother yourself ？ Simple in a regular order queue That's enough. .

Then you need to take some points out and execute .

When we put C1 Take it out and carry it out , So what does this mean ？

answer ： signify 「 With C1 For the top 」 Of 「 Point to other points 」 Of 「 edge 」 All disappeared. , That is to say C1 It's become 0.

Here's the picture , That is, these two edges can disappear .

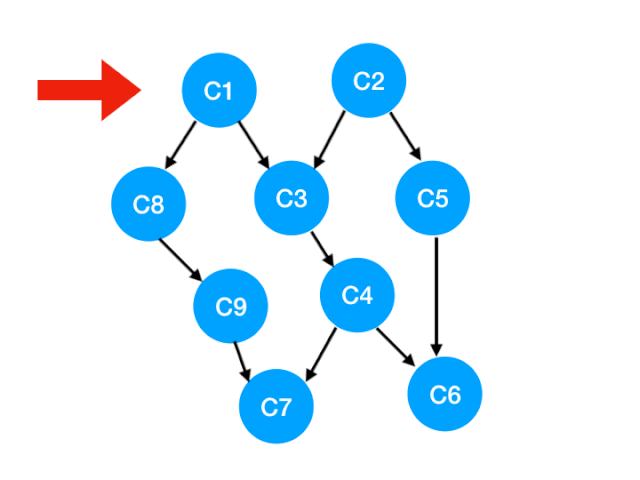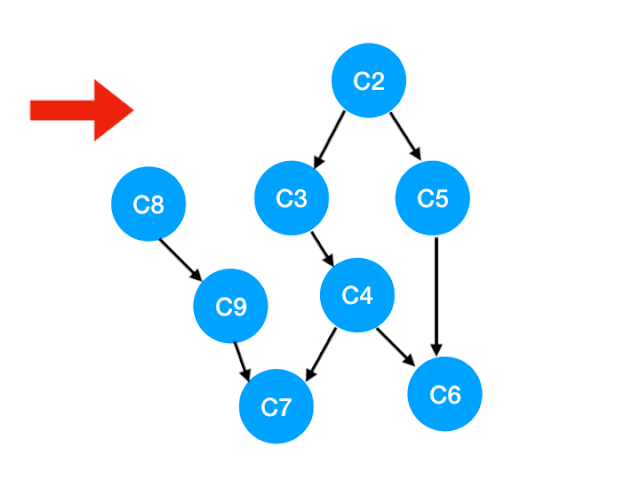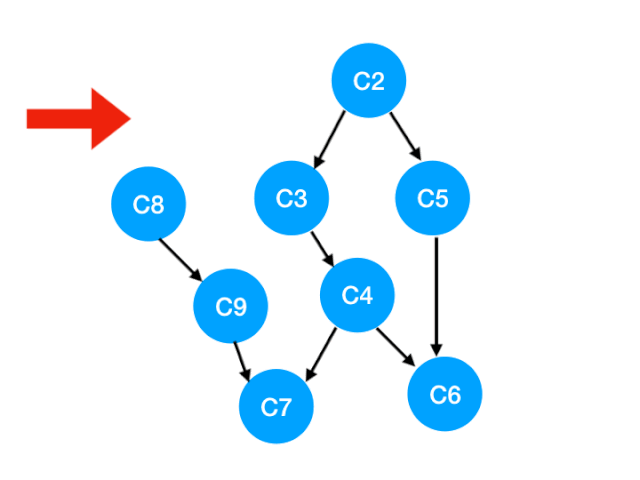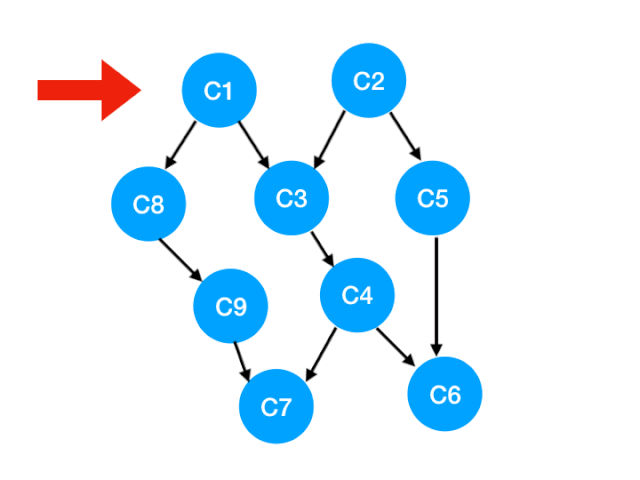
Then we can update C1 The points pointed to are C3 and C8 Of The degree of 了 , The updated array is as follows ：

So we see a crucial step here ,C8 It becomes 0！

That means C8 There is no dependence at this time , You can put it in our queue It's waiting to be carried out .

Now our queue Inside is ：[C2, C8].

We'll do it next C2

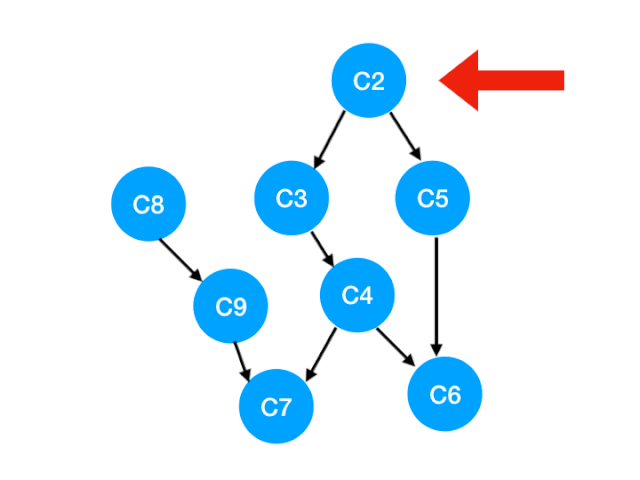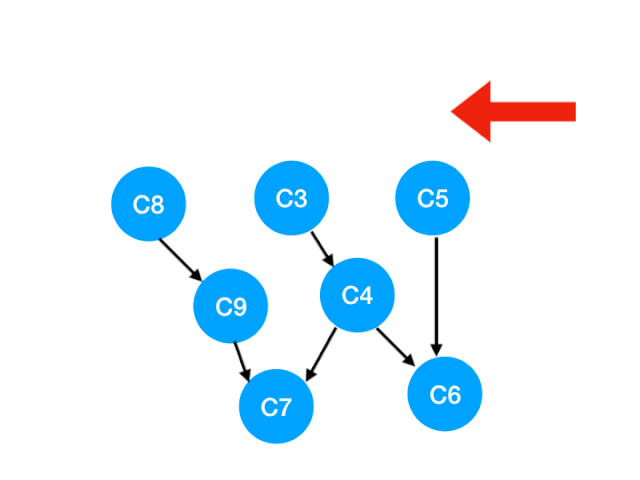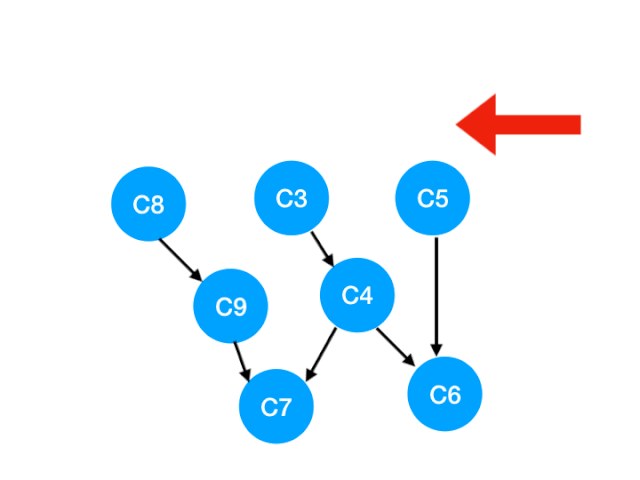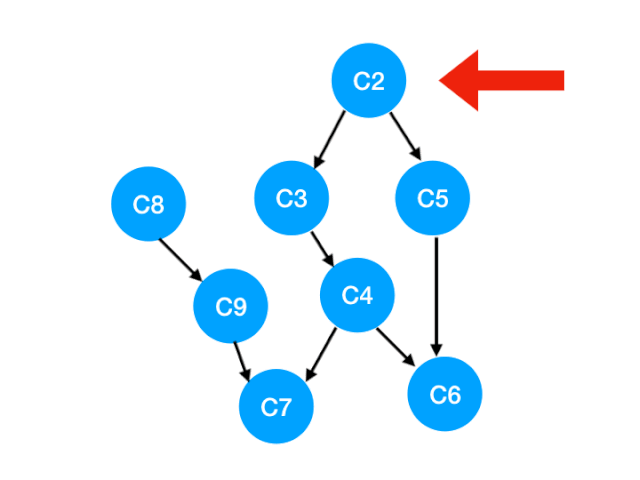
that C2 The point is C3, C5 Of The degree of -1,

Update Form ：

That is to say C3 and C5 There's no bondage , You can put in queue Li implemented. .

queue It becomes ：[C8, C3, C5]
So the next step is to implement C8

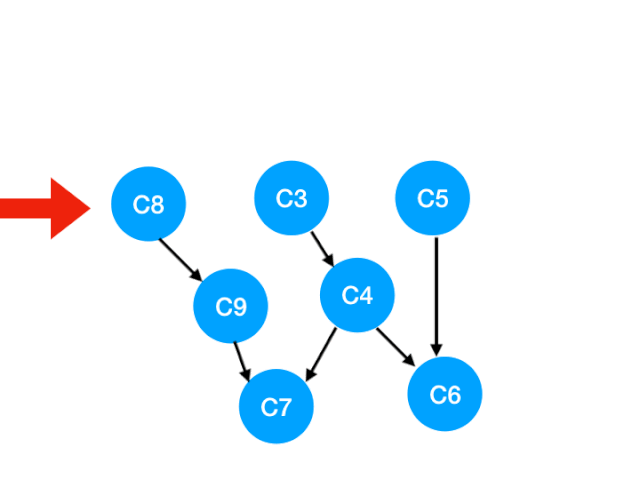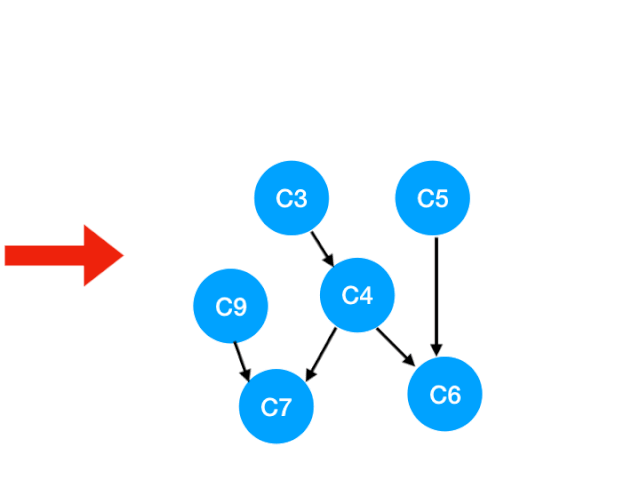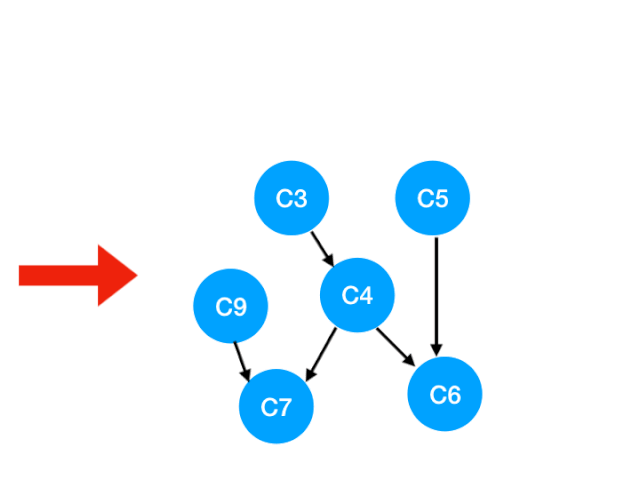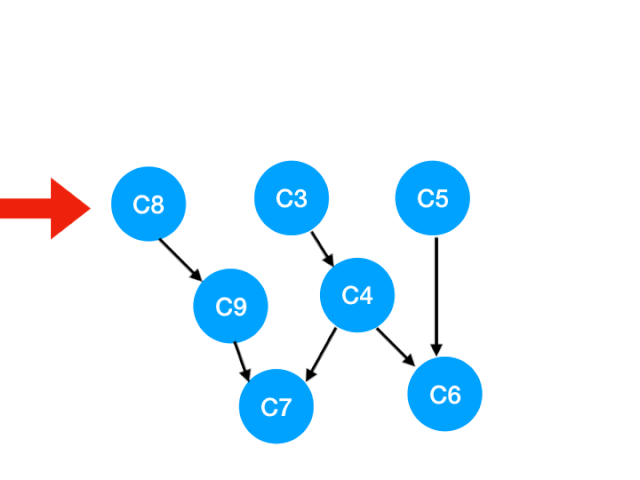
Corresponding C8 Referred to C9 The degree of -1. Update Form ：

that C9 There's no requirement , You can put in queue Li implemented. .

queue It becomes ：[C3, C5, C9]

Next C3,

Corresponding C3 Referred to C4 The degree of -1. Update Form ：

however C4 It doesn't become 0, So there's no point in this step queue.

queue It becomes [C5, C9]

Re execution C5

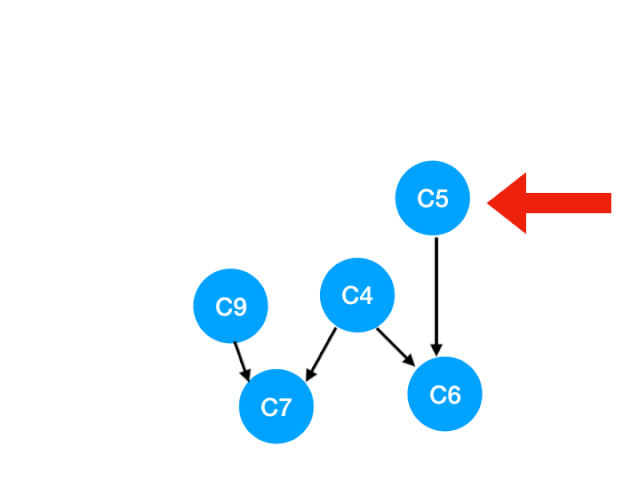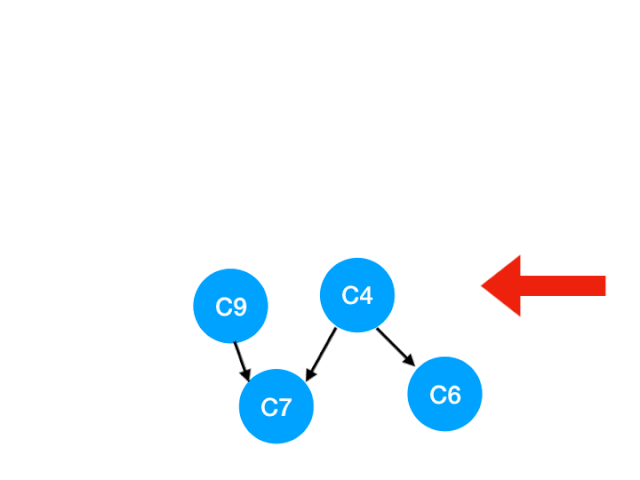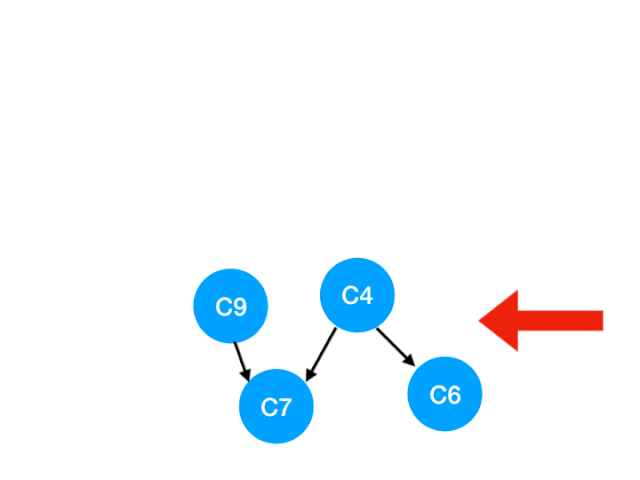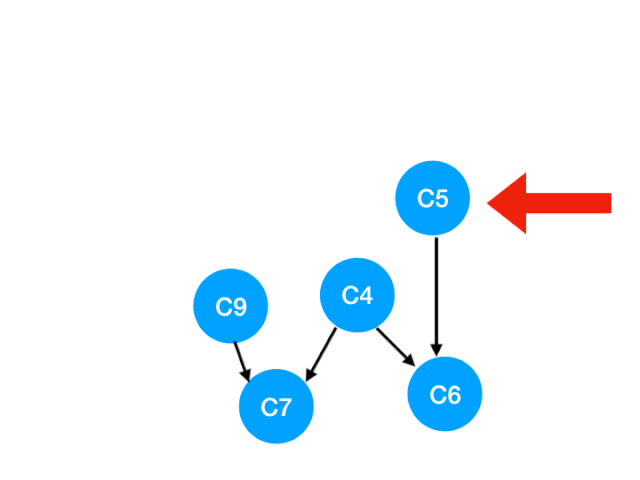
that C5 Referred to C4 and C6 The degree of - 1. Update Form ：

here C4 All of our dependence has disappeared , So you can take C4 In the queue In the ：

queue = [C9, C4]

Step6

And then execute C9

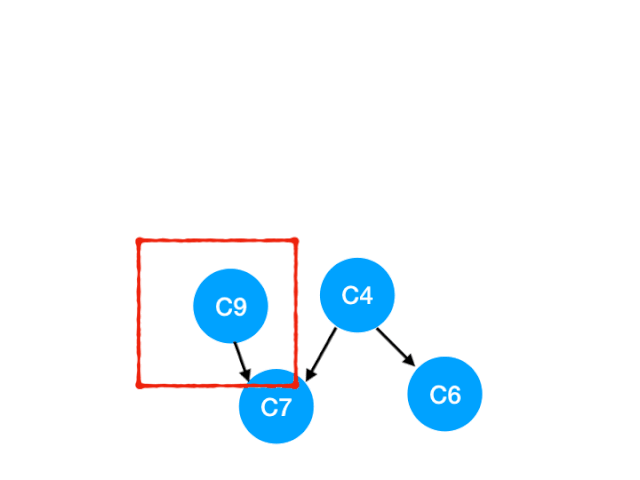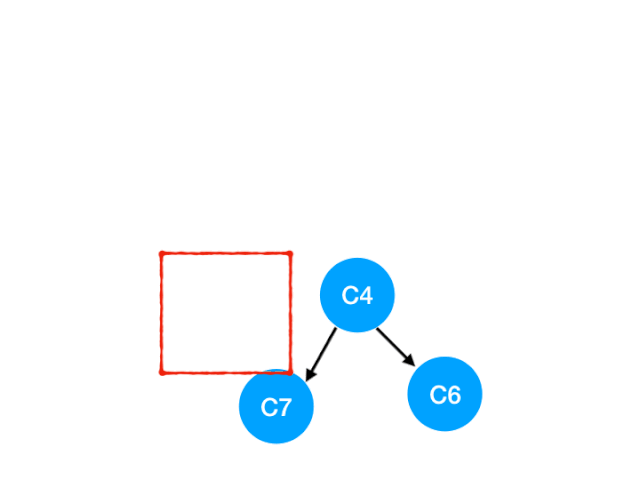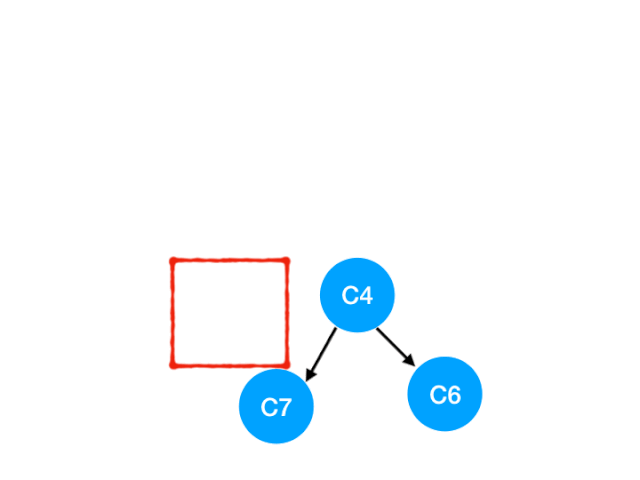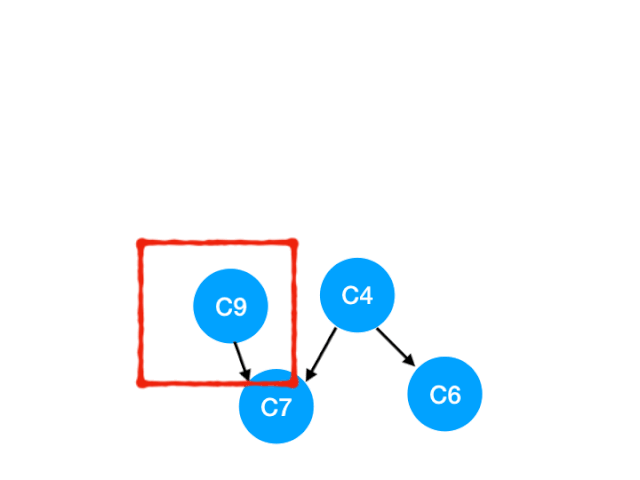
that C9 Referred to C7 The degree of - 1

here C7 It's not for 0, Can't join in yet queue,

here queue = [C4]
Then perform C4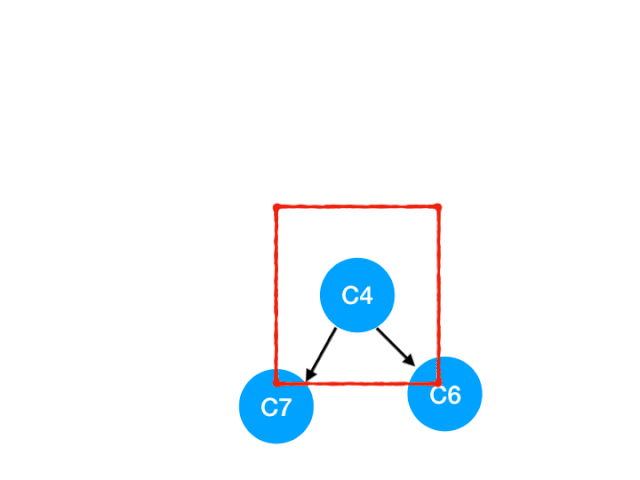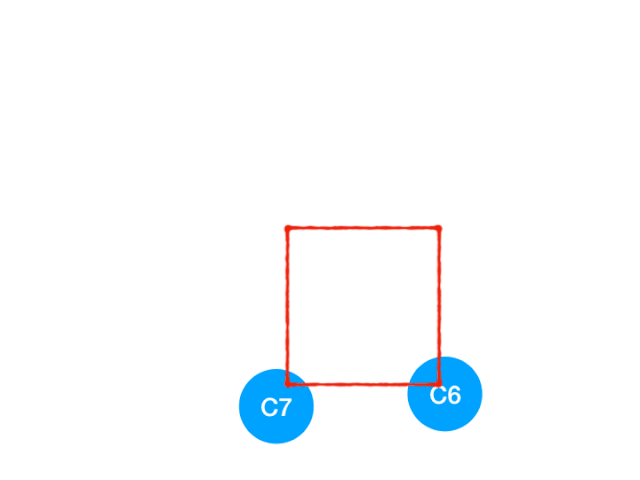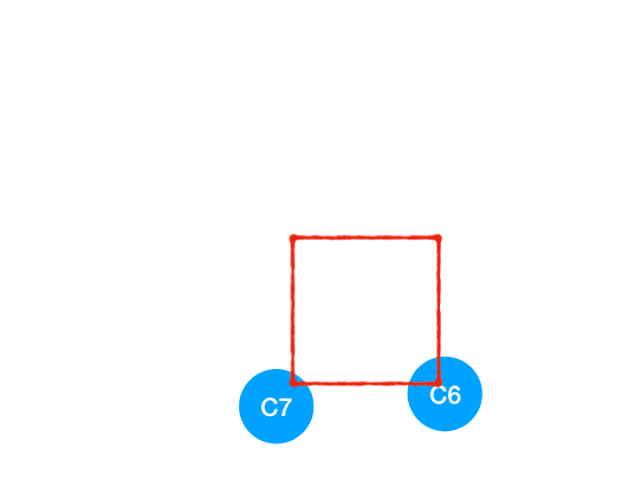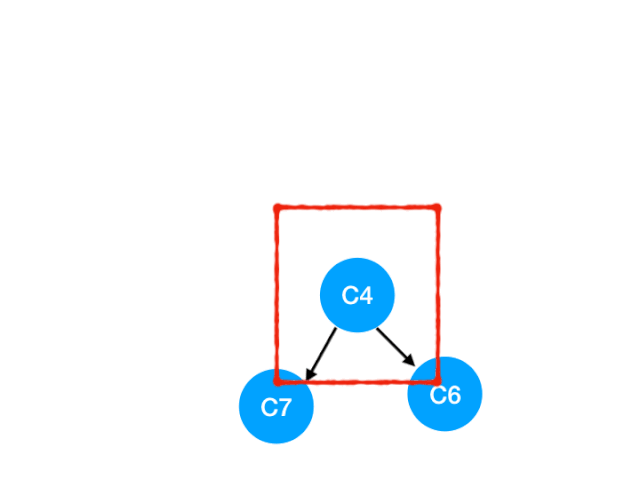

therefore C4 The point is C6 and C7 The degree of -1, Update Form ：

C6 and C7 It's like 0 La ！！ Put them in queue, Continue until queue If it is empty, you can

Time complexity

Spatial complexity