当前位置:网站首页>games202:三,实时环境光照IBL + PRT
games202:三,实时环境光照IBL + PRT
2022-08-02 10:12:00 【我要吐泡泡了哦】
games202:三,实时环境光照IBL + PRT
一,IBL(image-based lighing)
- IBL应用条件:假设光源无限远(当光源和物体有确定的距离的时候就不能用了)
1.0 漫反射部分:球谐光照
这里的内容老师放到后边专门讲了,见第四部分。
1.1 镜面反射部分:Split-Sum近似
环境光照和直接光照的渲染方程是一样的,熟悉的渲染方程:

由于公式里的BRDF项在光滑材质上只对镜面方向反射、在粗糙材质上对各个方向均匀反射(均匀=积分域smooth),这里之前数学课(L3)上讲到的积分近似公式就派上用场(积分域比较小或者smooth的情况下,该近似比较准确----这不是巧了吗):

带入渲染方程得到下式:
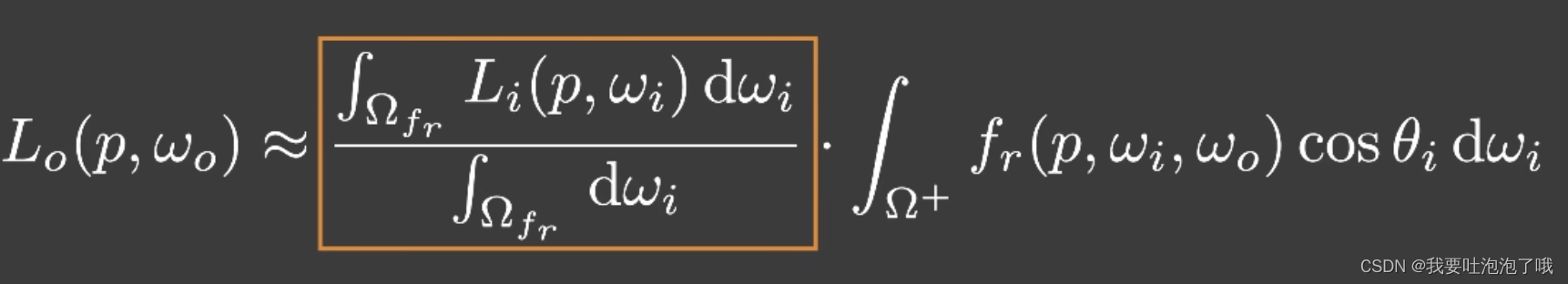
「注意:阴影用了同一个公式但是拆解出来的是可见性项,可以灵活运用
」Split-Sum近似(求和与积分的区别):
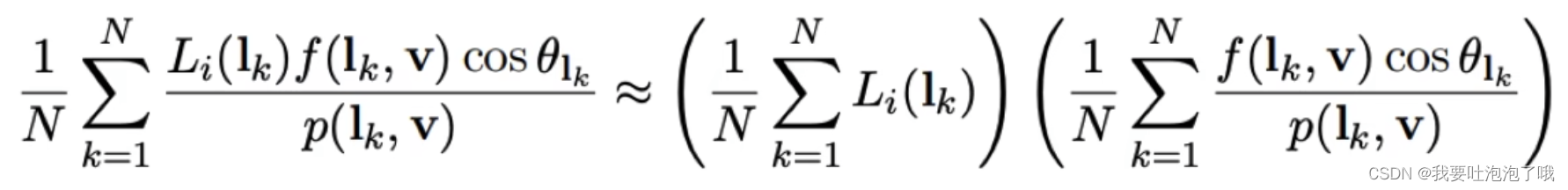
由上,咱们镜面反射部分的渲染方程可以被写作:
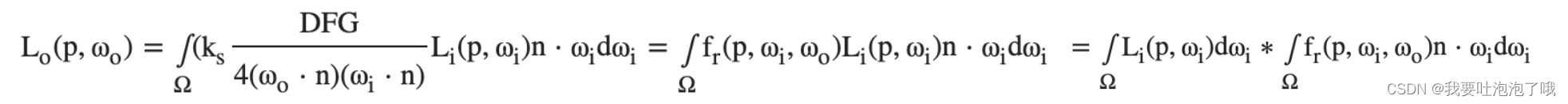
这样就拆分为了光亮度的均值和环境 BRDF两项,然后对两项分别进行离线预计算。
1.1.1 第一项:预滤波环境贴图
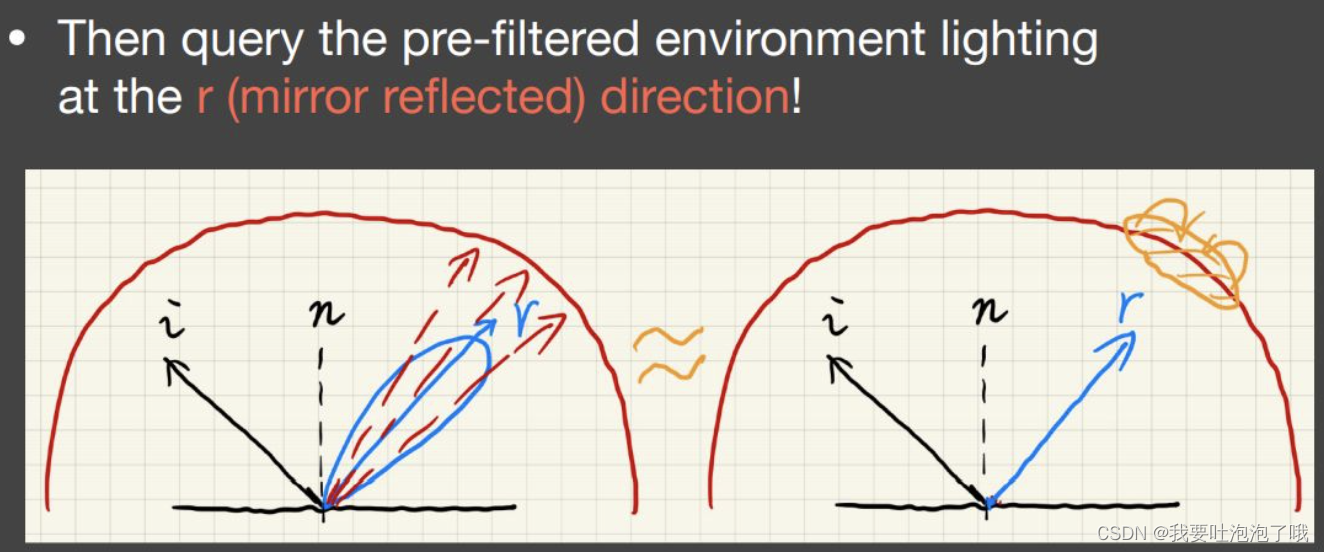
- 如果想要算出精确的lightling项,需要在BRDF的lobe(反射波瓣)区域采样后做平均,但先采样后平均≈先平均后采样,因此我们进行先平均(模糊)后采样的操作。
- 具体到渲染器里就是对环境贴图模糊处理,越粗糙积分域越大越模糊(即cubemap mipmap);这个操作可以在渲染之前就完成,在渲染器里就是预滤波Prefiltering;不同模糊等级的mipmap用BRDF来确定(实际用粗糙度),通过三线性插值取两个mipmap之间的结果。
- tips:
- 这里是在对球面做滤波,因此对贴图做滤波的核的大小的单位是立体角。
- 漫反射diffuse其实也相当于对整个环境贴图做平均(沿normal方向),但在真正实现的时候我们会对duffuse单独处理,见第四部分球谐光照,所以不用考虑它。
1.1.2 第二项:BRDF预计算
- 真正计算BRDF项时至少涉及5个维度----粗糙度, r, g, b, 角度
- 在101中我们学过菲涅尔项的Schlick近似写法和NDF的Beckmann描述:
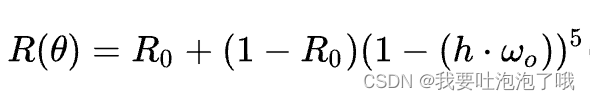

- 由于在实时渲染中,入射反射夹角和入射半角夹角近似相等, θ h θ_h θh又可以通过这三个角度计算得到,因此可以看成是一个角维度,再加上粗糙度、R0(F0),一共三个维度。
- 这时再把菲涅尔项的Schlick近似带入原式,发现分解成了F0 * Scale + Offset的形式:

- 由于F0在实际操作中可以看为常数,因此这时就剩两个维度了,F0和粗糙度,把它预计算出来:
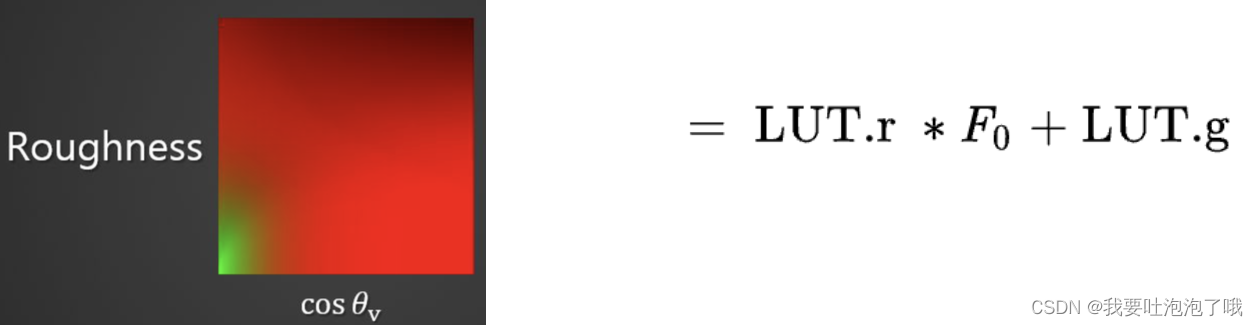
二,环境光照阴影问题现状
- 知道环境光后该如何生成环境光下的阴影呢?遗憾的是,并没有特别好的解决办法,很难得到。原因有二:
- 如果把环境光理解为非常多个小的多光源,shadowmap的数量线性增加……
- 如果通过采样去计算环境光下的可见性,只能盲采–数量累加质量;同时上边说的split sum近似方法需要在积分域很小或者足够smooth的时候才成立,这时如果盲采visibility的话积分域就变成了半球,如果是光滑材质就不符合split sum的使用条件,因此不能在公式里提取visibility。
「在有constant environment lighting的时候(全白或全黑),可以使用AO环境光遮蔽简单代替环境光阴影,其他情况AO不准」
- 工业界做法:只生成最大的环境光光源(如太阳)的阴影
- 其他环境光阴影的相关研究:
- Imperfect shadow maps:全局光照阴影的一个解决方案
- Light cuts:是离线渲染中,把场景中的反射无当做小的光源,然后通过归类得到近似结果(Offline中的many-light问题)
- real-time ray tracing(RTRT):可能是环境阴影的终极解决方案
- Precomputed radiance transfer(PRT):可以准确的得到环境阴影的结果,但要付出代价……
「通常工业游戏引擎不会只使用上边某一种方案,而是会把好几种方案大杂烩的放在一块----UE5洞穴」
三,PRT前置数学知识
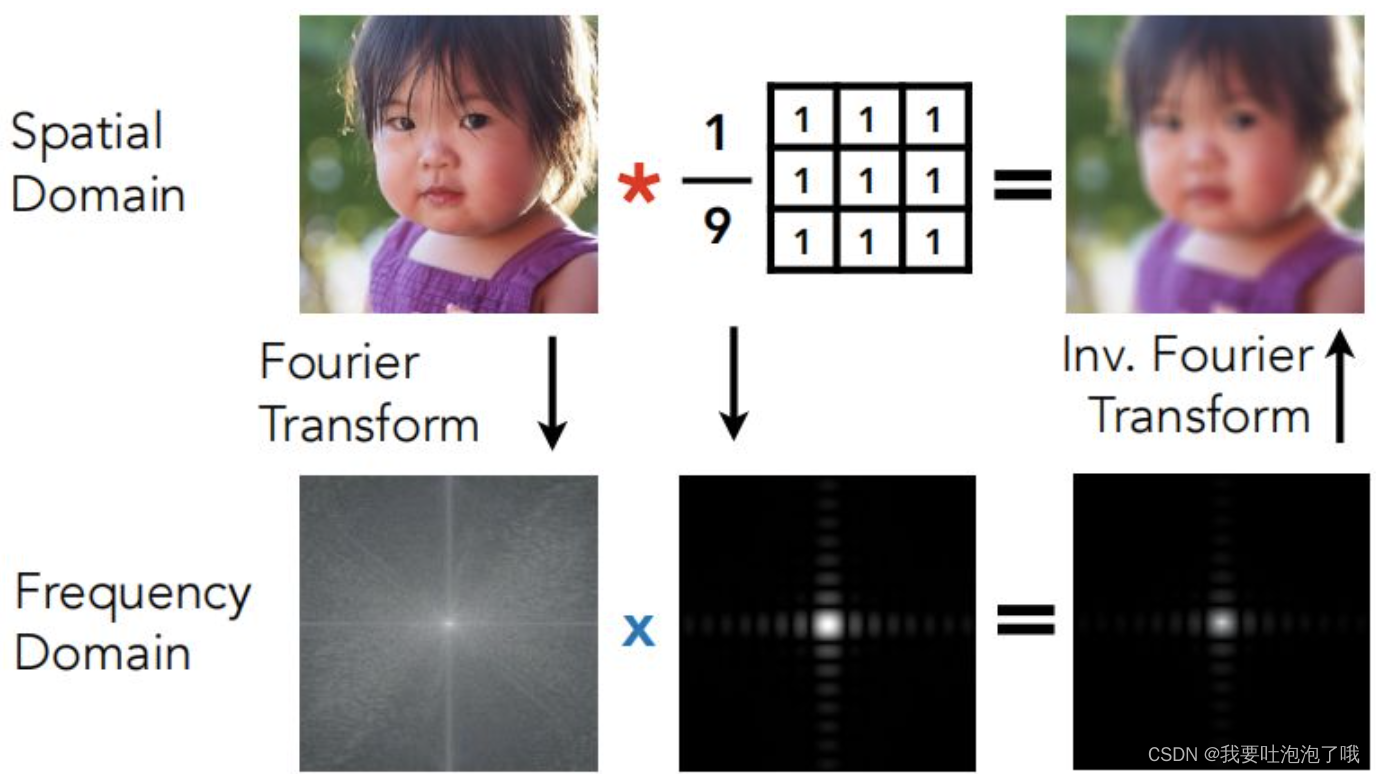
- 傅里叶级数展开:周期函数都可以代替为sin和cos的线性表达式,本质是图从时域(空间域)到频域的变换,见下左图。
f ( x ) = A 2 + 2 A c o s ( t ω ) π − 2 A c o s ( 3 t ω ) 3 π + 2 A c o s ( 5 t ω ) 5 π − 2 A c o s ( 7 t ω ) 7 π + … … f(x) = \frac{A}{2} + \frac{2Acos(tω)}{π} - \frac{2Acos(3tω)}{3π} + \frac{2Acos(5tω)}{5π} - \frac{2Acos(7tω)}{7π} + …… f(x)=2A+π2Acos(tω)−3π2Acos(3tω)+5π2Acos(5tω)−7π2Acos(7tω)+…… - 基函数(Basis Functions):一个函数可以描述为其他一系列基函数的组合,即 f ( x ) = ∑ c i ⋅ B i ( x ) f(x) = \sum{c_i \cdot B_i(x)} f(x)=∑ci⋅Bi(x)中的 B i ( x ) B_i(x) Bi(x)
- 滤波Filtering-----去掉一系列频率上的图像内容:时域上做卷积(模糊)就相当于在频域上做乘积(通过傅里叶变化转换),公式为 ∫ Ω f ( x ) g ( y ) d x \int_{Ω}{f(x)g(y)dx} ∫Ωf(x)g(y)dx,流程见下右图。
「把两个函数相乘后积分的操作认为是滤波操作,相乘后积分的结果的频率是由两个函数更低频的一方决定的。」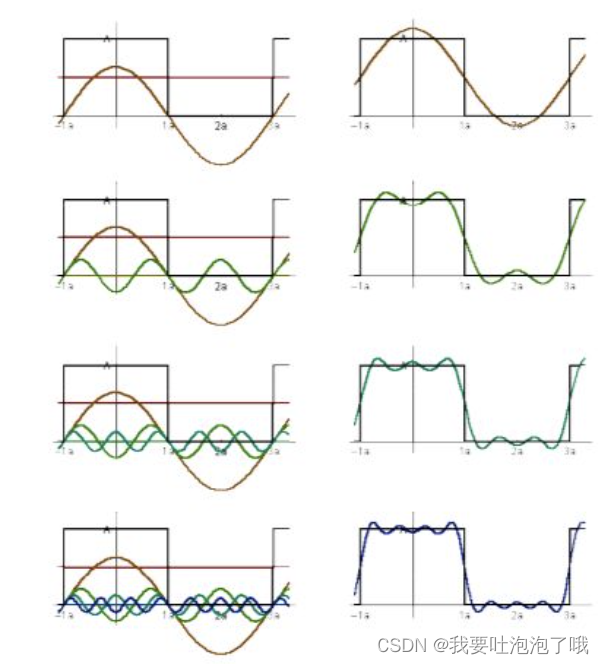
四,球谐函数SH(Spherical Harmonics)
4.1 球谐函数含义
- 如同傅里叶变换可以用基函数表达周期函数,三维函数也可以用基函数表达;而球谐函数本质上就是3维球面坐标系下的二维基函数。「球面坐标系–> r 0 = f 0 ( θ , ψ ) r_0 = f_0(θ,ψ) r0=f0(θ,ψ)」
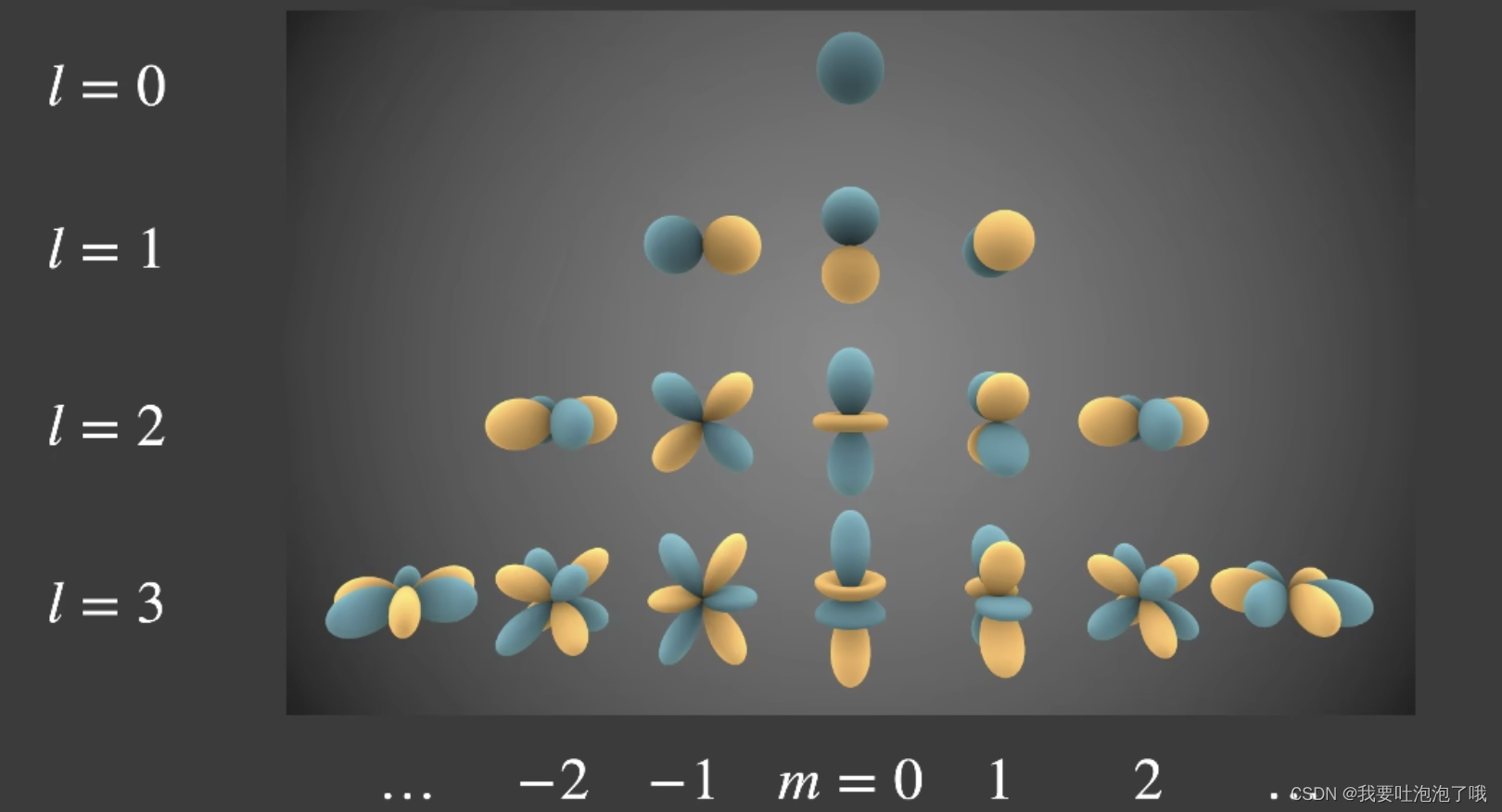
- 下图就是球谐函数的可视化图。其中l表示阶数(代表频率不同),每阶有2l+1个基函数,前n阶共有 n 2 n^2 n2个;m表示序号,从-l到l;过取n阶球谐函数表达球面。
- 蓝色表示正数,黄色表示负数,颜色深浅表示值大小,越深越小;形状表示频率大小;
- tips:为什么不把环境贴图做二维傅里叶展开呢?----因为前边讲过了,这是对球面做展开,每个单位应该代表的面积/角度相同,即立体角。
4.2 SH使用–环境漫反射
- 每一个基函数都可以由 勒让德多项式(Legendre) 写出来,该多项式非常复杂,不用细看,总之就是各项表达式都已知;由 f ( x ) = ∑ c i ⋅ B i ( x ) f(x) = \sum{c_i \cdot B_i(x)} f(x)=∑ci⋅Bi(x)可以看出,只要得到 c i c_i ci组成的i维向量 ( c 1 , c 2 , … , c i ) (c_1,c_2,…,c_i) (c1,c2,…,ci)(球谐系数)就可以表达函数 f ( x ) f(x) f(x)
- 投影(与坐标系一模一样):通过滤波原理计算球谐系数,方便重建原函数,公式为 c i = ∫ Ω f ( x ) B i ( x ) d x c_i = \int_{Ω}{f(x)B_i(x)dx} ci=∫Ωf(x)Bi(x)dx用的基函数越多重建细节越多。「推导:公式 f ( x ) = ∑ c i ⋅ B i ( x ) f(x) = \sum{c_i \cdot B_i(x)} f(x)=∑ci⋅Bi(x)两边同乘 B i ( x ) B_i(x) Bi(x)然后做积分,根据正交原理,右边剩 c i c_i ci」

「当描漫反射光照一般用到第3阶(9个基函数对应27个rgb信息),如果使用高阶SH由于其物理含义会出现一些Artifact(美术眼中的bug)」 - 在前边讲镜面部分的lighting“预滤波环境贴图”时提到过,「diffuse其实相当于对整个环境贴图做平均,但实际中有专门的的处理方式」,这个处理方式就是利用球面谐波函数对环境贴图展开近似,并取其低阶基函数(diffuse本身就是低频信息,这里的低频指颜色变化不剧烈),这样就可以用储存好的27个向量代替采样了。正如下图所描述的。


4.3 SH性质
- 正交性,每个基函数都相互正交,任意基函数向另一个的投影为0,向自己投影为1:
∫ Ω B i ( i ) ⋅ B j ( i ) d i = 1 , ( i = j ) \int_{Ω}B_i(i) \cdot B_j(i) di =1,(i=j) ∫ΩBi(i)⋅Bj(i)di=1,(i=j) ∫ Ω B i ( i ) ⋅ B j ( i ) d i = 0 , ( i ≠ j ) \int_{Ω}B_i(i) \cdot B_j(i) di =0,(i≠j) ∫ΩBi(i)⋅Bj(i)di=0,(i=j) - 旋转不变性:旋转任意基函数,该基函数还能被同阶的其他基函数线性表达出来(系数变了)。同理如果旋转光照,就相当于旋转所有基函数,而只修改原基函数的线性系数就可以得到,马上可以继续使用。这意味着一组sh可以表达任意旋转的光照。
五,基于预计算的辐射传输PRT(Precompute Radiance Transfer)
- PRT基本思路:假设shading point渲染方程里的可见性和brdf项都是不变的(只在景静物场景下成立),只有光照会旋转或更换;因此把光照分为2部分,一是lighting,二是light transport;这样lighting部分旋转不影响球谐函数使用、更换只需预计算时多计算其他光源即可,因此lighting和light transport就都可以被球谐函数表示,可以预计算了。
L ( o ) = ∫ Ω L ( i ) V ( i ) f r ( i , o ) m a x ( 0 , n ⋅ i ) d i = ∫ Ω L ( i ) ⋅ T ( i , o ) d i L(o) = \int_{Ω}L(i)V(i) f_r(i,o)max(0,n \cdot i) di = \int_{Ω}L(i) \cdot T(i,o)di L(o)=∫ΩL(i)V(i)fr(i,o)max(0,n⋅i)di=∫ΩL(i)⋅T(i,o)di
5.1 diffuse case
5.1.1 计算方法1
diffuse 场景下brdf为常数,将 L ( i ) ≈ ∑ l i B i ( i ) L(i) ≈ \sum l_iB_i(i) L(i)≈∑liBi(i) 代入 L ( o ) = ρ ∫ Ω L ( i ) V ( i ) m a x ( 0 , n ⋅ i ) d i L(o) = ρ \int_{Ω}L(i)V(i) max(0,n \cdot i) di L(o)=ρ∫ΩL(i)V(i)max(0,n⋅i)di 得到(积分求和顺不顺序的实时渲染不在乎) :
L ( o ) ≈ ρ ∑ l i ∫ Ω B i ( i ) V ( i ) m a x ( 0 , n ⋅ i ) d i L(o) ≈ ρ \sum l_i \int_{Ω}B_i(i)V(i) max(0,n \cdot i) di L(o)≈ρ∑li∫ΩBi(i)V(i)max(0,n⋅i)di
对这个式子有两种理解方式:
- 其中的 ∫ Ω B i ( i ) V ( i ) m a x ( 0 , n ⋅ i ) d i \int_{Ω}B_i(i)V(i) max(0,n \cdot i) di ∫ΩBi(i)V(i)max(0,n⋅i)di不就是light transport在球谐函数上投影的系数吗,因此可以对这个部分做一个预计算,得到一个向量 T i T_i Ti,最终公式变为 L ( o ) ≈ ρ ∑ l i T i L(o) ≈ ρ \sum l_i T_i L(o)≈ρ∑liTi,即两个向量的点乘,即light transport在SH上投影的系数 点乘 lighting在SH上投影的系数。
- 也可以把这里的每个基函数 B i ( i ) B_i(i) Bi(i)都理解为一个光源,然后用i个环境光的结果以 l i l_i li为权重累加求和。如下图。
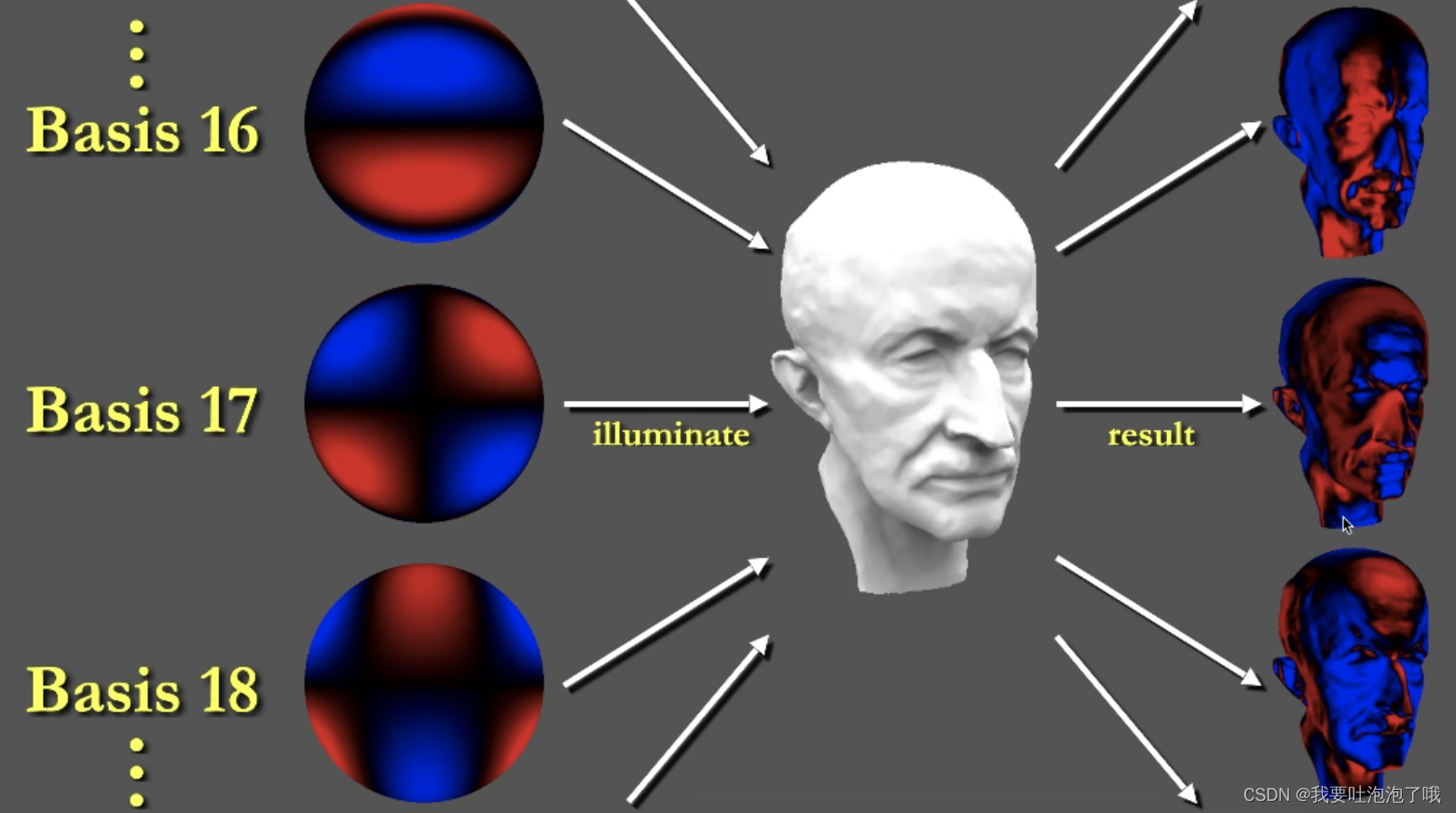
5.1.2 计算方法2
直接按照lighting和light transport的prt思路,在渲染方程 L ( o ) = ∫ Ω L ( i ) ⋅ T ( i , o ) d i L(o) = \int_{Ω}L(i) \cdot T(i,o)di L(o)=∫ΩL(i)⋅T(i,o)di里带入以下(1)(2)式,将lighting和light transport分别使用SH描述:
L ( ω i ) ≈ ∑ p c p B p ( ω i ) —— ( 1 ) L(ω_i) ≈ \sum_{p} c_pB_p(ω_i)——(1) L(ωi)≈p∑cpBp(ωi)——(1) T ( ω i ) ≈ ∑ q c q B q ( ω i ) —— ( 2 ) T(ω_i) ≈ \sum_{q} c_qB_q(ω_i)——(2) T(ωi)≈q∑cqBq(ωi)——(2) L o ( p , ω o ) = ∫ Ω L i ( p , ω i ) f r ( p , ω i , ω o ) c o s θ i V ( p , ω i ) d ω i = ∑ p ∑ q c p c q ∫ Ω + B p ( ω i ) B q ( ω i ) d ω i L_o(p,ω_o) = \int_{Ω}L_i(p,ω_i)f_r(p,ω_i,ω_o)cosθ_i V(p,ω_i) dω_i = \sum_{p}\sum_{q}c_pc_q\int_{Ω+}B_p(ω_i)B_q(ω_i)dω_i Lo(p,ωo)=∫ΩLi(p,ωi)fr(p,ωi,ωo)cosθiV(p,ωi)dωi=p∑q∑cpcq∫Ω+Bp(ωi)Bq(ωi)dωi
由SH的正交性,积分项只有0和1两种可能,并且只有在p=q的时候才有值,所以还是等于两个向量点乘,与方法1结果一致。
5.1.3 方法总结
- 两种方法都是通过用SH描述的预计算,将着色过程转化为两个向量的点乘,性能提升NN倍。对于可见性计算方式,可以从着色点向四周发射采样光线,并且是预计算(假设景物场景)。
- 不仅可以计算带阴影的环境光照,还可以在多次bounce的间接光场景下做预计算

- 在天空、日出等场景下也可以用预计算参与部分计算,UE4在skylight上的实现原理参考Disney原则的PBR在UE4中的应用这篇文章
- 闫老师认为prt在目前光追普及的情况下甚至会有更多表现空间,这两年会发展
5.2 glossy case
- glossy 场景下brdf就不是常数了,与入射光和出射光方向都有关系,由于参数空间不一致就不能将light transport项投影到lighting的这一个SH上了,而是一个关于一组出射方向o的SH函数: L ( o ) ≈ ρ ∑ l i T i → L ( o ) ≈ ∑ l i T i ( o ) L(o) ≈ ρ \sum l_i T_i →L(o) ≈ \sum l_i T_i(o) L(o)≈ρ∑liTi→L(o)≈∑liTi(o)
- 将 T i ( o ) T_i(o) Ti(o)投影到SH上 T i ( o ) ≈ ∑ t i j B j ( o ) T_i(o) ≈ \sum t_{ij}B_j(o) Ti(o)≈∑tijBj(o),其中 t i j t_{ij} tij是球谐矩阵,大小为:不同方向采样次数m*基函数个数n。
- 代入得到 L ( o ) ≈ ∑ l i ∑ t i j B j ( o ) = ∑ ( ∑ l i t i j ) B j ( o ) L(o) ≈ \sum l_i \sum t_{ij}B_j(o) = \sum (\sum l_it_{ij})B_j(o) L(o)≈∑li∑tijBj(o)=∑(∑litij)Bj(o),这样就从diffuse的两个向量点乘变成了glossy的向量与矩阵点乘。
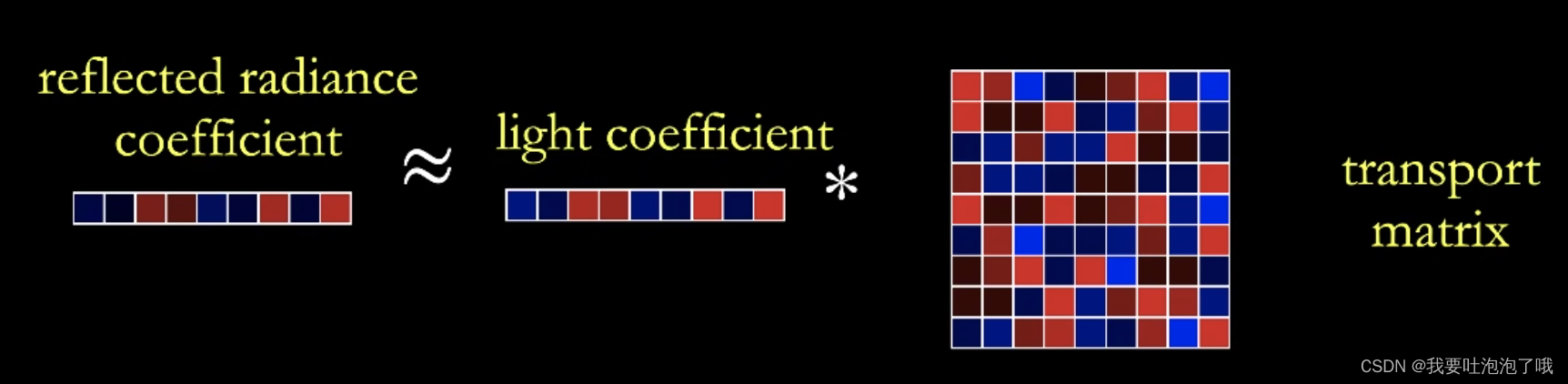
- 总结:
- diffuse一般用3阶就可以描述,glossy一般用4到5阶甚至更多(科研里10阶都嫌少-_-)
- glossy效率比diffuse低很多,存储空间也需要更大(每个点存矩阵25*25及更多),以目前的硬件水平4阶计算可以到100帧左右(电脑)

5.3 interreflection case(互反射)/multi bounce间接光
- 对于多次反射的间接光而言,不管光线从光源发出到我们眼睛之间经历了多少diffuse或specular或glossy(介于前两者之间)的物体,他都相当于PRT中的light transport项,过程再复杂都是可以预计算的。(light transport复杂度与渲染效率无关)
5.4 总结
- PRT就是用SH来描述lighting和light transport两部分,并且将light transport项实现预计算,diffuse相当于向量点乘,glossy相当于向量和矩阵点乘的计算量,算得飞快;并且还能描述多bounce反射光和环境光阴影等场景。
- PRT也有问题,它只适合描述低频,因为对于高频部分的细节非常高阶效果也一般,见下图;另外它还要求场景不能移动、物体材质不能改变,整个场景是静态的(假设可见性不变)。

- tips:
- PRT关注的更多的是已知brdf的预计算,spatially varying(空间变换)的 brdf可以用一些噪声辅助计算。
- 预计算部分是独立的,不在光栅化里。(raytracing在现在硬件里可以在光栅化里实现了)
5.5 拓展:其他基函数
研究应用中还有很多其他基函数,比如Wavelet小波函数、Zonal Harmonics、Spherical Gaussian球面高斯(SG)、Piecewise Constant等。这里老师介绍一下Wavelet小波函数:
二维Haar小波函数是定义在图像块上的基函数(不同于SH在球面上),如下图,三四列和行都有一半灰色也就是没有定义,黑白代表正负。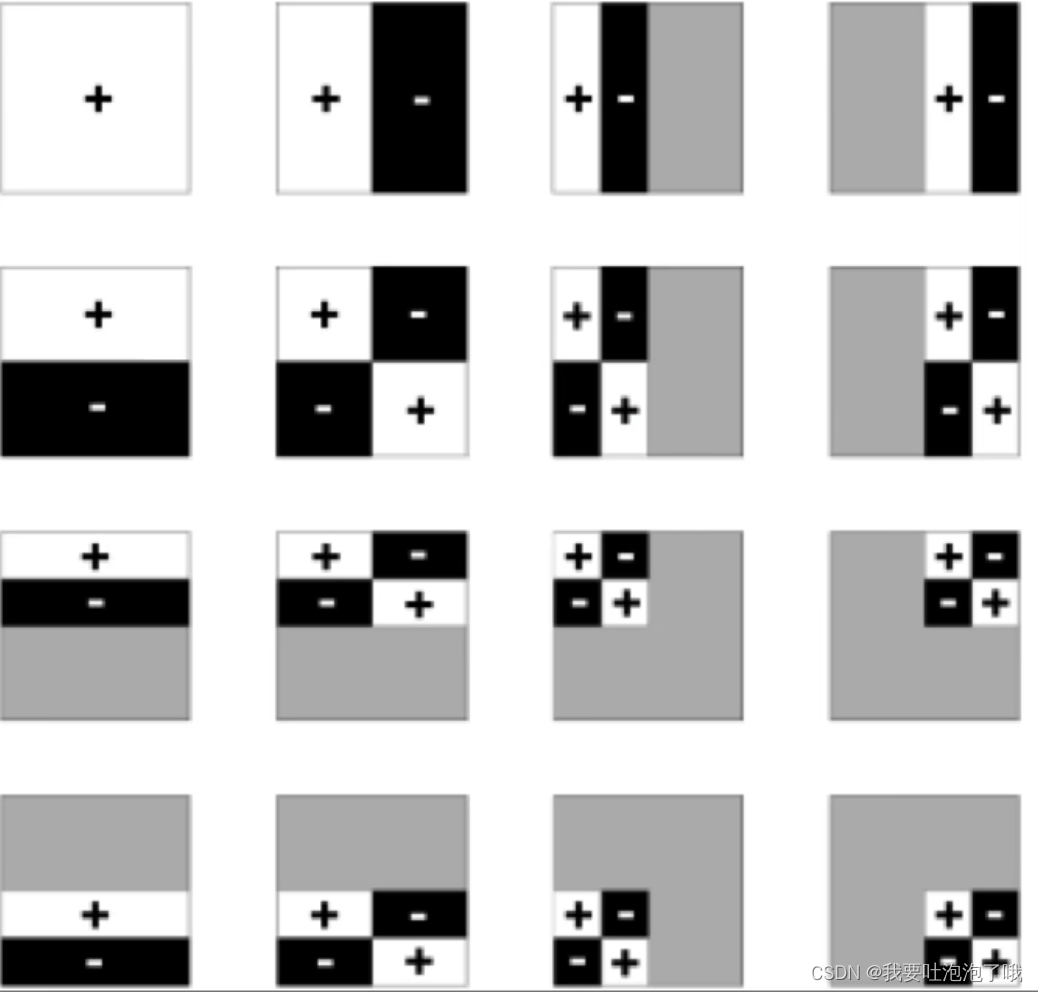
- SH可以通过取前n阶来描述,Haar小波函数由于投影完成后会有大量系数接近0,因此可以选择保留系数中最大的n个来压缩。特征:非线性全频率,低频高频都可以表示
- 因为二维描述球面可能会有接缝,所以一般会用cubemap记录光照。对每面纹理来说,小波函数把纹理分为4格把高频信息留在除右上右下左下三格中,然后对左上格重复迭代这个操作,如下图




- 可以看到最后图片大部分都是灰色,正说明有大量次要信息可以舍去,实现高效压缩。「jepg就是用类似小波变换的离散余弦变换来压缩图片的」下图展示了SH了小波函数对高频信息的描述效果,可以看到小波还原程度很高。
- 可是小波函数有个严重问题:不支持光照旋转,因此每次旋转光照都得重新进行预计算。

参考资料
边栏推荐
- Application scenarios of js anti-shake function and function throttling
- iNFTnews | 看见元宇宙的两面,何谓全真互联网和价值互联网?
- 瑞萨RZ/G2L处理器详细测评
- TimerTask(addin timer语音)
- MySql tens of millions of paging optimization, fast insertion method of tens of millions of data
- HikariCP数据库连接池,太快了!
- 用了TCP协议,就一定不会丢包嘛?
- LayaBox---TypeScript---Three slash instructions
- LayaBox---TypeScript---Iterator and generator
- qq邮箱日发5万邮件群发技术(qq邮箱怎样定时发送邮件)
猜你喜欢
随机推荐
牛客网项目17节生成验证码 刷新验证码一直没反应
LayaBox---TypeScript---JSX
STL中list实现
Naive Bayesian Method of Li Hang's "Statistical Learning Methods" Notes
QT专题:组合会话框和文本编辑器
Mistakes in Brushing the Questions 1-Implicit Conversion and Loss of Precision
3D激光slam:LeGO-LOAM---地面点提取方法及代码分析
LayaBox---TypeScript---Decorator
行为型模式-策略模式
阿里CTO程立:阿里巴巴开源的历程、理念和实践
Using the TCP protocol, will there be no packet loss?
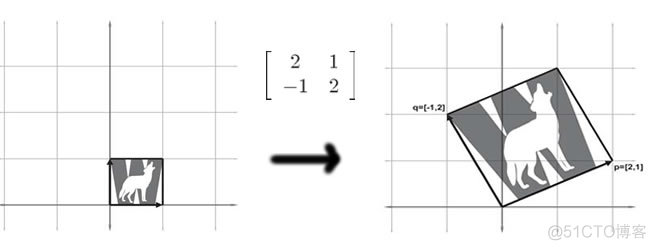
图形化矩阵,矩阵到底长什么样?
LayaBox---TypeScript---高级类型
斯皮尔曼相关系数
你认同这个观点吗?大多数企业的数字化都只是为了缓解焦虑
R语言使用ggpubr包的ggtexttable函数可视化表格数据(直接绘制表格图或者在图像中添加表格数据)、设置theme主题参数自定义表格中表头内容的填充色(使用colnames.style参数)
Verilog的随机数系统任务----$random
LayaBox---TypeScript---三斜线指令
适配器模式适配出栈和队列及优先级队列
你好,我的新名字叫“铜锁/Tongsuo”