The k-nearest neighbor method in the notes of Li Hang's "Statistical Learning Methods"

第三章 k近邻法

1.Samples with the same label usually have many similar features,So the same category may get together phenomenon,也就是物以类聚.

2.Every sample comes in,We look at what class the samples around it are,Then it is also very likely to fall into this category.

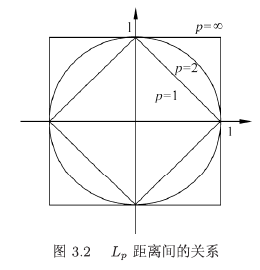
距离度量Distance measure

首先令 $ x_{i}=\left(x_{i}^{(1)}, x_{i}^{(2)}, \ldots, x_{i}^{(n)}\right), x_{j}=\left(x_{j}^{(1)}, x_{j}^{(2)}, \ldots, x_{j}^{(n)}\right) $

欧式距离（Also called two-norm）：

$L_2\left(x_i,x_j\right)={\left({\sum }_{i=1}^n{\left|x_i^{(l)}-x_j^{(l)}\right|}^2\right)}^{\frac{1}{2}}$

曼哈顿距离（Also called a norm）：

$L_1\left(x_i,x_j\right)={\sum }_{i=1}^n\left|x_i^{(l)}-x_j^{(l)}\right|$

P范数:

$L_{\mathrm{p}}\left(x_i,x_j\right)={\left({\sum }_{l=1}^n{\left|x_i^{(l)}-x_j^{(l)}\right|}^p\right)}^{\frac{1}{p}}$

切比雪夫距离（Similar to the queen of chess）

当 $p=\infty$ 时, 它是各个坐标距离的最大值, 即

$L_{\infty }\left(x_i,x_j\right)={\max }_l\left|x_i^{(l)}-x_j^{(l)}\right|$

k值的选择

k值的选择会对k近邻法的结果产生重大影响.
如果选择较小的k值,就相当于用较小的邻域中的训练实例进行预测,“学习”的近似误差(approximation error)会减小,只有与输入实例较近的(相似的)训练实例才会对预测结果起作用.但缺点是“学习”的估计误差(estimation error)会增大,预测结果会对近邻的实例点非常敏感.如果邻近的实例点恰巧是噪声,预测就会出错.换句话说,k值的减小就意味着整体模型变得复杂,容易发生过拟合.

如果选择较大的k值,就相当于用较大邻域中的训练实例进行预测.其优点是可以减少学习的估计误差,但缺点是学习的近似误差会增大.这时与输入实例较远的(不相似的)训练实例也会对预测起作用,使预测发生错误.k值的增大就意味着整体的模型变得简单.

如果k =N,那么无论输入实例是什么,都将简单地预测它属于在训练实例中最多的类.这时,模型过于简单,完全忽略训练实例中的大量有用信息,是不可取的.

在应用中,k值一般取一个比较小的数值.通常采用交叉验证法来选取最优的k值.

分类决策规则

k近邻法中的分类决策规则往往是多数表决,即由输入实例的k个邻近的训练实例中的多数类决定输入实例的类.

多数表决规则(majority voting rule)有如下解释:如果分类的损失函数为0-1损失函数．分类函数为：

$f:{\mathbf{R}}^n\to \left\{c_1,c_2,\cdots ,c_K\right\}$

那么误分类的概率是

$P(Y\ne f(X))=1-P(Y=f(X))$

对给定的实例 $x \in \mathcal{X} $, 其最近邻的 k 个训练实例点构成集合 $ N_{k}(x) $ .如果涵盖 $N_{k}(x) $ 的区域的类别是 $c_j$ , 那么误分类率是

$\frac{1}{k}{\sum }_{x_i\in N_k(x)}I\left(y_i\ne c_j\right)=1-\frac{1}{k}{\sum }_{x_i\in N_k(x)}I\left(y_i=c_j\right)$

要使误分类率最小即经验风险最小, 就要使 $ \sum_{x_{i} \in N_{k}(x)} I\left(y_{i}=c_{j}\right) $ 最大, 所以多数表决规则等价于经验风险最小化.

注意：$I\left(x\right)$为指示函数,即x条件为真,则函数值为1,x条件为假,则函数值为0.

总结Summarization

1. K近邻思想:物以类聚

2. K近邻没有显式的训练过程（A distance metric is calculated between the new sample and the original sample）

3. 距离度量:
   (1)欧式距离:A straight line between two points

   (2)曼哈顿距离:City block distance

   (3)切比雪夫距离:棋盘距离

4. 分类决策规则:多数表决