当前位置:网站首页>CFdiv2-The Number of Imposters-(两种点集图上染色问题总结)
CFdiv2-The Number of Imposters-(两种点集图上染色问题总结)
2022-08-02 09:05:00 【可爱美少女】
题意:
就是给你n个人,和m句话。每句话是a说b是好人或者坏人。问你这些人中最多有多少坏人。当然如果这m句话有错误出现驳论那么就输出-1。
思考:
1.这是很久之前做的题了。有两种做法,种类并查集和两种点集图上染色。这里就整理第二种做法。首先,这些人可以很明显的去合并和分类,意思就是,a说b是好人,那么a和b就在一类,如果不是好人,那么就不在一类。
2.那么可以对a和b建边,权值为1的时候代表a和b是一类,权值为0的时候代表a和b不是一类。建立完边后呢?那么一个连通块的人,只要确定了一个人的身份,剩下的身份就全部出来了。那么这里面颜色为1的和为2的,就可以随意转化,为1的可以是好人也可以是坏人。
3.那么既然有可能出现驳论,那么怎么判断呢?如果a说b是好人,那么a和b肯定是同一颜色的,因为他俩是一个帮派,无论是好人帮派还是坏人帮派。如果a搜到b的时候,发现b此时已经有颜色了,并且还和自己的颜色不一样,那么就出现驳论了。同理a说是b是坏人,但是a和b的颜色一样了,那么也是错误的。然后怎么求最多的坏人呢?因为一个连通块里面,颜色1和2可以随意转化,那么就让颜色多的是坏人即可。
代码:
#include<bits/stdc++.h>
#define fi first
#define se second
#define pb push_back
#define db double
#define int long long
#define PII pair<int,int >
#define mem(a,b) memset(a,b,sizeof(a))
#define IOS std::ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
using namespace std;
const int mod = 1e9+7,inf = 1e18;
const int N = 2e5+10,M = 2010;
int T,n,m,k;
int va[N];
int col[N];
int cnt[2];
int suc = 1;
vector<PII > e[N];
void dfs(int now)
{
cnt[col[now]]++;
for(auto t:e[now])
{
int spot = t.fi,w = t.se;
if(!col[spot])
{
if(w==1) col[spot] = 3-col[now];
else col[spot] = col[now];
dfs(spot);
}
else
{
if(w==1&&col[spot]==col[now]) suc = 0;
if(w==0&&col[spot]!=col[now]) suc = 0;
}
}
}
signed main()
{
IOS;
cin>>T;
while(T--)
{
cin>>n>>m;
for(int i=1;i<=n;i++)
{
col[i] = 0;
e[i].clear();
}
while(m--)
{
int a,b;string s;
cin>>a>>b>>s;
if(s=="imposter")
{
e[a].pb({
b,1});
e[b].pb({
a,1});
}
else
{
e[a].pb({
b,0});
e[b].pb({
a,0});
}
}
suc = 1;
int ans = 0;
for(int i=1;i<=n;i++)
{
if(!col[i])
{
col[i] = 1;
cnt[1] = cnt[2] = 0;
dfs(i);
ans += max(cnt[1],cnt[2]);
}
}
if(suc) cout<<ans<<"\n";
else cout<<-1<<"\n";
}
return 0;
}
题意:
就是给你n个门,有的是打开的状态有的是关闭的状态,然后给你m个开关,每个开关控制一些门。按下开关,可以让他控制的所有的门变成相反的状态。然后每个门就有两个开关控制它。现在问你是否可以按下某些开关,让这些门全部变成打开或者关闭的状态。
思考:
1.当时看到这题,对于开着的门,它的两个开关要么都按要么都不按,对于关着的门,他的两个开关只能按其中一个。那么我就想了并查集,如果开着的,那么两个开关必须在一个集合。然后再对关着的门看看他的两个开关是否在一个集合里面,如果在那么代表这两个开关必须同时选,所以就不满足自己了,但是发现错了。因为还有别的可能,然后推了推我发现这是个类似二分图的东西,有好几个连通块去处理啥的。注意这里不是二分图,自己的理解有误。到这里就感觉卡死做不下去了。
2.然后看了下提示,说是把门当边,两个开关当点,建图。看到这,我就想到了以前做的说谎者。如果门是开着的,那么a开关和b开关是肯定在一个集合里面的,所以a和b连一条为1的边。如果关着的就连为0的边。
3.我都想到这里了,但是不知道脑子里想的什么,总感觉这该怎么去颜色呢?因为对于一个连通块,你不能随便去颜色,会对别的连通块有影响。其实这里不同的连通块肯定是没啥影响的呀,都没有交集。这里我认为有影响是因为我第一个做法写的时候,不同的连通块之间是有·影响的,所以就…。
4.那么此时缓过来,就可以发现对图颜色就行了,如果没有驳论的话那么就可以让整个图都满足我建立的边的条件,那么就可以让所有的门都是开着的。
5.还有个值得注意的点就是,判断是否颜色出现错误的时候,要在dfs里面跑的时候就判断。如果你出来再判断,一些没边的点也会颜色,可能就会对答案有影响(可能,这个还是看你写题的姿势)。
代码:
#include<bits/stdc++.h>
#define fi first
#define se second
#define pb push_back
#define db double
#define int long long
#define PII pair<int,int >
#define mem(a,b) memset(a,b,sizeof(a))
#define IOS std::ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
using namespace std;
const int mod = 1e9+7,inf = 1e18;
const int N = 2e5+10,M = 2010;
int T,n,m,k;
int va[N];
int col[N];
int suc = 1;
vector<int > v[N];
vector<PII > e[N];
void dfs(int now)
{
for(auto t:e[now])
{
int spot = t.fi,w = t.se;
if(!col[spot])
{
if(w==1) col[spot] = col[now];
else col[spot] = 3-col[now];
dfs(spot);
}
else
{
if(w==1&&col[spot]!=col[now]) suc = 0;
if(w==0&&col[spot]==col[now]) suc = 0;
}
}
}
signed main()
{
IOS;
cin>>n>>m;
for(int i=1;i<=n;i++) cin>>va[i];
for(int i=1;i<=m;i++)
{
cin>>k;
while(k--)
{
int x;
cin>>x;
v[x].pb(i);
}
}
for(int i=1;i<=n;i++)
{
int a = v[i][0],b = v[i][1];
e[a].pb({
b,va[i]});
e[b].pb({
a,va[i]});
}
for(int i=1;i<=m;i++)
{
if(!col[i]) col[i] = 1,dfs(i);
}
suc?cout<<"YES\n":cout<<"NO\n";
return 0;
}
题意:
就是给你n个点和m条边,每条边有一个颜色黑或者白。然后你可以在一个点进行操作,可以使得这个点的所有边的颜色都反转。问你是否可以通过操作,使得所有边的颜色都一样,如果可以输出最小的操作次数,和操作的点。如果不可以就输出-1。
思考:
代码:
#include<bits/stdc++.h>
#define fi first
#define se second
#define pb push_back
#define db double
#define int long long
#define PII pair<int,int >
#define mem(a,b) memset(a,b,sizeof(a))
#define IOS std::ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
using namespace std;
const int mod = 1e9+7,inf = 1e18;
const int N = 2e5+10,M = 2010;
struct node{
int a,b,c;
};
int T,n,m,k;
node va[N];
int col[N];
int cnt[3];
int suc = 1;
int minn = inf;
vector<int > v1,v2;
vector<int > anw;
vector<PII > e[N];
void dfs(int now)
{
if(col[now]==1) v1.pb(now);
else v2.pb(now);
cnt[col[now]]++;
for(auto t:e[now])
{
int spot = t.fi,w = t.se;
if(!col[spot])
{
if(w==1) col[spot] = col[now];
else col[spot] = 3-col[now];
dfs(spot);
}
else
{
if(w==1&&col[spot]!=col[now]) suc = 0;
if(w==0&&col[spot]==col[now]) suc = 0;
}
}
}
void solve(int op)
{
suc = 1;int ans = 0;
for(int i=1;i<=n;i++)
{
col[i] = 0;
e[i].clear();
}
for(int i=1;i<=m;i++)
{
int a = va[i].a,b = va[i].b,c = va[i].c;
if(op) c ^= 1;
e[a].pb({
b,c});
e[b].pb({
a,c});
}
vector<int > v;
for(int i=1;i<=n;i++)
{
if(!col[i])
{
col[i] = 1;
cnt[1] = cnt[2] = 0;
v1.clear();v2.clear();
dfs(i);
ans += min(cnt[1],cnt[2]);
if(cnt[1]<cnt[2]) for(auto t:v1) v.pb(t);
else for(auto t:v2) v.pb(t);
}
}
if(suc&&minn>ans)
{
minn = ans;
anw = v;
}
}
signed main()
{
IOS;
cin>>n>>m;
for(int i=1;i<=m;i++)
{
int a,b;char op;
cin>>a>>b>>op;
if(op=='B') va[i] = {
a,b,1};
else va[i] = {
a,b,0};
}
solve(0);solve(1);
if(minn==inf) cout<<-1<<"\n";
else
{
cout<<minn<<"\n";
for(auto t:anw) cout<<t<<" ";
}
return 0;
}
题意:
思考:
刚开始还想,每次加一条边,染色一次,但是同一个连通块的点必须一次染完,不能分开染色再去合并。
代码:
#include<bits/stdc++.h>
#define fi first
#define se second
#define pb push_back
#define db double
#define int long long
#define PII pair<int,int >
#define mem(a,b) memset(a,b,sizeof(a))
#define IOS std::ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
using namespace std;
const int mod = 1e9+7,inf = 1e18;
const int N = 2e5+10,M = 2010;
struct node{
int a,b,c;
};
int T,n,m,k;
node va[N];
int suc = 1;
vector<int > v;
map<int,int > col;
vector<PII > e[N];
int get(int x)
{
return lower_bound(v.begin(),v.end(),x)-v.begin()+1;
}
void dfs(int now)
{
for(auto t:e[now])
{
int spot = t.fi,w = t.se;
if(!col[spot])
{
if(w==1) col[spot] = col[now];
else col[spot] = 3-col[now];
dfs(spot);
}
else
{
if(w==1&&col[spot]!=col[now]) suc = 0;
if(w==0&&col[spot]==col[now]) suc = 0;
}
}
}
bool check(int mid)
{
suc = 1;col.clear();
for(int i=0;i<=2*m+10;i++) e[i].clear();
for(int i=1;i<=mid;i++)
{
int a = va[i].a,b = va[i].b,c = va[i].c;
e[a].pb({
b,c});
e[b].pb({
a,c});
}
for(int i=1;i<=mid;i++)
{
int a = va[i].a;
if(!col[a])
{
col[a] = 1;
dfs(a);
}
}
return suc;
}
signed main()
{
IOS;
cin>>n>>m;
for(int i=1;i<=m;i++)
{
int a,b;string s;
cin>>a>>b>>s;
if(s=="even") va[i] = {
a-1,b,1};
else va[i] = {
a-1,b,0};
v.pb(a-1);v.pb(b);
}
sort(v.begin(),v.end());
v.erase(unique(v.begin(),v.end()),v.end());
for(int i=1;i<=m;i++)
{
va[i].a = get(va[i].a);
va[i].b = get(va[i].b);
}
int l = 0,r = m;
while(l<r)
{
int mid = (l+r+1)>>1;
if(check(mid)) l = mid;
else r = mid-1;
}
cout<<l;
return 0;
}
边栏推荐
- 膜拜,Alibaba分布式系统开发与核心原理解析手册
- nacos项目搭建
- Bigder:41/100生产bug有哪些分类
- shell脚本
- Overview of Edge Computing Open Source Projects
- 文章解读 -- FlowNet3D:Learning Scene Flow in 3D Point Clouds
- 你有了解过这些架构设计,架构知识体系吗?(架构书籍推荐)
- Detailed explanation of calculation commands in shell (expr, (()), $[], let, bc )
- Fiddler(七) - Composer(组合器)克隆或者修改请求
- pnpm的安装与使用
猜你喜欢
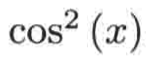
普林斯顿微积分读本03第二章--编程实现函数图像绘制、三角学回顾
Redisson实现分布式锁
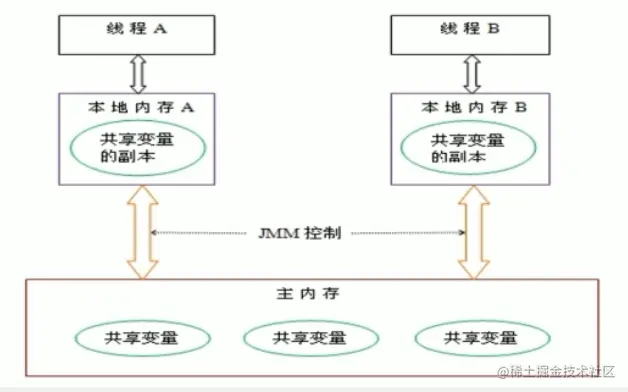
谈谈对Volatile的理解

裁员趋势下的大厂面试:“字节跳动”

Daily practice of dynamic programming (3)

破解wifi密码 暴力破解 保姆式教学
膜拜,Alibaba分布式系统开发与核心原理解析手册
![[Must read] Mylander valuation analysis, electrical stimulation products for pelvic and postpartum rehabilitation](/img/25/e16bac4e789cddadffd43ed9e9df7c.jpg)
[Must read] Mylander valuation analysis, electrical stimulation products for pelvic and postpartum rehabilitation

Spend 2 hours a day to make up for Tencent T8, play 688 pages of SSM framework and Redis, and successfully land on Meituan

在 QT Creator 上配置 opencv 环境的一些认识和注意点
随机推荐
恋爱十不要
2022牛客暑期多校训练营4(ADHKLMN)
Redis数据结构
利用minlm比较句子之间的相似度
Redisson报异常attempt to unlock lock, not locked by current thread by node id解决方案
Postman download localization of installation and use
了解下C# 多线程
UVM信息服务机制
nacos项目搭建
百数应用中心——选择一款适合企业的标准应用
Fiddler(七) - Composer(组合器)克隆或者修改请求
【微信小程序2】事件绑定
Gorilla Mux 和 GORM 的使用方法
新起点丨MeterSphere开源持续测试平台v2.0发布
破解wifi密码 暴力破解 保姆式教学
【并发编程】- 线程池使用DiscardOldestPolicy策略、DiscardPolicy策略
PyCharm使用教程(详细版 - 图文结合)
【微信小程序】本地服务页面案例实现
pnpm: Introduction
Pycharm (1) the basic use of tutorial