(hdu1588) Gauss Fibonacci (sum of matrix fast power + bisection matrix proportional sequence)

Topic link ：Problem - 1588

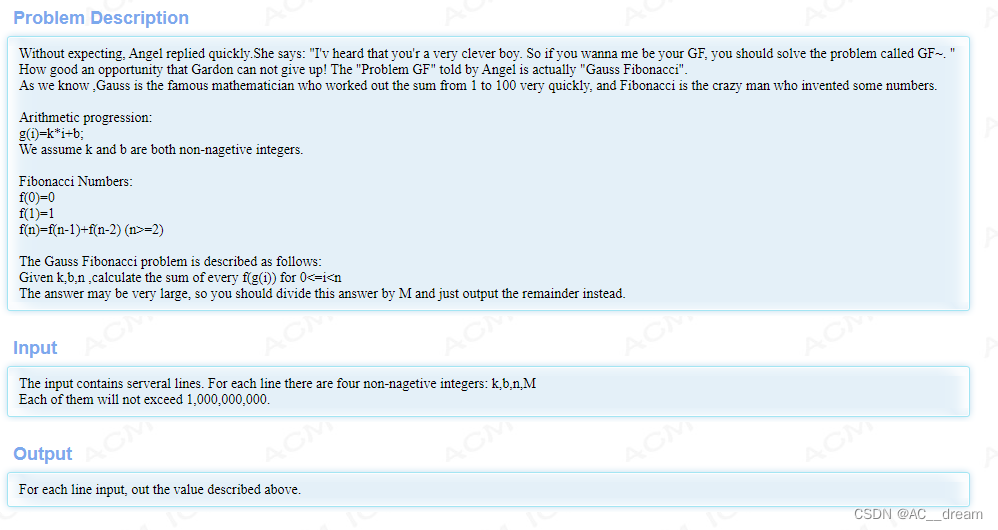
The sample input ：

2 1 4 100
2 0 4 100

Sample output ：

21
12

The question ： Have function g(i)=k*i+b,f(i) It's Fibonacci number i Item value , Among them is ：

f(0)=0

f(1)=1

f(n)=f(n-1)+f(n-2)

Multiple tests , Each set of tests is given four numbers k,b,n,m, seek

By matrix fast power O（logn） Solving Fibonacci series, we can know ,f(i)=M^(i-1) The first element value of , Where the matrix M It's a 2*2 Matrix {1,1,1,0} For arbitrary i Yes g(i)=k*i+b, that f(g(i))=M^(k*i+b-1) The first element value of , Then there is ：（ Following M Refers to its first element value ）

  as for M^(b-1) and M^k Are relatively easy to find , Hypothetical hypothesis B=M^k, Then the problem turns into how to find , The sum of this matrix can be solved by dichotomy , The problem process can be simulated as follows ：

In order to B^0+B^1+……+B^9 For example ：

utilize ANS The matrix records the final answer ,ans The matrix records the left coefficient ,E Is the unit matrix

B^0+B^1+B^2+B^3+B^4+B^5+B^6+B^7+B^8+B^9=B^0+B^9+(E+B^4)*(B^1+B^2+B^3+B^4)

=B^0+B^9+(E+B^4)*(E+B^2)*(B^1+B^2)=B^0+B^9+(E+B^4)*(E+B^2)*(E+B^1)*(B^1)

among ANS What is recorded is in the process B^0+B^9 Equal odd degree term , and ans The record is (E+B^4)*(E+B^2)*(E+B^1) And so on , It is easy to find that this process is O(logn) Of , So you can pass this question within the specified time .

The last thing to explain is ： Seeing the formula, we found that we need to ask M^(b-1), When b by 0 When we directly order b=k,n-- that will do , The principle is 0+0,k+0,2*k+0,……,n*k+0 Equivalent to 0+k,k+k,2*k+k,……,(n-1)*k+k, There is one less item in the back than in the front , At that time 0 Items for 0, So it doesn't matter , Just pay attention to this place

See the code for the specific process ：

#include<iostream>
#include<algorithm>
#include<cstring>
#include<cstdio>
#include<cmath>
#include<vector>
#include<queue>
using namespace std;
typedef long long ll;
ll ANS[3][3],ans[3][3],f[3][3],E[3][3];
ll k,b,n,mod;
void mul(ll a[3][3],ll b[3][3],int op)//a=a*b||b=a*b
{
	ll t[3][3]={0};
	for(int i=1;i<=2;i++)
	for(int j=1;j<=2;j++)
	for(int k=1;k<=2;k++)
		t[i][k]=(t[i][k]+a[i][j]*b[j][k])%mod;
	if(op==1)
	{
		for(int i=1;i<=2;i++)
		for(int j=1;j<=2;j++)
			a[i][j]=t[i][j];
	}
	else 
	{
		for(int i=1;i<=2;i++)
		for(int j=1;j<=2;j++)
			b[i][j]=t[i][j];
	}
}
void add(ll a[3][3],ll b[3][3])//a=a+b
{
	for(int i=1;i<=2;i++)
	for(int j=1;j<=2;j++)
		a[i][j]=(a[i][j]+b[i][j])%mod;
}
void qpow(ll a[3][3],ll n,ll b[3][3])//b=a^n
{
	ll tans[3][3]={0};
	tans[1][1]=tans[2][2]=1;
	ll t[3][3]={0};
	for(int i=1;i<=2;i++)
	for(int j=1;j<=2;j++)
		t[i][j]=a[i][j];
	while(n)
	{
		if(n&1)	 mul(tans,t,1);
		mul(t,t,1);
		n>>=1;
	}
	for(int i=1;i<=2;i++)
	for(int j=1;j<=2;j++)
		b[i][j]=tans[i][j];
}
void qmul(ll f[3][3],ll n)// seek f^0+f^1+……+f^n 
{
	ANS[1][1]=ANS[2][2]=1;
	ans[1][1]=ans[2][2]=1;
	ll t[3][3]={0};
	while(n)
	{
		if(n&1)
		{
			qpow(f,n,t);
			mul(ans,t,2);
			add(ANS,t);
		}
		n>>=1;
		qpow(f,n,t);
		E[1][1]=E[2][2]=1;
		E[1][2]=E[2][1]=0;
		add(E,t);
		mul(ans,E,1);
	}
}
int main()
{
	while(scanf("%lld%lld%lld%lld",&k,&b,&n,&mod)!=EOF)
	{
		if(b==0) b=k,n--;
		memset(ANS,0,sizeof ANS);
		memset(ans,0,sizeof ans);
		f[1][1]=f[1][2]=f[2][1]=1;f[2][2]=0;
		ll t[3][3]={0};
		qpow(f,k,t);
		qmul(t,n-1);
		qpow(f,b-1,t);
		mul(t,ANS,1);
		printf("%lld\n",t[1][1]);
	}
	return 0;
}