Eigen矩阵运算库快速上手

目录

1. 配置

2. 初始化

2.1 Array类

2.2 Vector类

2.3 Matrix类

2.4 Vector赋值

2.5 高级初始化

3. 矩阵计算

3.1 矩阵基本计算

3.2 线性求解

3.3 特征值计算

3.4 奇异值分解

总结

做科研类项目，尤其是与线性优化，主成分分析有关的项目，势必需要用到矩阵计算及相关的优化工具。很多同学会利用matlab完成项目需求，这当然是一个不错的选择。但是，对于平台有一定要求的项目，尤其是那些基于C++开发的工程项目，使用matlab就会带来一些不便。我们希望有方便的矩阵开源工具，可以集成在项目中，以简化程序部署与使用的难度。这里就不得不提到大名鼎鼎的矩阵开源库，Eigen。今天这篇博客，就来跟大家介绍下Eigen部署与使用的基本知识，方便新手朋友能够快速掌握基于Eigen实现的矩阵计算与优化功能。

---

1. 配置

首先我们在官网上下载Eigen最新版本(V3.4)

3.4.0 · libeigen / eigen · GitLab

这里我们使用VS2022作为开发平台。配置非常简单，只要在VC++目录的include添加Eigen路径就可以。

 这里贴一段测试代码：

#include <iostream>
#include <Eigen/Dense>
using namespace Eigen;
using namespace std;
typedef Eigen::Matrix<int, 3, 3> Matrix3i;

int main()
{	
    Matrix3i m1;
    m1 << 1, 2, 3, 4, 5, 6, 7, 8, 9;
    cout << "m1 = \n" << m1 << endl;
    Matrix3i m2;
    m2 << 2, 0, 0, 0, 2, 0, 0, 0, 2;
    cout << "m2 = \n" << m2 << endl;
    cout << "m1 * m2 = \n" << (m1 * m2) << endl;
    return 0;
}

打印结果：

---

2. 初始化

在配置完Eigen后，接下来我们希望知道如何对向量和矩阵实现初始化。Eigen支持初始化方式很多， 参考博客Eigen库的使用小结，Eigen库的使用，Eigen初始化，我们列出几种供参考：

2.1 Array类

直接赋值

Eigen::Array<int, 3, 1> arr_1(1, 2, 3);

流输入赋值

Eigen::Array<int, 3, 3> arr_2;
    arr_2 <<
        1, 2, 3,
        4, 5, 6,
        7, 8, 9;

指针方式赋值

std::vector<int> vec_int{ 1,2,3,4,5,6,7,8,9 };
    Eigen::Array<int, 3, 3> arr_3(vec_int.data());

2.2 Vector类

Vector的赋值方法与Array基本相同。Vector可以被看做是一种特殊的Matrix。

Eigen::Vector3f v1 = Eigen::Vector3f::Zero();

Eigen::Vector3d v2(1.0, 2.0, 3.0);

Eigen::VectorXf v3(20); //维度为20的向量,未初始化.
v3 << 1.0 , 2.0 , 3.0;

2.3 Matrix类

与Array的初始化方法基本相同

Eigen::Matrix<double,2,2> m;
m << 1,2,3,4;

Eigen::MatrixXf m1(2,3);
m1 << 1,2,3,
	  4,5,6;

Eigen::Matrix3d m2 = Eigen::Matrix3d::Identity();//Eigen::Matrix3d::Zero();

Eigen::Matrix3d m3 = Eigen::Matrix3d::Random(); //随机初始化

2.4 Vector赋值

有的时候，我们会将数据存储在C++的数据结构vector中。此时，我们希望将vector的数据转换为矩阵，并进行相应计算。除了使用指针方式，我们还可以直接将vector的数据拷贝到矩阵中。

std::vector<std::vector<double>> LX;
MatrixXd m_Lx(LX.size(), 3);	
for (int i = 0; i < LX.size(); i++) {
	m_Lx(i, 0) = LX[i][0];
	m_Lx(i, 1) = LX[i][1];
	m_Lx(i, 2) = LX[i][2];
}

假设LX是一个点云数据，每一个点是一个三维向量。对应建立的MatrixXd m_LX即与LX具有相同的维度，即将C++的vector转换为eigen的matrix。

2.5 高级初始化

参考matlab，eigen也提供了一些功能丰富的高级数据初始化方法，包括对行列向量的独立赋值，块赋值等。这里我们列出一些示例代码，供参考。

列向量赋值

RowVectorXd rv1(1,2,3);

块赋值

对m4进行计算，并按块赋值给m5，输出m5： 

MatrixXf m4(2,2);
m4 << 1,2,3,4;
MatrixXf m5(4,4);
m5 << m4, m4 / 10, m4 * 10, m4;//将m5分了四块赋值

更加精准的赋值，首先输入第一行: 1, 2, 3; 之后按照block的信息，在矩阵的第二行，第一列插入一个2*2的子矩阵，4, 5, 6, 7；最后，在第三列，最后两个位置tail(2), 插入6, 9。可以看到，上述操作实现了对一个矩阵分块精准赋值。

Matrix3f m;
m.row(0) << 1,2,3;
m.block(1,0,2,2) << 4,5,6,7; 
m.col(2).tail(2) << 6,9;

---

3. 矩阵计算

基于赋值后的矩阵，我们希望通过Eigen实现对矩阵的计算。这里我们将矩阵计算分为三部分，包括矩阵基本计算，线性求解，特征值计算以及奇异值分解。

3.1 矩阵基本计算

矩阵基本计算比较简单，包括加，减，叉乘，点乘，转置，求逆等。

MatrixXf m = MatrixXf::Random(3,3);
MatrixXf m2 = MatrixXf::Random(3,3);
m.row(i);//矩阵第i行
m.col(j);//矩阵第j列
m.transpose();//转置
m.conjugate();//共轭
m.adjoint(); //共轭转置
m.minCoeff();//所有元素中最小元素
m.maxCoeff();//所有元素中最大元素
m.trace();//迹，对角元素的和
m.sum(); //所有元素求和
m.prod(); //所有元素求积
m.mean(); //所有元素求平均
m.dot(m2); //点乘
m.cross(m2);//叉乘

3.2 线性求解

求解Ax=b，eigen提供了几个工具，包括：

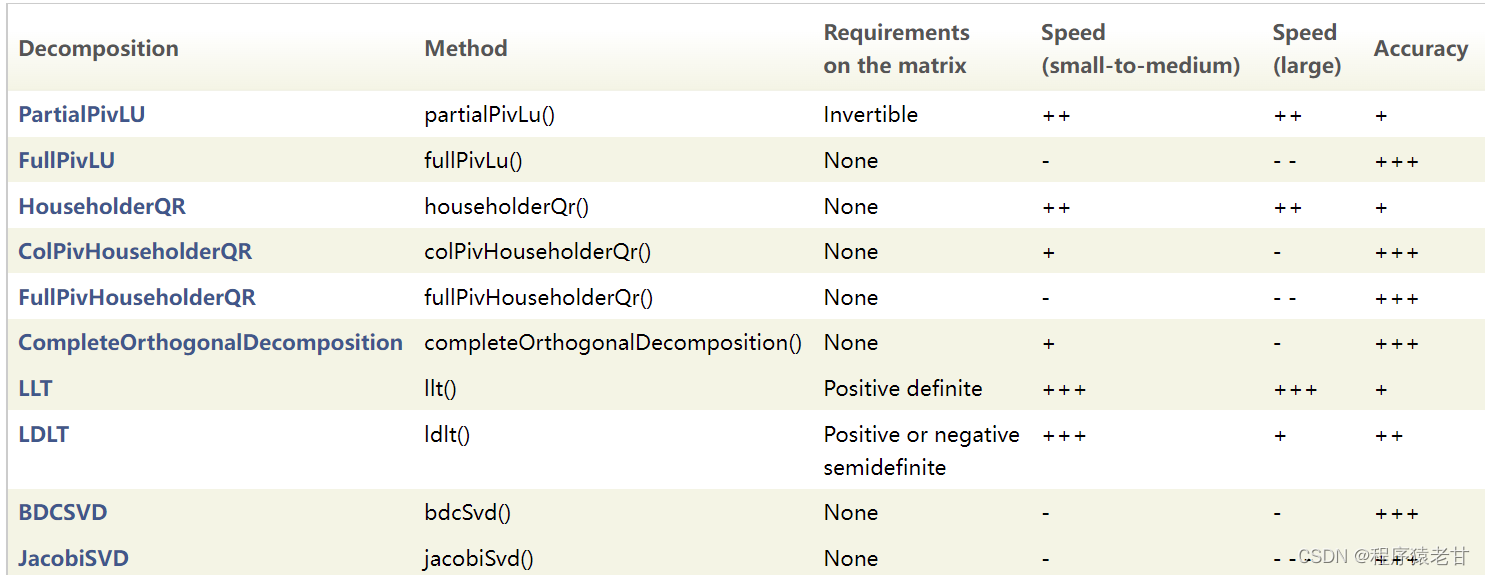
 一般大家会选择LLT和LDLT

 Eigen::Matrix2f A, b;
 A << 2, -1, -1, 3;
 b << 1, 2, 3, 1;
 std::cout << "Here is the matrix A:\n" << A << std::endl;
 std::cout << "Here is the right hand side b:\n" << b << std::endl;
 Eigen::Matrix2f x = A.ldlt().solve(b);//or A.llt().solve(B);                   
 std::cout << "The solution is:\n" << x << std::endl;

3.3 特征值计算

特征值及对应的特征向量计算，在矩阵分析中占有重要位置。基于Eigen的特征值计算如下：

Eigen::MatrixXd m = Eigen::MatrixXd::Random(3,3);
Eigen::MatrixXd mTm = m.transpose() * m;//构成中心对其的协方差矩阵

//计算
Eigen::SelfAdjointEigenSolver<Eigen::MatrixXd> eigen_solver(mTm);

//取出特征值和特征向量
Eigen::VectorXd eigenvalues = eigen_solver.eigenvalues();
Eigen::MatrixXd eigenvectors = eigen_solver.eigenvectors();

Eigen::VectorXd v0 = eigenvectors.col(0);// 因为特征值一般按从小到大排列,所以col(0)就是最小特征值对应的特征向量

3.4 奇异值分解

参考博客：矩阵奇异值分解简介

奇异值分解(singular value decomposition, SVD)：将矩阵分解为奇异向量(singular vector)和奇异值(singular value)。通过奇异值分解，我们会得到一些与特征分解相同类型的信息。然而，奇异值分解有更广泛的应用。每个实数矩阵都有一个奇异值分解，但不一定都有特征分解。例如，非方阵的矩阵没有特征分解，这是我们只能使用奇异值分解。

将矩阵A分解成三个矩阵的乘积：A=UDV^T。

这些矩阵中的每一个经定义后都拥有特殊的结构。矩阵U和V都被定义为正交矩阵，而矩阵D被定义为对角矩阵。注意，矩阵D不一定是方阵。对角矩阵D对角线上的元素被称为矩阵A的奇异值(singular value)。矩阵U的列向量被称为左奇异向量(left singular vector)，矩阵V的列向量被称为右奇异向量(right singular vector)。A的左奇异向量是AA^T的特征向量。A的右奇异向量是A^TA的特征向量。A的非零奇异值是A^TA特征值的平方根，同时也是AA^T特征值的平方根。

JacobiSVD<MatrixXd> svd(J, ComputeThinU | ComputeThinV);
U = svd.matrixU();
V = svd.matrixV();
D_t = svd.singularValues();

---

总结

作为基于C++的矩阵运算库，Eigen部署简单，执行效率高，集成了功能丰富的矩阵运算函数。掌握Eigen，能够显著提高项目对矩阵优化问题的求解效率。