当前位置:网站首页>[论文分享] VideoFlow: A Flow-Based Generative Model for Video
[论文分享] VideoFlow: A Flow-Based Generative Model for Video
2022-08-02 17:57:00 【fa1c4】
VideoFlow: A Flow-Based Generative Model for Video [ICML 2019]
Manoj Kumar Google Brain
Mohammad Babaeizadeh University of Illinois at Urbana-Champaign
概述
原则上可以学习捕捉复杂的现实世界现象, 来构建未来事件序列的生成模型. 视频预测的一个核心挑战是,未来是高度不确定的, 一系列过去对事件的观察可以暗示许多可能的未来. 最近的一些关于概率模型的研究可以揭示不确定的未来, 但是依赖于极高代价的计算力如像素级自回归模型, 或者不对数据本身的 likelihood 进行优化. 据作者所知,本篇是第一个提出使用规范化流进行多帧视频预测的工作,这允许直接优化数据 likelihood,并产生高质量的随机预测. 论文描述了一种对潜在空间动力学(latent space dynamics)进行建模的方法,并证明基于流的生成模型为视频生成建模提供了一种可行且具有竞争力的方法。
一句话: 使用规范化流进行多帧视频预测, 允许直接优化数据 likelihood 并产生高质量随机预测
论文代码集成在TensorFlow库中
https://github.com/tensorflow/tensor2tensor/blob/master/tensor2tensor/models/video/next_frame_glow.py
导论
背景
论文主要是根据过去一小段视频内容预测并合成原始RGB视频帧.
对未来视频帧进行预测的早期工作集中在确定性预测模型上, 确定性模型的大部分研究集中在结构(architectural)更改上,例如预测高级结构(high-level structure); 合并像素变换(incorporating pixel transformations); 预测编码结构(predictive coding architectures) 等等方法.
有了能够成功模拟许多确定性环境的模型,下一个关键挑战是通过建立能够有效地对不确定的未来进行推理的模型来应对随机性环境。在这种情况下,确定性模型要么忽略潜在的未来,要么产生模糊的预测,即可能未来的叠加或平均. 这个问题有三种解决方法:
(1) 基于变分自编码的模型 (models based on variational auto-encoders): 不直接最大化对数 likelihood,因为他们依赖于优化下界
(2) 生成式对抗网络 (generative adversarial networks): 计算成本高
(3) 自回归模型 (autoregressive models): 生成过程计算成本高
贡献
(1) 主要贡献是一个实用的基于流的视频预测模型架构,称之为VideoFlow
(2) VideoFlow可以产生优秀的定性预测和定量结果, 优于最好VAE技术在无动作BAIR数据集上的随机视频预测结果
(3) 模型进一步直接优化了训练视频的 likelihood,使我们能够根据 likelihood 值直接评估其性能,执行精确的推理,并在推理和生成过程中具有较好的计算效率
设计
预备知识
在基于流的生成模型中, 数据首先从一个潜在空间(latent space) p θ ( z ) p_θ(z) pθ(z) 生成,然后通过可逆变换 g θ g_θ gθ 转换为 x \mathbf{x} x:
z ∼ p θ ( z ) ( 1 ) x = g θ ( z ) ( 2 ) \begin{aligned} &\mathbf{z} \sim p_{\theta}(\mathbf{z}) \ \ \ \ \ \ \ \ \ (1) \\ &\mathbf{x}=\mathbf{g}_{\theta}(\mathbf{z}) \ \ \ \ \ \ \ \ \ (2) \end{aligned} z∼pθ(z) (1)x=gθ(z) (2)
式中 z z z 为潜变量, p θ ( z ) p_θ(z) pθ(z)具有简单易处理的密度,如球形多元高斯分布 p θ ( z ) = N ( z ; 0 , I ) p_θ(z) = N (z; 0, I) pθ(z)=N(z;0,I). 给定一个数据点 x x x,通过 z = f θ ( x ) = g θ − 1 ( x ) z = f_θ(x) = g_θ^{−1}(x) z=fθ(x)=gθ−1(x) 进行潜在变量推断.
我们考虑 f f f (同样适用于 g g g) 是由一系列可逆变换组成: f = f 1 ◦ f 2 ◦ ⋅ ⋅ ⋅ ◦ f K f = f_1◦f_2◦···◦f_K f=f1◦f2◦⋅⋅⋅◦fK, 那么在式(2)的变量变化下,给定一个数据点,模型的概率密度函数 (probability density function, PDF) 可以写成
log p θ ( x ) = log p θ ( z ) + log ∣ det ( d z / d x ) ∣ = log p θ ( z ) + ∑ i = 1 K log ∣ det ( d h i / d h i − 1 ) ∣ ( 4 ) \begin{aligned} \log p_{\boldsymbol{\theta}}(\mathbf{x}) &=\log p_{\boldsymbol{\theta}}(\mathbf{z})+\log |\operatorname{det}(d \mathbf{z} / d \mathbf{x})| \\ &=\log p_{\boldsymbol{\theta}}(\mathbf{z})+\sum_{i=1}^{K} \log \left|\operatorname{det}\left(d \mathbf{h}_{i} / d \mathbf{h}_{i-1}\right)\right| \ \ \ \ \ \ \ \ \ \ \ \ (4) \end{aligned} logpθ(x)=logpθ(z)+log∣det(dz/dx)∣=logpθ(z)+i=1∑Klog∣det(dhi/dhi−1)∣ (4)
其中 h 0 ≜ x h_0 \triangleq x h0≜x, h K ≜ z h_K \triangleq z hK≜z. ∣ d e t ( d h i / d h i − 1 ) ∣ |det(dh_i/dh_{i−1})| ∣det(dhi/dhi−1)∣是雅可比矩阵 d h i / d h i − 1 dh_i/dh_{i−1} dhi/dhi−1 的行列式的绝对值, h i − 1 h_{i-1} hi−1和 h i h_i hi是经过 f i f_i fi的转换变量.
论文选择雅可比矩阵为三角矩阵/对角矩阵/置换矩阵的转换函数 f i f_i fi 来提高计算效率, 置换矩阵的雅克比行列式就是1, 而三角矩阵和对角矩阵的雅克比行列式为对角元素乘积 l o g ∣ d e t ( L ) ∣ = Σ j l o g ∣ L j , j ∣ log|det(L)| = \Sigma_j log|L_{j,j}| log∣det(L)∣=Σjlog∣Lj,j∣.
VideoFlow 模型
在论文的模型中,将潜在空间 z z z分解为每个时间步单独的潜在变量: z = { z t } t = 1 T z = \{z_t\}^T_{t=1} z={ zt}t=1T. x t x_t xt 是 z t z_t zt 在时间步 t t t 下对应视频帧的可逆转换: x t = g θ ( z t ) x_t = g_\theta(z_t) xt=gθ(zt).
模型使用一个多尺度的架构, 潜在变量 z t z_t zt 由多个层次的堆栈组成, 其中每个层次 l l l 在特定的尺度上编码关于帧 x t x_t xt 的信息: z t = { z t ( l ) } l = 1 L \mathbf{z}_t = \{\mathbf{z}^{(l)}_t\}^L_{l=1} zt={ zt(l)}l=1L, 每层一个组成元素 z t ( l ) z_t^{(l)} zt(l).
模型还需要一个 latent prior, 则对 latent prior 使用以下自回归因子分解:
p θ ( z ) = Π t = 1 T p θ ( z ∣ z < t ) ( 6 ) p_\theta(\mathbf{z}) = \Pi_{t=1}^T p_\theta(\mathbf{z} | \mathbf{z}_{<t}) \ \ \ \ \ \ \ \ \ \ \ \ (6) pθ(z)=Πt=1Tpθ(z∣z<t) (6)
其中 z \mathbf{z} z表示在 t t t 时间步之前的潜在变量帧 { z 1 , . . . , z t − 1 } \{z_1, ..., z_{t-1}\} { z1,...,zt−1}. 条件先验具有以下因数分解
p θ ( z t ∣ z < t ) = ∏ l = 1 L p θ ( z t ( l ) ∣ z < t ( l ) , z t ( > l ) ) ( 7 ) p_{\boldsymbol{\theta}}\left(\mathbf{z}_{t} \mid \mathbf{z}_{<t}\right)=\prod_{l=1}^{L} p_{\boldsymbol{\theta}}\left(\mathbf{z}_{t}^{(l)} \mid \mathbf{z}_{<t}^{(l)}, \mathbf{z}_{t}^{(>l)}\right) \ \ \ \ \ \ \ \ \ \ \ \ (7) pθ(zt∣z<t)=l=1∏Lpθ(zt(l)∣z<t(l),zt(>l)) (7)
其中 z < t ( l ) \mathbf{z}^{(l)}_{<t} z<t(l) 是上一个时间步的同level的潜在变量集合, z t ( > l ) \mathbf{z}^{(>l)}_{t} zt(>l) 是同时间步 t t t 的比 l l l 更高level的潜在变量集合. 示意图如下
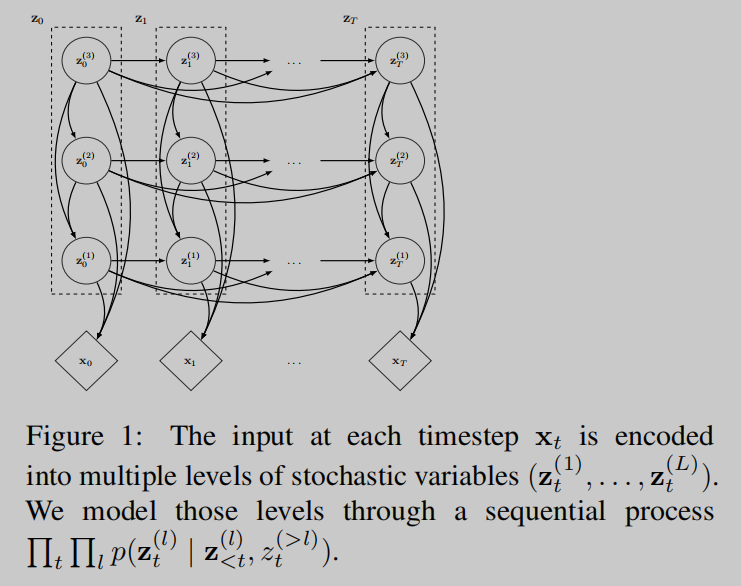
然后令每一个 p θ ( z t ( l ) ∣ z < t ( l ) , z t ( > l ) ) p_{\boldsymbol{\theta}}\left(\mathbf{z}_{t}^{(l)} \mid \mathbf{z}_{<t}^{(l)}, \mathbf{z}_{t}^{(>l)}\right) pθ(zt(l)∣z<t(l),zt(>l)) 为高斯密度的条件分解:
p θ ( z t ( l ) ∣ z < t ( l ) , z t ( > l ) ) = N ( z t ( l ) ; μ , σ ) ( 8 ) where ( μ , log σ ) = N N θ ( z < t ( l ) , z t ( > l ) ) \begin{aligned} p_{\boldsymbol{\theta}}\left(\mathbf{z}_{t}^{(l)} \mid \mathbf{z}_{<t}^{(l)}, \mathbf{z}_{t}^{(>l)}\right) &=\mathcal{N}\left(\mathbf{z}_{t}^{(l)} ; \boldsymbol{\mu}, \sigma\right) \ \ \ \ \ \ \ \ \ \ \ \ (8) \\ \text { where }(\boldsymbol{\mu}, \log \sigma) &=N N_{\boldsymbol{\theta}}\left(\mathbf{z}_{<t}^{(l)}, \mathbf{z}_{t}^{(>l)}\right) \end{aligned} pθ(zt(l)∣z<t(l),zt(>l)) where (μ,logσ)=N(zt(l);μ,σ) (8)=NNθ(z<t(l),zt(>l))
其中 N N θ ( ) NN_θ() NNθ() 是深度残差网络
实验
随机运动数据集的视频生成
dataset: 采用(Babaeizadeh et al., 2017)论文的dataset.
在这个数据集中,每个视频的第一帧包含一个形状,放置在一个64x64x3分辨率的灰色背景的中心附近,其类型、大小和颜色被随机采样。然后这个形状会向八个随机方向中的一个移动。由于形状以均匀的速度移动,我们应该能够使用它在第t步的位置来模拟形状在第(t + 1)步的位置。在 t = 2 时,形状的位置是概率的,对于任何其他的t,给定之前的时间步,位置是确定的。
用VideoFlow进行视频预测, 在生成以第一帧为中心形状的视频时,可以观察到模型一致地预测形状的未来轨迹是8个随机方向之一.
BAIR数据集的视频生成
使用BAIR机器人数据集的无动作版本(Ebert et al., 2017),其中包含分辨率为64x64的Sawyer机械臂视频。
使用 公式(6) 训练VideoFlow模型,给定前3帧的条件下给出帧4到帧13对数似然的无偏估计. 作者首先计算前3帧窗口的每像素位。然后在所有10帧目标帧和测试集上平均这些数据。结果报告测试集上的值为1.87 bpp (bits per pixel).
与随机视频生成baselines的比较
论文比较了两种最先进的随机视频生成模型,SAVP-VAE (Lee et al., 2018) 和 SV2P (Babaeizadeh et al., 2017)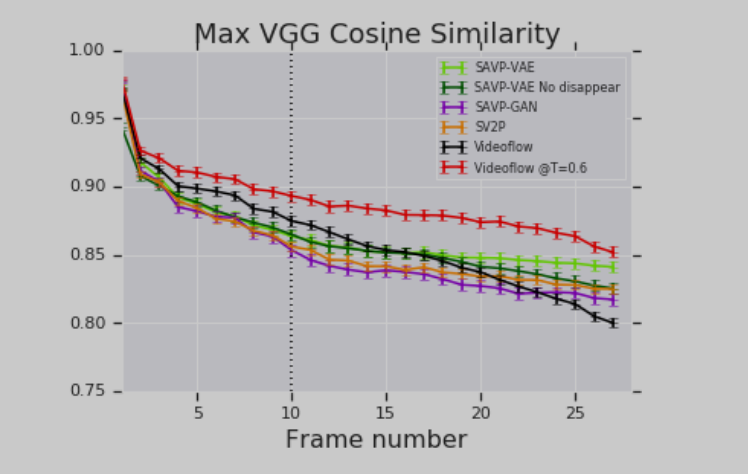
VideoFlow在T= 1.0与其他随机模型性能相当, 而当T = 0.6时获得更好的性能.
更长时间的预测
以前13帧作为条件, 生成到100帧, 上一行是无遮挡, 下一行是有遮挡时生成的视频帧
即使在100帧之后,生成的帧仍然保留在图像流形中,保持时间一致性。在遮挡存在的情况下,手臂轮廓依然非常清晰,但背景物体变得扭曲.
失序检测
为了探索预测的多个帧之间失序的可能性, 将测试集视频的前三帧作为模型的条件, 获取第4帧的分布函数 P ( X 4 ∣ X < 4 ) P(X_4|X_{<4}) P(X4∣X<4), 然后用这个分布计算第4帧之后的帧的出现在 t = 4时间步的可能性.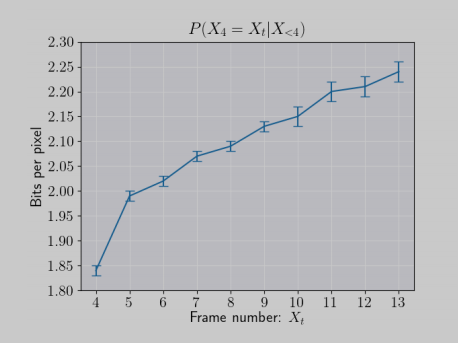
实验结果表明VideoFlow对多个帧的预测的 log-likelihood 是随着时间单调递减的 (bpp越低预测质量越高, 相应log-likelihood越高), 因此时间序越小的预测帧更可能出现在帧4的位置, 所以不容易出现预测帧时序的情况.
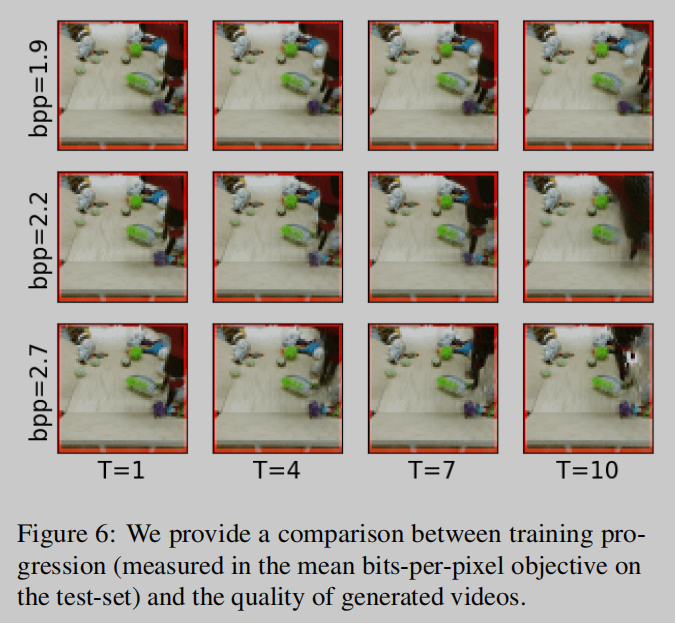
当接近较低的bpp时,VideoFlow模型可以得到高质量建模手臂的结构以及运动.
温度影响
作者研究了温度对BAIR数据集生成视频质量的影响。在较低的温度下,机械臂表现出较慢的运动和较低的不确定性,背景物体保持静止。在较高的温度下,机械臂表现出带有更多不确定性的随机运动,背景物体变得更嘈杂。
(论文的 temperature 是调整到验证集的 [0.1, 1.0] 的线性区间
总结
Related Works
Babaeizadeh, M., Finn, C., Erhan, D., Campbell, R. H., and Levine, S. Stochastic variational video prediction. arXiv
preprint arXiv:1710.11252, 2017.
Ebert, F., Finn, C., Lee, A. X., and Levine, S. Selfsupervised visual planning with temporal skip connections. arXiv preprint arXiv:1710.05268, 2017.
Lee, A. X., Zhang, R., Ebert, F., Abbeel, P., Finn, C., and Levine, S. Stochastic adversarial video prediction. arXiv
preprint arXiv:1804.01523, 2018.
Babaeizadeh, M., Finn, C., Erhan, D., Campbell, R. H., and Levine, S. Stochastic variational video prediction. arXiv
preprint arXiv:1710.11252, 2017.
Insights
(1) VideoFlow视频生成模型依赖于前n帧的信息进行未来帧的预测, 通过构造转换器 f f f 引入可证安全 (?
(2) 可以在生成的视频帧上运用图像隐写隐藏信息 (有点牵强
边栏推荐
猜你喜欢

浅谈混迹力扣和codeforces上的几个月
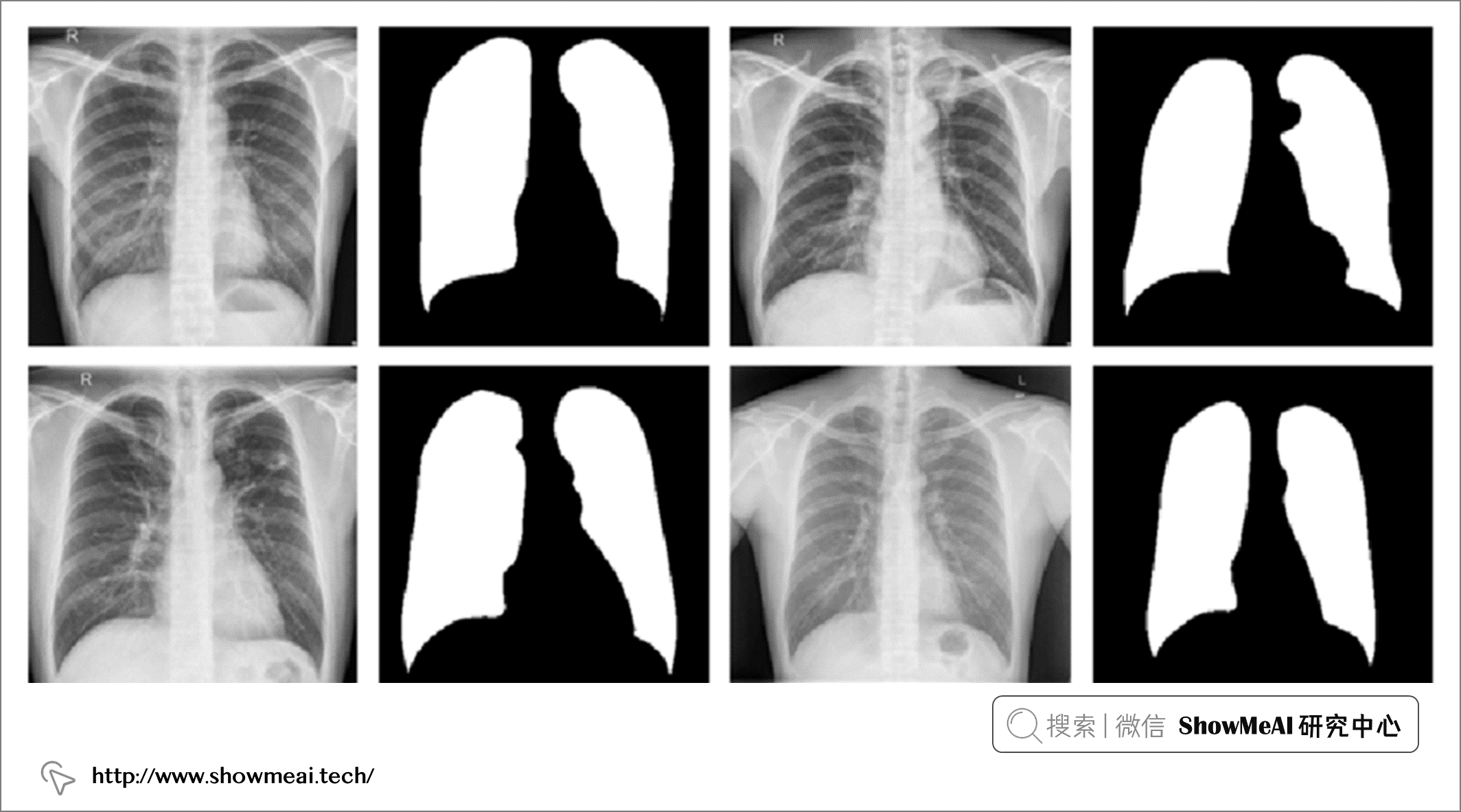
AI+医疗:使用神经网络进行医学影像识别分析
LeetCode 2349. 设计数字容器系统(SortedSet)
redis总结_多级缓存

Wechat Gymnasium Appointment Mini Program Graduation Design Finished Works Mini Program Graduation Design Finished Work (6) Question Opening Reply PPT

MySQL命令(命令行方式,而非图形界面方式)
Win11dll文件缺失怎么修复?Win11系统dll文件丢失的解决方法
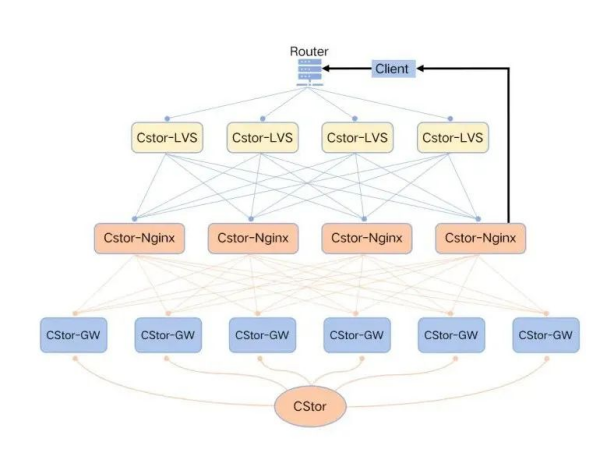
玩转云端 | 天翼云对象存储ZOS高可用的关键技术揭秘
Wechat Gymnasium Appointment Mini Program Graduation Design Finished Works (7) Mid-term Inspection Report
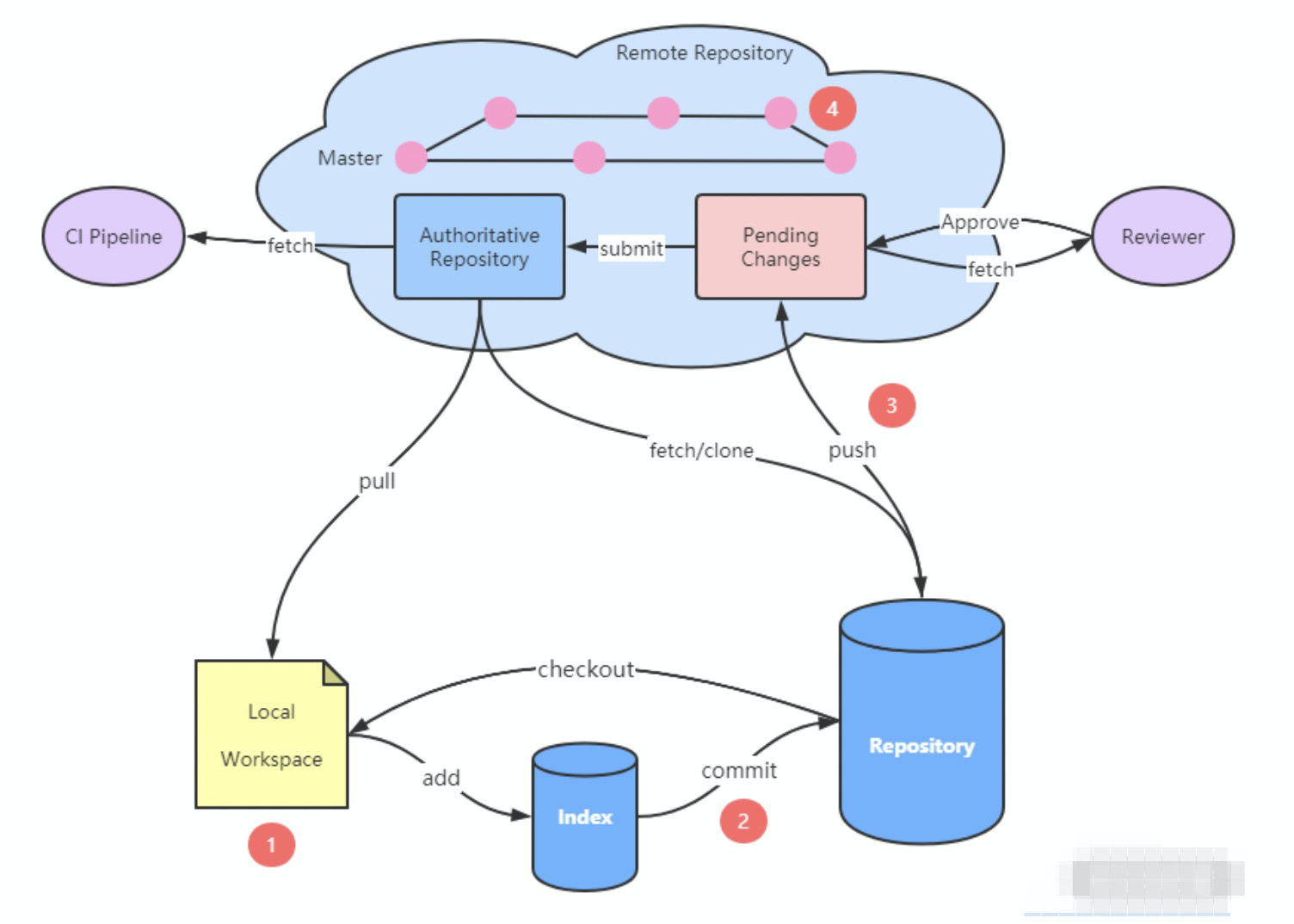
DevOps之代码检查
随机推荐
Technical life | How to draw a big picture of business
发挥云网融合优势,天翼云为政企铺设数字化转型跑道
How Tencent architects explained: The principle of Redis high-performance communication (essential version)
TSF微服务治理实战系列(一)——治理蓝图
E-Surfing Cloud 4.0 Distributed Cloud Enables Digital Transformation of Thousands of Industries
多聚体/壳聚糖修饰白蛋白纳米球/mPEG-HSA聚乙二醇人血清白蛋白纳米球的制备与研究
“12306”的架构到底有多牛逼?
【软考软件评测师】基于经验的测试技术
golang刷leetcode 字符串(4)逆波兰式
Redis总结_实战篇
How a "cloud" can bring about new changes in the industry
成功部署工业物联网的五个关键
知识点滴 - 什么是iAP2 (上)
mongodb的游标
LeetCode 2333. 最小差值平方和(贪心)
LeetCode 2353. 设计食物评分系统(sortedcontainers)
cache2go-源码阅读
golang源码分析(33)pollFD
分布式 | dble 启动的时候做了什么之配置检测
一文看懂推荐系统:概要01:推荐系统的基本概念