当前位置:网站首页>Strange way of expressing integers (expanding Chinese remainder theorem)
Strange way of expressing integers (expanding Chinese remainder theorem)
2022-07-03 20:25:00 【MangataTS】
Topic link
https://www.acwing.com/problem/content/description/206/
Ideas
For this question , We have to solve n An equation that satisfies the condition , We first consider the case of satisfying two equations :
X ≡ m 1 m o d a 1 X≡m_1 \ mod \ a_1 X≡m1 mod a1
X ≡ m 2 m o d a 2 X≡m_2 \ mod \ a_2 X≡m2 mod a2
This equation can also be written in the following format , Assume an arbitrary integer k i k_i ki
X ≡ k i a i + m i m o d a i X≡k_i a_i + m_i \ mod \ a_i X≡kiai+mi mod ai
So we get :
k 1 a 1 + m 1 = k 2 a 2 + m 2 k_1a_1 + m_1 = k_2 a_2 + m_2 k1a1+m1=k2a2+m2
namely k 1 a 1 − k 2 a 2 = m 2 − m 1 k_1a_1-k_2a_2=m_2-m_1 k1a1−k2a2=m2−m1
set up d by g c d ( a 1 , a 2 ) gcd(a_1,a_2) gcd(a1,a2)
If d ∣ m 2 − m 1 d |m_2-m_1 d∣m2−m1 Then the equation has a solution , We can solve by extending Euclidean algorithm k1,k2 A solution of
set up p For any integer , And because the solution is not unique , So we can put k1 The general solution of is written in the form :
k 1 = k 1 + p a 2 d k1 = k1 + p\frac{a_2}{d} k1=k1+pda2
Empathy k2 The general solution of can be written as :
k 2 = k 2 + p a 1 d k2 = k2 + p\frac{a_1}{d} k2=k2+pda1
Then we will k1 The general solution formula can be substituted into the original equation :
X ≡ ( ( k 1 + p a 2 d ) a 1 + m 1 ) m o d a 1 X≡((k_1 + p\frac{a_2}{d})a_1 + m1) \ mod \ a_1 X≡((k1+pda2)a1+m1) mod a1
X ≡ ( P a 1 ∗ a 2 d + a 1 k 1 + m 1 ) m o d a 1 X≡ (P\frac{a_1*a_2}{d} + a_1k_1 + m_1) \ mod \ a_1 X≡(Pda1∗a2+a1k1+m1) mod a1
X ≡ ( P × l g m ( a 1 , a 2 ) + ( a 1 k 1 + m 1 ) ) m o d a 1 X≡(P\times lgm(a_1,a_2) + (a_1k_1 + m_1)) \ mod \ a_1 X≡(P×lgm(a1,a2)+(a1k1+m1)) mod a1
Then at this time, we were surprised to find that this is not the format of the formula we began to transform , So we found that we can merge the two equations through this operation , Then we will n The equations are merged into one equation , In the end X ≡ P X 0 + m 1 m o d X 0 X≡P X_0 + m_1 \ mod \ X_0 X≡PX0+m1 mod X0 So direct output m 1 m_1 m1 Just fine
Be careful :
1. Because the data is very limited, we should ensure that k1 Is a minimum positive number solution
2. final m 1 m_1 m1 It could be negative , It's best to take the mold first, then add the modulus, and then take the mold , Guarantee non negative
Code
#include<bits/stdc++.h>
using namespace std;
//---------------- Custom part ----------------
#define ll long long
#define mod 1000000007
#define endl "\n"
#define PII pair<int,int>
#define INF 0x3f3f3f3f
int dx[4] = {
-1, 0, 1, 0}, dy[4] = {
0, 1, 0, -1};
ll ksm(ll a,ll b) {
ll ans = 1;
for(;b;b>>=1LL) {
if(b & 1) ans = ans * a % mod;
a = a * a % mod;
}
return ans;
}
ll lowbit(ll x){
return -x & x;}
const int N = 2e6+10;
//---------------- Custom part ----------------
int t,n,m,q,a[N];
ll exgcd(ll a,ll b,ll &x,ll &y){
if(!b){
x = 1,y = 0;
return a;
}
ll d = exgcd(b,a%b,y,x);
y -= a/b * x;
return d;
}
void slove(){
cin>>n;
ll a1,m1;
cin>>a1>>m1;
bool fg = true;
for(int i = 1;i < n; ++i) {
ll a2,m2;
cin>>a2>>m2;
ll k1,k2;
ll d = exgcd(a1,a2,k1,k2);
if((m2 - m1) % d){
fg = false;
break;
}
k1 *= (m2-m1)/d;// Double
ll t = abs(a2 / d);
k1 = (k1 % t + t) % t;// Become the smallest positive integer solution, otherwise it will overflow
m1 = a1 * k1 + m1;
a1 = (a1 / d * a2);
}
if(fg){
cout<< (m1 % a1 + a1) % a1 <<endl;
}
else{
cout<< "-1"<<endl;
}
}
int main()
{
ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
t = 1;
while(t--){
slove();
}
return 0;
}
边栏推荐
- Plan for the first half of 2022 -- pass the PMP Exam
- About callback function and hook function
- 强基计划 数学相关书籍 推荐
- 6. Data agent object Defineproperty method
- Teach you how to quickly recover data by deleting recycle bin files by mistake
- Initialization and instantiation
- Pytorch sets the weight and bias of the model to zero
- Deep search DFS + wide search BFS + traversal of trees and graphs + topological sequence (template article acwing)
- An old programmer gave it to college students
- February 14-20, 2022 (osgear source code debugging +ue4 video +ogremain source code transcription)
猜你喜欢
Exercises of function recursion

IP address is such an important knowledge that it's useless to listen to a younger student?

浅议.NET遗留应用改造
Detailed and not wordy. Share the win10 tutorial of computer reinstallation system

Gym welcomes the first complete environmental document, which makes it easier to get started with intensive learning!

Acquisition and transmission of parameters in automatic testing of JMeter interface
JMeter connection database
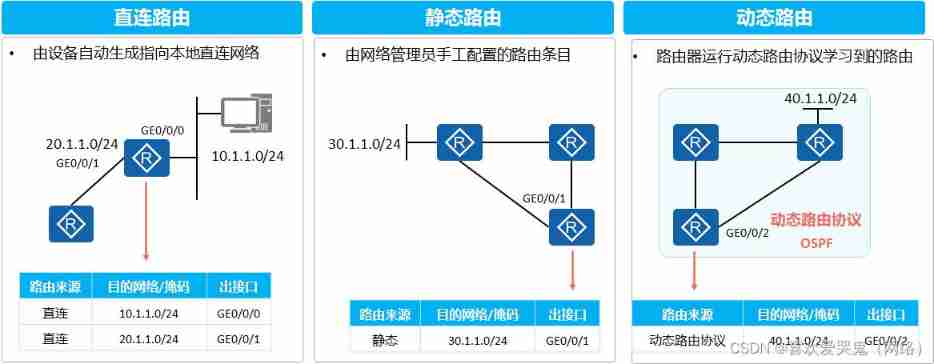
Popularize the basics of IP routing

Test panghu was teaching you how to use the technical code to flirt with girls online on Valentine's Day 520

Today's work summary and plan: February 14, 2022
随机推荐
MySQL dump - exclude some table data - MySQL dump - exclude some table data
Global and Chinese market of high temperature Silver sintering paste 2022-2028: Research Report on technology, participants, trends, market size and share
Realize user registration and login
44. Concurrent programming theory
Gym welcomes the first complete environmental document, which makes it easier to get started with intensive learning!
5. MVVM model
Global and Chinese market of high purity copper foil 2022-2028: Research Report on technology, participants, trends, market size and share
Rd file name conflict when extending a S4 method of some other package
Micro service knowledge sorting - cache technology
Phpexcel import export
2166. Design bit set
MySQL 8.0 data backup and recovery
Nerfplusplus parameter format sorting
1.4 learn more about functions
Global and Chinese markets of active matrix LCD 2022-2028: Research Report on technology, participants, trends, market size and share
Today's work summary and plan: February 14, 2022
What is the difference between a kill process and a close process- What are the differences between kill process and close process?
Node MySQL serialize cannot rollback transactions
Task of gradle learning
你真的知道自己多大了吗?