Brute force recursion to dynamic programming 07 (516. Longest palindrome subsequence)

516.最长回文子序列

力扣题目链接

给定一个字符串 s ,找到其中最长的回文子序列,并返回该序列的长度.可以假设 s 的最大长度为 1000 .

示例 1:
输入: “bbbab”
输出: 4
一个可能的最长回文子序列为 “bbbb”.

示例 2:
输入:“cbbd”
输出: 2
一个可能的最长回文子序列为 “bb”.

提示：

• 1 <= s.length <= 1000
• s 只包含小写英文字母

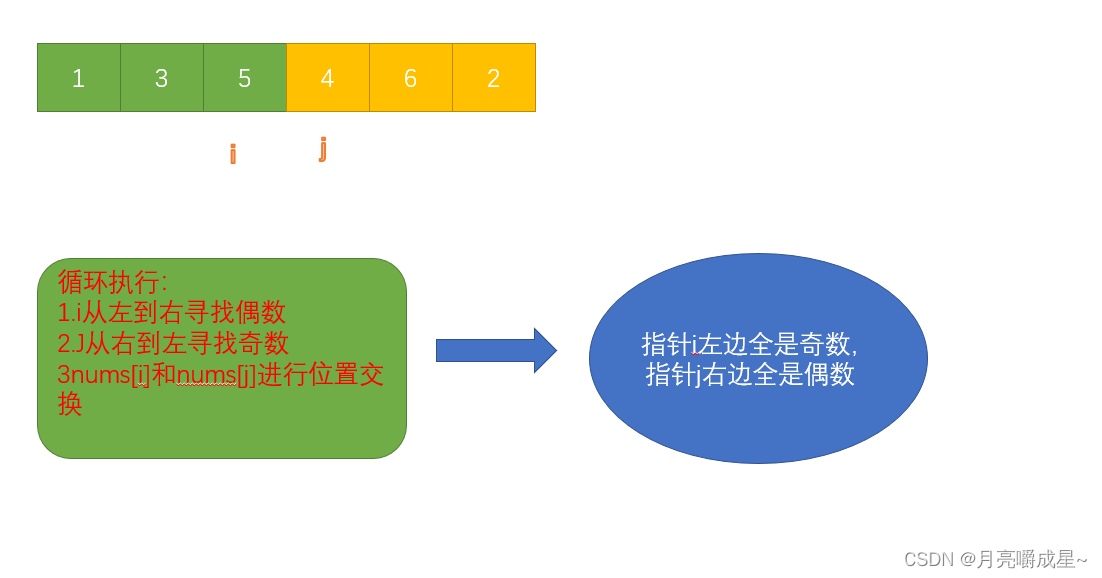
暴力递归

Start comparing left and right,If left and right are the same position,That must be a palindrome sequence,返回1,If left and right are adjacent,如果左右相等,则返回2 ,Because both are members of a palindrome subsequence;否则返回1,两个只有1can be a member of a palindromic subsequence.
其他情况：

不以 L 开头,不以 R 结尾
以 L 开头,不以 R 结尾
不以 L 开头,以 R 结尾
以 L 开头,以 R 结尾 （This is to compare whether this situation exists or not,There are immediate consequences+2,Both are members of the result）
Take the largest of the four

    public int longestPalindromeSubseq(String s) {
    
        return process(s.toCharArray(), 0, s.length() - 1);
    }

    public int process(char[] s, int L, int R) {
    
        if (L == R) {
    
            return 1;
        } else if (L + 1 == R) {
    
            //如果只有两位 0 和 1 位
            return s[L] == s[R] ? 2 : 1;
        } else {
    
            //其他情况
            //以不以L开头 不以R结尾
            int NLNR = process(s, L + 1, R - 1);
            //以L开头,不以R结尾
            int LNR = process(s, L, R - 1);
            //不以L开头,以R结尾
            int NLR = process(s, L + 1, R);
            //以L开头,以R结尾
            int LR = s[L] == s[R] ? 2 + process(s, L + 1, R - 1) : 0;
            return Math.max(Math.max(NLNR, LNR), Math.max(NLR, LR));
        }
    }

动态规划

First deal with the diagonal and the lines above the diagonal
Diagonally self and self are definitely palindromic,值为1
The latter if equal to the former,Then both are members of the palindrome,返回2,Otherwise one of them is a member of the palindrome,返回1.
从下往上,从左往右计算,此时 j 至少是 i + 2 了.

    public int longestPalindromeSubseq2(String s) {
    
        int n = s.length();
        char[] chars = s.toCharArray();
        int[][] dp = new int[n][n];
        dp[n - 1][n - 1] = 1;
        for (int i = 0; i < n - 1; i++) {
    
            //When an element is on the main diagonal,Must be equal to the current one,即为1
            dp[i][i] = 1;
            //A line on the main diagonal
            dp[i][i + 1] = chars[i] == chars[i + 1] ? 2 : 1;
        }
        for (int i = n - 3; i >= 0; i--) {
    
            for (int j = i + 2; j < n; j++) {
    
                //其他情况
                //以不以L开头 不以R结尾
                int NLNR = dp[i + 1][j - 1];
                //以L开头,不以R结尾
                int LNR = dp[i][j - 1];
                //不以L开头,以R结尾
                int NLR = dp[i + 1][j];
                //以L开头,以R结尾
                int LR = chars[i] == chars[j] ? 2 + dp[i + 1][j - 1] : 0;
                dp[i][j] = Math.max(Math.max(NLNR, LNR), Math.max(NLR, LR));
            }
        }

        return dp[0][n - 1];
    }