动态规划问题(四)

一、矩阵的最小路径和

解法:动态规划

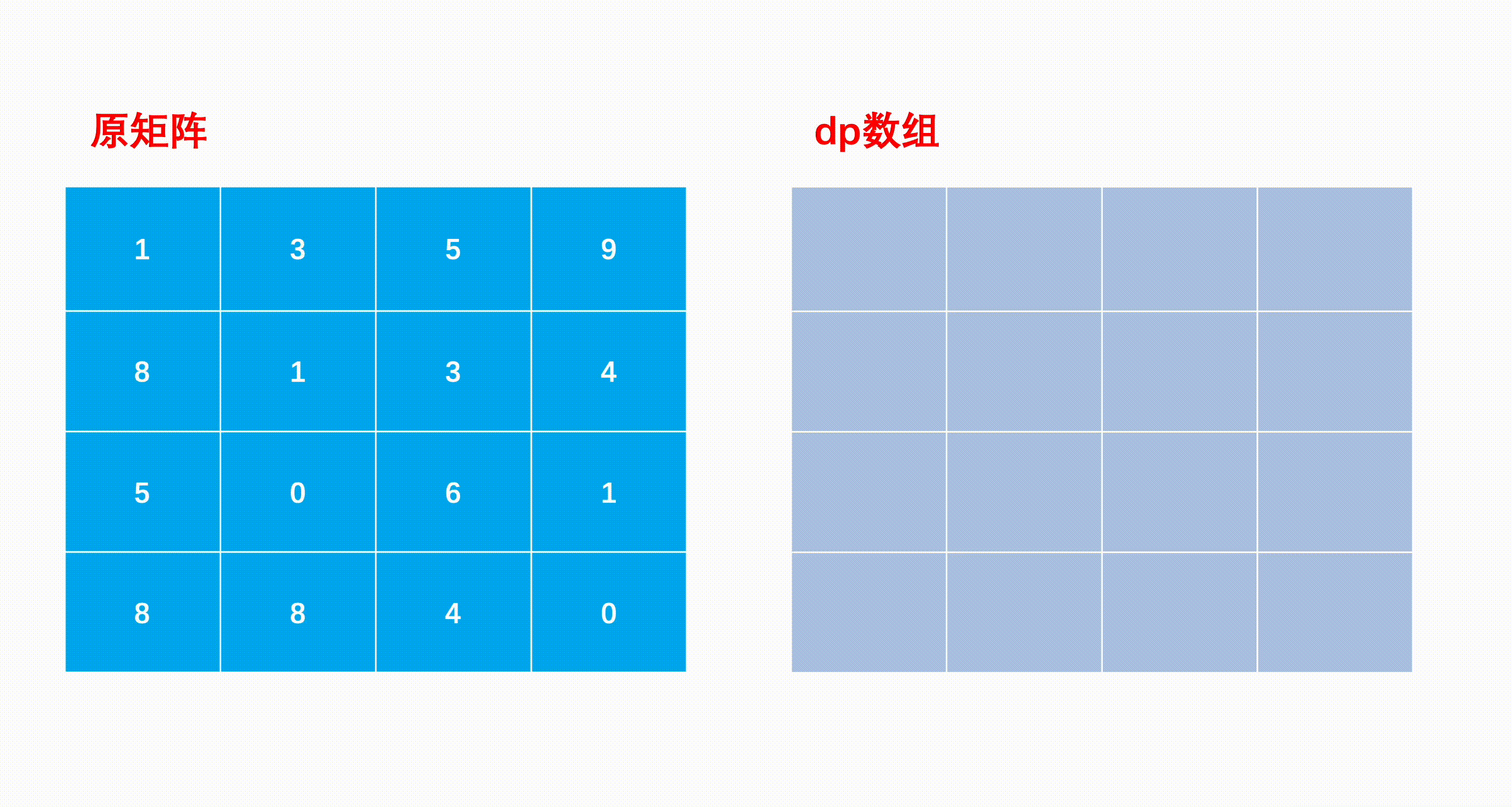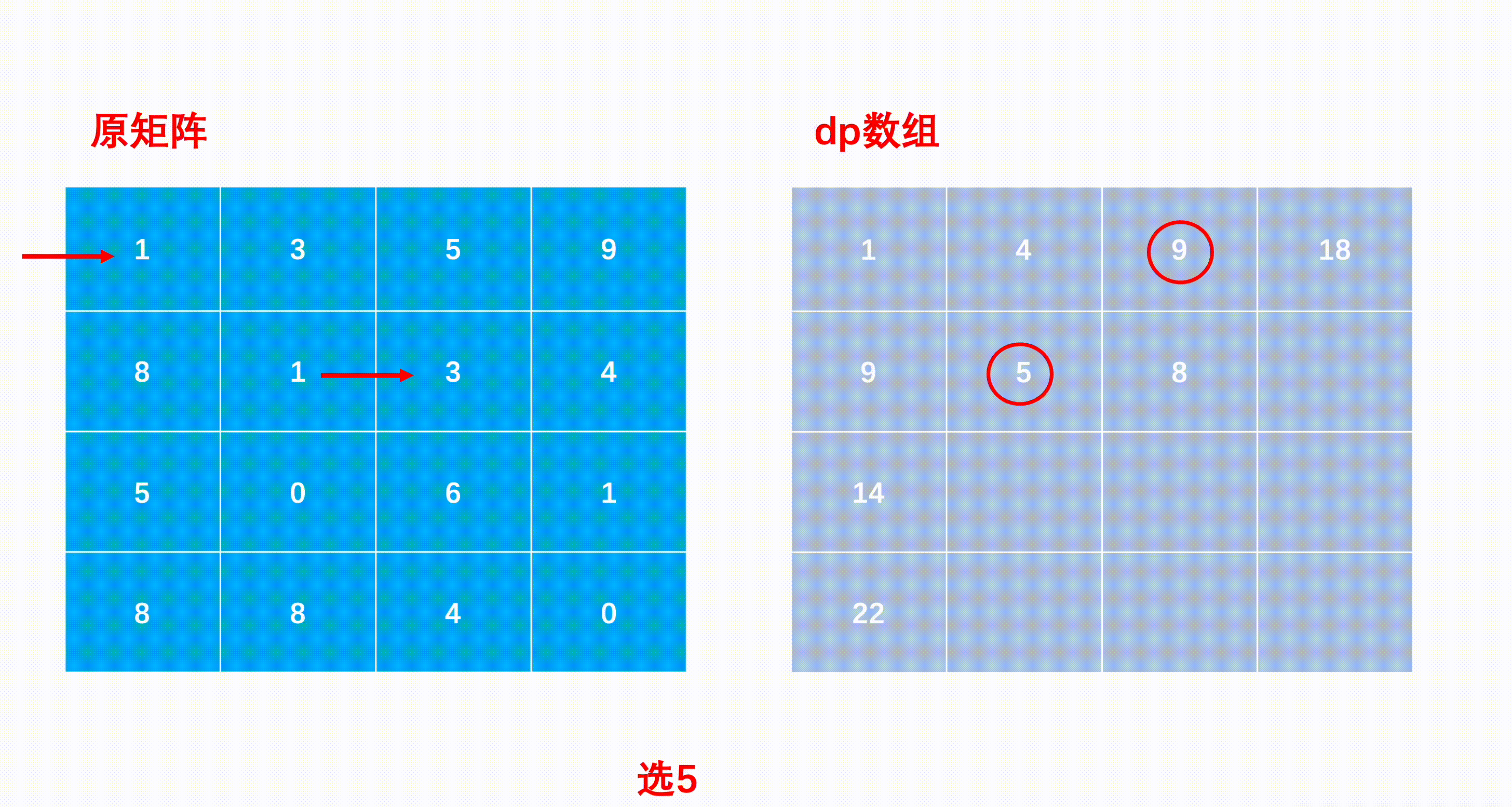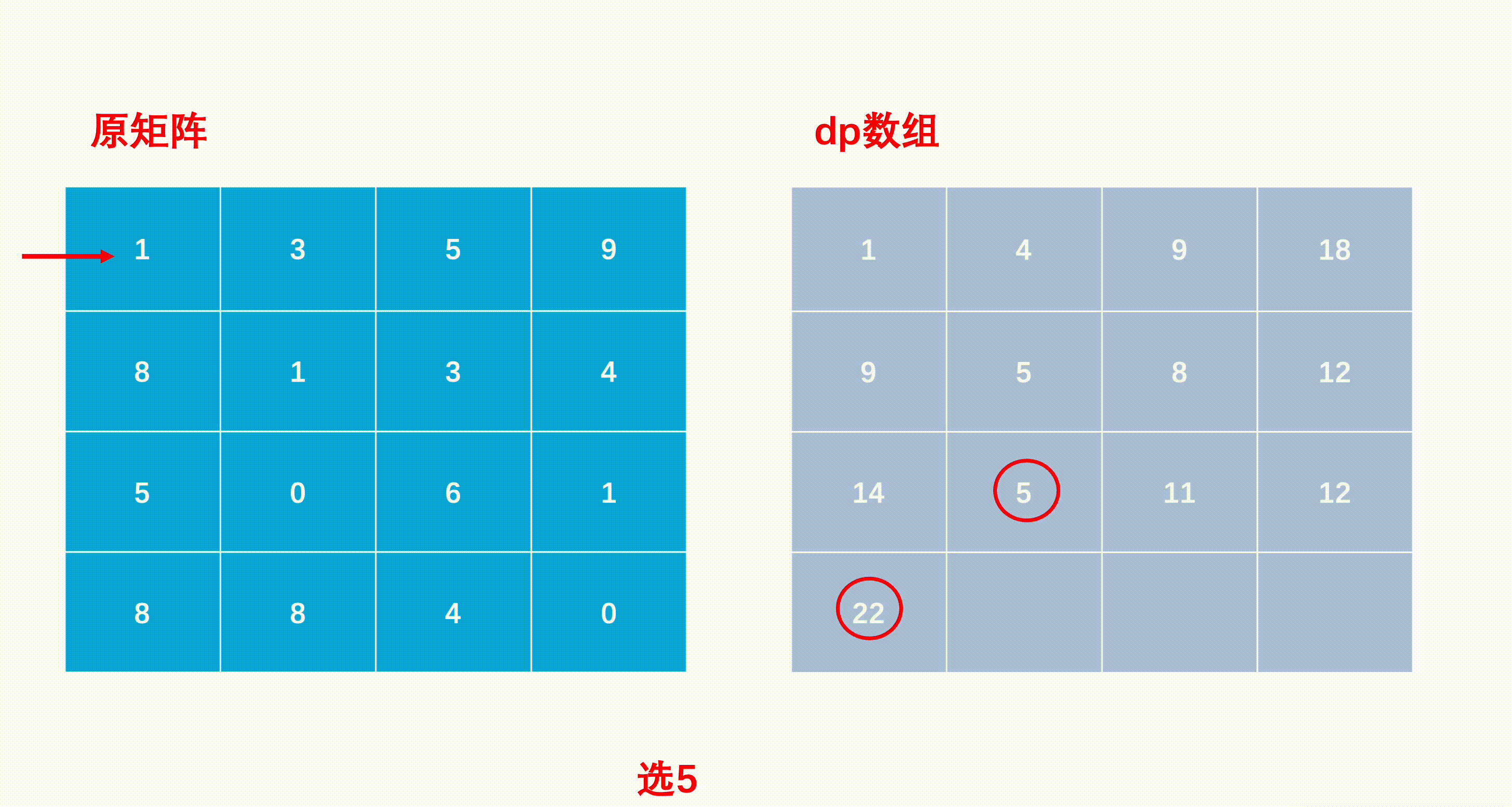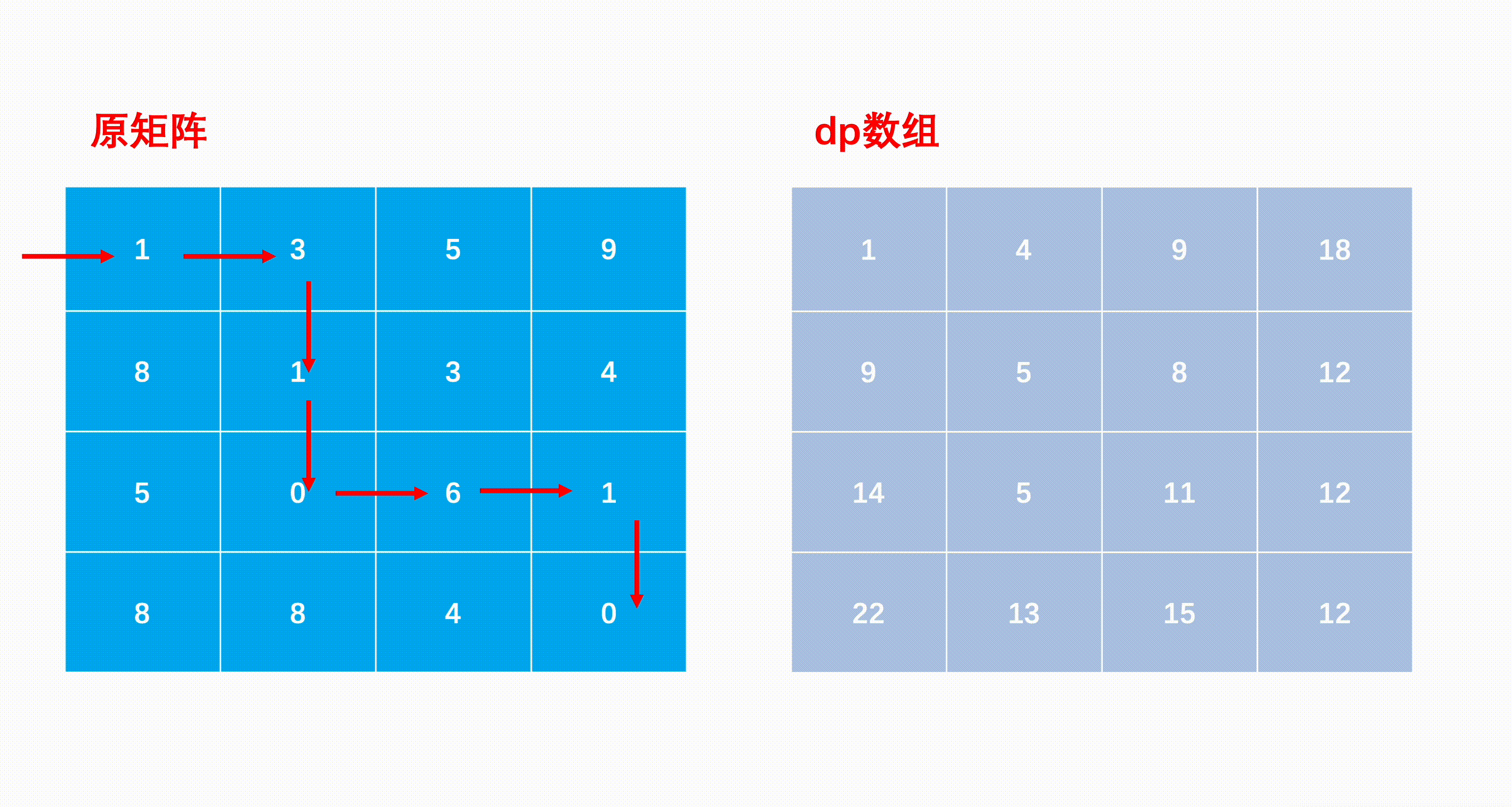
• 我们可以构造一个与矩阵同样大小的二维辅助数组，其中dp[i][j]表示以(i,j)位置为终点的最短路径和，则dp[0][0]=matrix[0][0]
• 很容易知道第一行与第一列，只能分别向右或向下，没有第二种选择，因此第一行只能由其左边的累加，第一列只能由其上面的累加。
• 边缘状态构造好以后，遍历矩阵，补全矩阵中每个位置的dp数组值：如果当前的位置是(i，j)，上一步要么是(i−1,j)往下，要么就是(i,j−1)往右，那么取其中较小值与当前位置的值相加就是到当前位置的最小路径和，因此状态转移公式为dp[i][j]=min(dp[i−1][j],dp[i][j−1])+matrix[i][j]
• 最后移动到(n−1,m−1)的位置就是到右下角的最短路径和
  

class Solution {
    
public:
    int minPathSum(vector<vector<int> >& matrix) {
    
        int n = matrix.size();
        //因为n,m均大于等于1
        int m = matrix[0].size();  
        //dp[i][j]表示以当前i，j位置为终点的最短路径长度
        vector<vector<int> > dp(n + 1, vector<int>(m + 1, 0));
        dp[0][0] = matrix[0][0];
        //处理第一列
        for(int i = 1; i < n; i++)
            dp[i][0] = matrix[i][0] + dp[i - 1][0];
        //处理第一行
        for(int j = 1; j < m; j++)
            dp[0][j] = matrix[0][j] + dp[0][j - 1];
        //其他按照公式来
        for(int i = 1; i < n; i++){
     
          for(int j = 1; j < m; j++){
    
              dp[i][j] = matrix[i][j] + (dp[i - 1][j] > dp[i][j - 1] ? dp[i][j - 1] : dp[i - 1][j]);
          }
      }
       return dp[n - 1][m - 1];
    }
};

时间复杂度：O(mn)，单独遍历矩阵的一行一列，然后遍历整个矩阵
空间复杂度：O(mn)，辅助矩阵dp为二维数组

二、把数字翻译成字符串

解法:动态规划

• 用辅助数组dp表示前i个数的译码方法有多少种。
• 对于一个数，我们可以直接译码它，也可以将其与前面的1或者2组合起来译码：如果直接译码，则dp[i]=dp[i−1]；如果组合译码，则dp[i]=dp[i−2]。
• 对于只有一种译码方式的，选上种dp[i−1即可，对于满足两种译码方式（10，20不能）则是dp[i−1]+dp[i−2]
• 依次相加，最后的dp[length]]即为所求答案。

class Solution {
    
public:
    int solve(string nums) {
    
        //排除0
        if(nums == "0")  
            return 0;
        //排除只有一种可能的10 和 20
        if(nums == "10" || nums == "20")  
            return 1;
        //当0的前面不是1或2时，无法译码，0种
        for(int i = 1; i < nums.length(); i++){
      
            if(nums[i] == '0')
                if(nums[i - 1] != '1' && nums[i - 1] != '2')
                    return 0;
        }
        //辅助数组初始化为1
        vector<int> dp(nums.length() + 1, 1);  
        for(int i = 2; i <= nums.length(); i++){
    
            //在11-19，21-26之间的情况
            if((nums[i - 2] == '1' && nums[i - 1] != '0') || (nums[i - 2] == '2' && nums[i - 1] > '0' && nums[i - 1] < '7'))
               dp[i] = dp[i - 1] + dp[i - 2];
            else
                dp[i] = dp[i - 1];
        }
        return dp[nums.length()];
    }
};

时间复杂度：O(n)，两次遍历都是单层
空间复杂度：O(n)，辅助数组dp

三、兑换零钱(一)

解法一:动态规划(推荐)

• 可以用dp[i]表示要凑出i元钱需要最小的货币数。
• 一开始都设置为最大值aim+1，因此货币最小1元，即货币数不会超过aim
• 初始化dp[0]=0。
• 后续遍历1元到aim元，枚举每种面值的货币都可能组成的情况，取每次的最小值即可，转移方程为dp[i]=min(dp[i],dp[i−arr[j]]+1)
• 最后比较dp[aim]的值是否超过aim，如果超过说明无解，否则返回即可。

class Solution {
    
public:
    int minMoney(vector<int>& arr, int aim) {
    
        //小于1的都返回0
        if(aim < 1) 
            return 0;
        //dp[i]表示凑齐i元最少需要多少货币数
        vector<int> dp(aim + 1, aim + 1);  
        dp[0] = 0; 
        //遍历1-aim元
        for(int i = 1; i <= aim; i++){
     
            //每种面值的货币都要枚举
            for(int j = 0; j < arr.size(); j++){
     
                //如果面值不超过要凑的钱才能用
                if(arr[j] <= i) 
                    //维护最小值
                    dp[i] = min(dp[i], dp[i - arr[j]] + 1); 
            }
        }
        //如果最终答案大于aim代表无解
        return dp[aim] > aim ? -1 : dp[aim]; 
    }
};

时间复杂度：O(n⋅aim)，第一层遍历枚举1元到aim元，第二层遍历枚举n种货币面值
空间复杂度：O(aim)，辅助数组dp的大小

解法二:空间记忆递归

对于需要凑成aim的钱，第一次我们可以选择使用arr[0]，则后续需要凑出aim−arr[0]的钱，那后续就是上一个的子问题，可以用递归进行。因为每种面值使用不受限，因此第一次我们可以使用arr数组中每一个，同理后续每次也可以使用arr数组中每一次，因此每次递归都要遍历arr数组，相当于分枝为arr.size()的树型递归。

• 递归的时候，一旦剩余需要凑出的钱为0，则找到一种情况，记录下整个的使用货币的数量，维护最小值即可。
• 一旦剩余需要凑出的钱为负，则意味着这一分枝无解，返回-1.
• 后续每次也可以使用arr数组中一次，进入子问题。
• 但是树型递归的复杂度需要O(aim^n)，重复计算过于多了，如图所示，因此我们可以用一个dp数组记录每次递归上来的结果，避免小分支重复计算，如果dp数组有值直接获取即可，不用再重复计算了。

class Solution {
    
public:
    int recursion(vector<int>& arr, int aim, vector<int>& dp){
    
        //组合超过了，返回-1
        if(aim < 0) 
            return -1;
        //组合刚好等于需要的零钱
        if(aim == 0) 
            return 0;
        //剩余零钱是否已经被运算过了
        if(dp[aim - 1] != 0) 
            return dp[aim - 1];
        int Min = INT_MAX;
        //遍历所有面值
        for(int i = 0; i < arr.size(); i++){
     
            //递归运算选择当前的面值
            int res = recursion(arr, aim - arr[i], dp); 
            //获取最小值
            if(res >= 0 && res < Min) 
                Min = res + 1;
        }
        //更新最小值
        dp[aim - 1] = Min == INT_MAX ? -1 : Min; 
        return dp[aim - 1];
    }
    int minMoney(vector<int>& arr, int aim) {
    
        //小于1的都返回0
        if(aim < 1) 
            return 0;
        //记录递归中间的值
        vector<int> dp(aim, 0); 
        return recursion(arr, aim, dp);
    }
};

时间复杂度：O(n⋅aim)，一共需要计算aim个状态的答案，每个状态需要枚举n个面值
空间复杂度：O(aim)，递归栈深度及辅助数组的空间