利用matlab求解线性优化问题【基于matlab的动力学模型学习笔记_11】

题目：

 （1）画出可行域范围

question1.m

%% 标出函数
r=4;
a1=0;
a2=0;
theta=0:pi/20:2*pi;
x_1=a1+r*cos(theta);
x_2=a2+r*sin(theta);
plot(x_1,x_2);
hold on
text(2,4,'16-(x_1)^2-(x_2)^2=0','color','b'); %在坐标点(6.8,4)显示x1=7这个函数线

L2=[-2,-4;5,3]; 
plot(L2(:,1),L2(:,2));hold on    %x2最大值为3
text(3,1,'2-x_1-x_2=0','color','b'); %从点L2(:,1)到点L2(:,2)

L3=[-5,0;5 0]; 
plot(L3(:,1),L3(:,2));hold on 
text(3,0,'x_1=0','color','b') 

L4=[0,-5;0,5]; 
plot(L4(:,1),L4(:,2)); 
text(0,3,'x_2=0','color','b') 

grid on

%% 填充
[X1,X2]=meshgrid(0:0.01:5,0:0.01:5);%画出区域
idX1=(X1.*X1+X2.*X2<=16)&(-X2+X1<=2)&(X1>=0)&(X2>=0);
X1=X1(idX1);
X2=X2(idX1);
k=convhull(X1,X2); %计算面积
h=fill(X1(k),X2(k),'g');  %绿色填充        
set(h,'edgealpha',0,'facealpha',0.3)  %边界，透明度

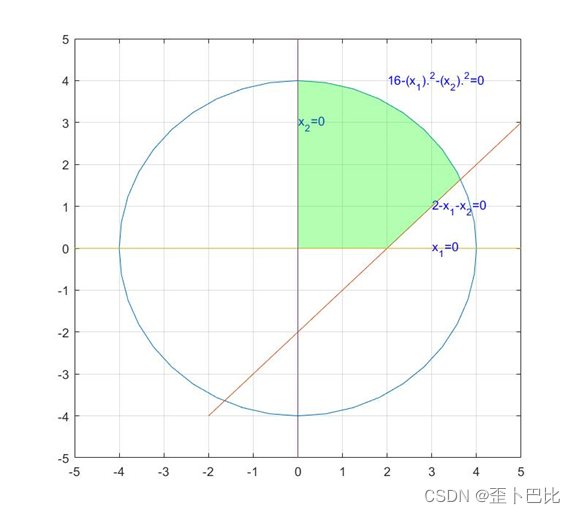
 （2）利用fmincon分别求解无约束、约束最优解

Matlab中的fmincon函数可以用于求解带约束的非线性多变量函数的最小值，这里用来求解此处的最优解。

fmincon函数参考：

Matlab求解非线性规划，fmincon函数的用法总结_小朱同学~的博客-CSDN博客_fmincon函数用法

官方帮助文档：https://ww2.mathworks.cn/help/optim/ug/fmincon.html? searchHighlight=fmincon&s_tid=srchtitle_fmincon_1

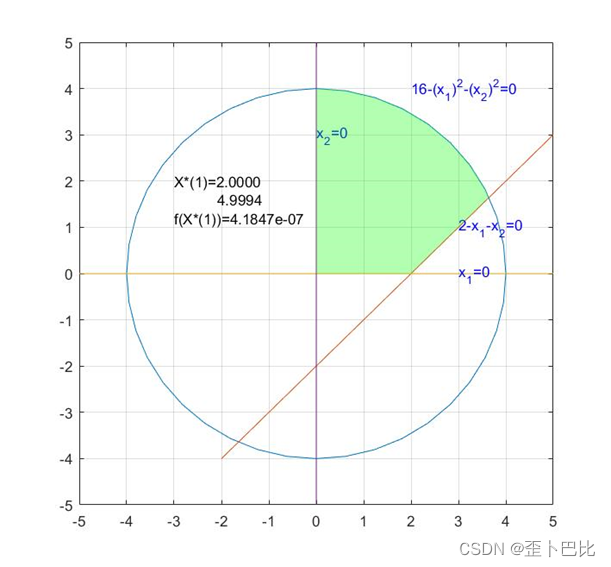
(2.1)无约束最优解

目标函数fun1.m：

%目标函数
function f=fun1(x)
f=(x(1)-2).^2+(x(2)-5).^2
end

无约束最优解question2_1.m：

%% 标出函数
r=4;
a1=0;
a2=0;
theta=0:pi/20:2*pi;
x_1=a1+r*cos(theta);
x_2=a2+r*sin(theta);
plot(x_1,x_2);
hold on
text(2,4,'16-(x_1)^2-(x_2)^2=0','color','b'); %在坐标点(6.8,4)显示x1=7这个函数线

L2=[-2,-4;5,3]; 
plot(L2(:,1),L2(:,2));hold on    %x2最大值为3
text(3,1,'2-x_1-x_2=0','color','b'); %从点L2(:,1)到点L2(:,2)

L3=[-5,0;5 0]; 
plot(L3(:,1),L3(:,2));hold on 
text(3,0,'x_1=0','color','b') 

L4=[0,-5;0,5]; 
plot(L4(:,1),L4(:,2)); 
text(0,3,'x_2=0','color','b') 

grid on

%% 填充
[X1,X2]=meshgrid(0:0.01:5,0:0.01:5);%画出区域
idX1=(X1.*X1+X2.*X2<=16)&(-X2+X1<=2)&(X1>=0)&(X2>=0);
X1=X1(idX1);
X2=X2(idX1);
k=convhull(X1,X2); %计算面积
h=fill(X1(k),X2(k),'g');  %绿色填充        
set(h,'edgealpha',0,'facealpha',0.3)  %边界，透明度


%问题2.1主函数
options=optimset;
x0=[0;0];%给定初值
lb=[0;0];%函数下限
ub=[5;5];%函数上限
[x,y]=fmincon('fun1',x0,[],[],[],[],lb,ub)

%加标注
text(-3,2,'X*(1)=2.0000') 
text(-2.1,1.6,'4.9994') 
text(-3,1.2,'f(X*(1))=4.1847e-07') 

 (2.2)约束最优解

目标函数fun1.m：

%目标函数
function f=fun1(x)
f=(x(1)-2).^2+(x(2)-5).^2
end

非线性约束条件函数fun2.m：

%非线性约束条件函数
function[g,h]=fun2(x)
%matlab中默认g<=0，若不对应需取反
g(1)=-16+x(2).^2+x(1).^2;
g(2)=-2+x(1)+x(2);
h=[];%没有等式约束的时候用空值代替
end

无约束最优解question2_2.m：

%% 标出函数
r=4;
a1=0;
a2=0;
theta=0:pi/20:2*pi;
x_1=a1+r*cos(theta);
x_2=a2+r*sin(theta);
plot(x_1,x_2);
hold on
text(2,4,'16-(x_1)^2-(x_2)^2=0','color','b'); %在坐标点(6.8,4)显示x1=7这个函数线

L2=[-2,-4;5,3]; 
plot(L2(:,1),L2(:,2));hold on    %x2最大值为3
text(3,1,'2-x_1-x_2=0','color','b'); %从点L2(:,1)到点L2(:,2)

L3=[-5,0;5 0]; 
plot(L3(:,1),L3(:,2));hold on 
text(3,0,'x_1=0','color','b') 

L4=[0,-5;0,5]; 
plot(L4(:,1),L4(:,2)); 
text(0,3,'x_2=0','color','b') 

grid on

%% 填充
[X1,X2]=meshgrid(0:0.01:5,0:0.01:5);%画出区域
idX1=(X1.*X1+X2.*X2<=16)&(-X2+X1<=2)&(X1>=0)&(X2>=0);
X1=X1(idX1);
X2=X2(idX1);
k=convhull(X1,X2); %计算面积
h=fill(X1(k),X2(k),'g');  %绿色填充        
set(h,'edgealpha',0,'facealpha',0.3)  %边界，透明度

%问题2.2主函数
options=optimset;
x0=[0;0];%给定初值
lb=[0;0];%函数下限
ub=[5;5];%函数上限
[x,y]=fmincon('fun1',x0,[],[],[],[],lb,ub,'fun2')

%加标注
text(-3,2,'X*(2)=0.0000') 
text(-2.1,1.6,'2.0000') 
text(-3,1.2,'f(X*(2))=13')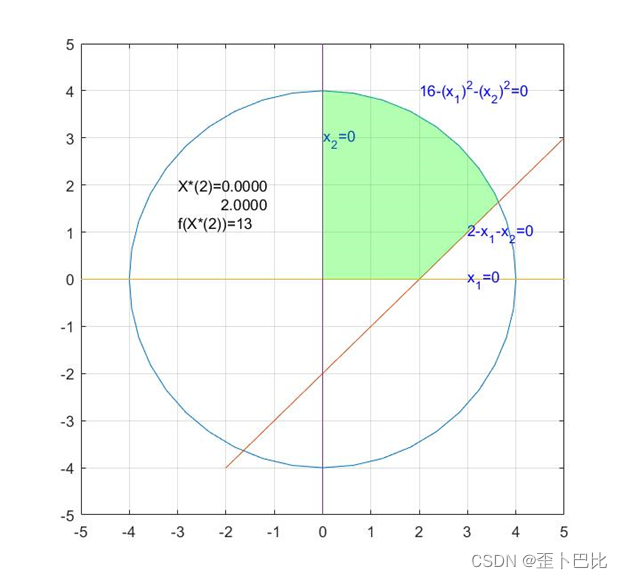 

 （3）线性约束最优解

目标函数fun1.m：

%目标函数
function f=fun1(x)
f=(x(1)-2).^2+(x(2)-5).^2
end

线性约束条件函数fun3.m：

%线性约束条件函数
function[g,h]=fun3(x)
%matlab中默认g<=0，若不对应需取反
g(1)=-16+x(2).^2+x(1).^2;
g(2)=-2+x(1)+x(2);

%线性约束条件
h=x(1)-x(2);
end

线性约束最优解question3.m：

%% 标出函数
r=4;
a1=0;
a2=0;
theta=0:pi/20:2*pi;
x_1=a1+r*cos(theta);
x_2=a2+r*sin(theta);
plot(x_1,x_2);
hold on
text(2,4,'16-(x_1)^2-(x_2)^2=0','color','b'); %在坐标点(6.8,4)显示x1=7这个函数线

L2=[-2,-4;5,3]; 
plot(L2(:,1),L2(:,2));hold on    %x2最大值为3
text(3,1,'2-x_1-x_2=0','color','b'); %从点L2(:,1)到点L2(:,2)

L3=[-5,0;5 0]; 
plot(L3(:,1),L3(:,2));hold on 
text(3,0,'x_1=0','color','b') 

L4=[0,-5;0,5]; 
plot(L4(:,1),L4(:,2)); 
text(0,3,'x_2=0','color','b') 

grid on

%% 填充
[X1,X2]=meshgrid(0:0.01:5,0:0.01:5);%画出区域
idX1=(X1.*X1+X2.*X2<=16)&(-X2+X1<=2)&(X1>=0)&(X2>=0);
X1=X1(idX1);
X2=X2(idX1);
k=convhull(X1,X2); %计算面积
h=fill(X1(k),X2(k),'g');  %绿色填充        
set(h,'edgealpha',0,'facealpha',0.3)  %边界，透明度
%问题3主函数
options=optimset;
x0=[0;0];%给定初值
lb=[0;0];%函数下限
ub=[5;5];%函数上限
[x,y]=fmincon('fun1',x0,[],[],[],[],lb,ub,'fun3')

%加标注
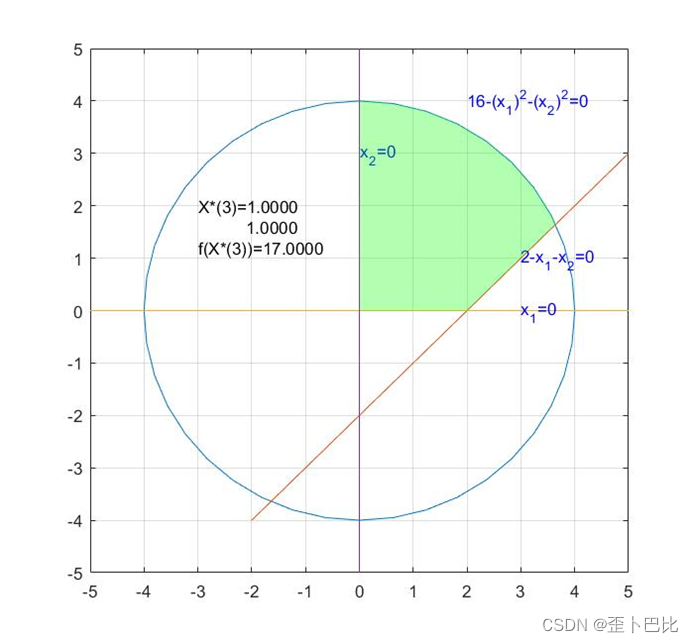
text(-3,2,'X*(3)=1.0000') 
text(-2.1,1.6,'1.0000') 
text(-3,1.2,'f(X*(3))=17.0000')