当前位置:网站首页>绕任意轴旋转矩阵推导
绕任意轴旋转矩阵推导
2022-08-03 23:34:00 【122&&113】
该文是在学习 Physically Based Rendering 第2.7.6节绕任意轴旋转时对其公式的推导产生了兴趣。
首先,如图所示: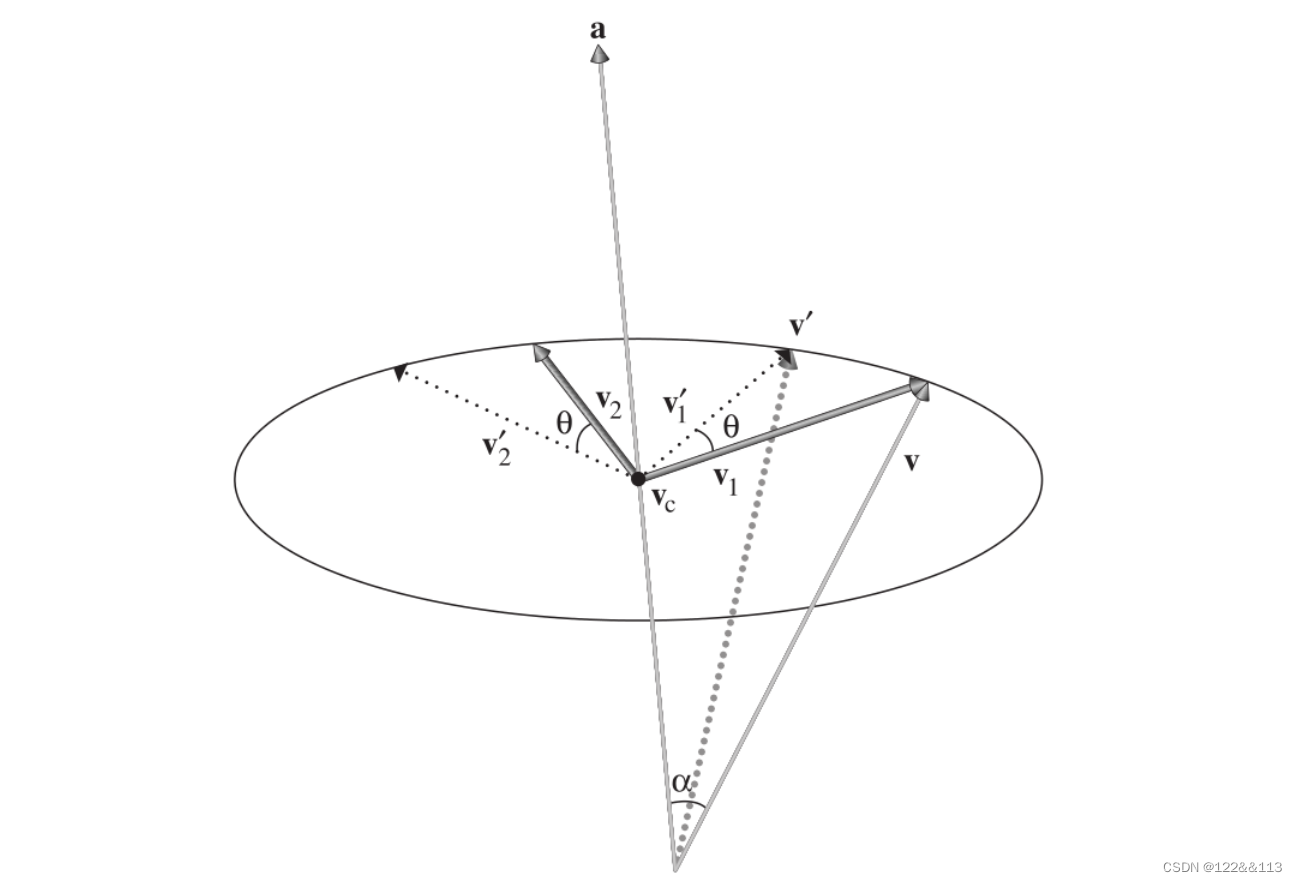
已知条件:
1). v \mathbf{v} v 是被旋转的向量。
2). a \mathbf{a} a 是围绕旋转的轴。
3). θ \theta θ 是旋转的角度。
解决思路:
通过构建坐标系 ( p , v 1 , v 2 ) (p,\mathbf{v_1},\mathbf{v_2}) (p,v1,v2) 获得绕该坐标系旋转的公式并应用到 ( 1 , 0 , 0 ) , ( 0 , 1 , 0 ) , ( 0 , 0 , 1 ) (1,0,0),(0,1,0),(0,0,1) (1,0,0),(0,1,0),(0,0,1) 的坐标系上即可获得最终应用的旋转矩阵。
假设条件:
1). a \mathbf{a} a 是单位向量,故之后用 a ^ \hat{\mathbf{a}} a^ 表示,即 ∥ a ^ ∥ = 1 \|\hat{\mathbf{a}}\|=1 ∥a^∥=1。
2). α \alpha α 为 v \mathbf{v} v 与 a ^ \hat{\mathbf{a}} a^ 的夹角。
求解:
构建向量 v 1 \mathbf{v_1} v1 ,注意全程需要结合图来理解。
v 1 = v − v c \mathbf{v_1} = \mathbf{v} - \mathbf{v_c} v1=v−vc
其中 v c = p r o j e c t ( v , a ^ ) \mathbf{v_c} = project(\mathbf{v}, \hat{\mathbf{a}}) vc=project(v,a^) ,即向量 v \mathbf{v} v 在向量 a ^ \hat{\mathbf{a}} a^ 上的投影,根据假设条件(1)和(2)可得下式:
v c = ( ∥ v ∥ cos α ) a ^ = ( ∥ v ∥ ∥ a ^ ∥ cos α ) a ^ = ( v ⋅ a ^ ) a ^ \begin{aligned} \mathbf{v_c} &= (\|\mathbf{v}\|\cos{\alpha})\hat{\mathbf{a}}\\ &= (\|\mathbf{v}\|\|\hat{\mathbf{a}}\|\cos{\alpha})\hat{\mathbf{a}} \\ &=(\mathbf{v}\cdot\hat{\mathbf{a}})\hat{\mathbf{a}} \end{aligned} vc=(∥v∥cosα)a^=(∥v∥∥a^∥cosα)a^=(v⋅a^)a^
故:
v 1 = v − ( v ⋅ a ^ ) a ^ \mathbf{v_1} = \mathbf{v} - (\mathbf{v}\cdot\hat{\mathbf{a}})\hat{\mathbf{a}} v1=v−(v⋅a^)a^由于 v c \mathbf{v_c} vc 是投影,故得到的 v 1 ⊥ a ^ \mathbf{v_1} \perp \hat{\mathbf{a}} v1⊥a^ ,因此相当于有了两个 basic vector,通过叉乘 我们可以得到第三个基向量 v 2 \mathbf{v_2} v2 ,注意这里是左手坐标系,因此因该用 v 1 × a ^ \mathbf{v_1}\times \hat{\mathbf{a}} v1×a^ 而不是 a ^ × v 1 \hat{\mathbf{a}}\times \mathbf{v_1} a^×v1,之前就是犯了这个错误,导致最后推出来的式子不对,区别可以看这篇文章:让人懵圈的左右手坐标系及Unity中的叉积
v 2 = v 1 × a ^ \mathbf{v_2} =\mathbf{v_1}\times \hat{\mathbf{a}} v2=v1×a^
这里可以通过该式获得一些隐含条件,而原书正是忽略了这些细节导致最后的公式得到的比较突然。
∥ v 2 ∥ = ∥ v 1 × a ^ ∥ ∥ v 2 ∥ = ∥ v 1 ∥ ∥ a ^ ∥ sin β \|\mathbf{v_2}\| = \|\mathbf{v_1}\times \hat{\mathbf{a}}\|\\ \|\mathbf{v_2}\| = \|\mathbf{v_1} \|\|\hat{\mathbf{a}}\|\sin{\beta} ∥v2∥=∥v1×a^∥∥v2∥=∥v1∥∥a^∥sinβ
其中如上所述, v 1 ⊥ a ^ \mathbf{v_1} \perp \hat{\mathbf{a}} v1⊥a^ ,故 β = π 2 \beta=\frac{\pi}{2} β=2π ,那么 ∥ v 2 ∥ = ∥ v 1 ∥ ∥ a ^ ∥ \|\mathbf{v_2}\| = \|\mathbf{v_1} \|\|\hat{\mathbf{a}}\| ∥v2∥=∥v1∥∥a^∥ ,又 ∥ a ^ ∥ = 1 \|\hat{\mathbf{a}}\|=1 ∥a^∥=1 ,则 ∥ v 2 ∥ = ∥ v 1 ∥ \|\mathbf{v_2}\| = \|\mathbf{v_1} \| ∥v2∥=∥v1∥现在有了三个基向量,如图,其中我们最终的目标如下:
v ′ = v c + v 1 ′ \mathbf{v'} = \mathbf{v_c}+\mathbf{v_1'} v′=vc+v1′
当前需要求解的是 v 1 ′ \mathbf{v_1'} v1′
这里也有一个隐含条件,因为向量 v \mathbf{v} v 绕 a ^ \hat{\mathbf{a}} a^ 轴旋转,且 ∥ v 2 ∥ = ∥ v 1 ∥ \|\mathbf{v_2}\| = \|\mathbf{v_1} \| ∥v2∥=∥v1∥,因此不管怎么角度怎么旋转,都在一个圆中,即 ∥ v 2 ∥ = ∥ v 1 ∥ = ∥ v 1 ′ ∥ \|\mathbf{v_2}\| = \|\mathbf{v_1} \| = \|\mathbf{v_1'}\| ∥v2∥=∥v1∥=∥v1′∥
现在来求解:
v 1 ′ = p r o j e c t ( v 1 ′ , v 1 ) + p r o j e c t ( v 1 ′ , v 2 ) = ∥ v 1 ′ ∥ cos θ v 1 ∥ v 1 ∥ + ∥ v 1 ′ ∥ sin θ v 2 ∥ v 2 ∥ = v 1 cos θ + v 2 sin θ \begin{aligned} \mathbf{v_1'} &= project(\mathbf{v_1'}, \mathbf{v_1})+project(\mathbf{v_1'}, \mathbf{v_2}) \\ &= \|\mathbf{v_1'}\|\cos{\theta}\frac{\mathbf{v_1}}{\|\mathbf{v_1}\|} + \|\mathbf{v_1'}\|\sin{\theta}\frac{\mathbf{v_2}}{\|\mathbf{v_2}\|} \\ &= \mathbf{v_1}\cos{\theta} + \mathbf{v_2}\sin{\theta} \end{aligned} v1′=project(v1′,v1)+project(v1′,v2)=∥v1′∥cosθ∥v1∥v1+∥v1′∥sinθ∥v2∥v2=v1cosθ+v2sinθ
上式中相当于把 v 1 ′ \mathbf{v_1'} v1′ 投影到两个基向量 v 1 , v 2 \mathbf{v_1, v_2} v1,v2 上,他俩相加等于 v 1 ′ \mathbf{v_1'} v1′ ,投影的时候由于 v 1 , v 2 \mathbf{v_1, v_2} v1,v2 不是单位向量,故需要归一化,又因为 ∥ v 2 ∥ = ∥ v 1 ∥ = ∥ v 1 ′ ∥ \|\mathbf{v_2}\| = \|\mathbf{v_1} \| = \|\mathbf{v_1'}\| ∥v2∥=∥v1∥=∥v1′∥ ,故消去 ∥ v 2 ∥ , ∥ v 1 ∥ , ∥ v 1 ′ ∥ \|\mathbf{v_2}\|, \|\mathbf{v_1} \| , \|\mathbf{v_1'}\| ∥v2∥,∥v1∥,∥v1′∥ 得到 v 1 ′ \mathbf{v_1'} v1′有了前面的铺垫,最终得到 v ′ \mathbf{v'} v′ 的式子:
v ′ = v c + v 1 ′ = v c + v 1 cos θ + v 2 sin θ \begin{aligned} \mathbf{v'} &= \mathbf{v_c}+\mathbf{v_1'} \\ &= \mathbf{v_c} + \mathbf{v_1}\cos{\theta} + \mathbf{v_2}\sin{\theta} \end{aligned} v′=vc+v1′=vc+v1cosθ+v2sinθ
式子推导完成后,我们需要获得旋转矩阵的一般表达。
假设 v = ( 1 , 0 , 0 ) \mathbf{v} = (1,0,0) v=(1,0,0) , a ^ = ( a x , a y , a z ) \hat{\mathbf{a}} = (a_x,a_y,a_z) a^=(ax,ay,az)
v c = ( v ⋅ a ^ ) a ^ = ( a x 2 , a x a y , a x a z ) \begin{aligned} \mathbf{v_c} &= (\mathbf{v}\cdot\hat{\mathbf{a}})\hat{\mathbf{a}} \\ &=(a_x^2,a_xa_y,a_xa_z) \end{aligned} vc=(v⋅a^)a^=(ax2,axay,axaz)
v 1 = v − ( v ⋅ a ^ ) a ^ = ( 1 − a x 2 , − a x a y , − a x a z ) \begin{aligned} \mathbf{v_1} &= \mathbf{v} - (\mathbf{v}\cdot\hat{\mathbf{a}})\hat{\mathbf{a}} \\ &=(1-a_x^2,-a_xa_y,-a_xa_z) \end{aligned} v1=v−(v⋅a^)a^=(1−ax2,−axay,−axaz)
v 2 = v 1 × a ^ = ( − a x a y a z + a x a y a z , ( 1 − a x 2 ) a z + a x 2 a z , − ( 1 − a x 2 ) a y + a x 2 a y ) = ( 0 , a z , − a y ) \begin{aligned} \mathbf{v_2} &=\mathbf{v_1}\times \hat{\mathbf{a}} \\ &=(-a_xa_ya_z+a_xa_ya_z,(1-a_x^2)a_z+a_x^2a_z,-(1-a_x^2)a_y+a_x^2a_y)\\ &= (0, a_z, -a_y) \end{aligned} v2=v1×a^=(−axayaz+axayaz,(1−ax2)az+ax2az,−(1−ax2)ay+ax2ay)=(0,az,−ay)
v ′ = v c + v 1 ′ = v c + v 1 cos θ + v 2 sin θ = ( a x 2 , a x a y , a x a z ) + ( 1 − a x 2 , − a x a y , − a x a z ) cos θ + ( 0 , a z , − a y ) sin θ = ( a x 2 + cos θ − a x 2 cos θ , a x a y − a x a y cos θ + a z sin θ , a x a z − a x a z cos θ − a y sin θ ) = [ a x 2 ( 1 − cos θ ) + cos θ , a x a y ( 1 − cos θ ) + a z sin θ , a x a z ( 1 − cos θ ) − a y sin θ ] \begin{aligned} \mathbf{v'} &= \mathbf{v_c}+\mathbf{v_1'} \\ &= \mathbf{v_c} + \mathbf{v_1}\cos{\theta} + \mathbf{v_2}\sin{\theta}\\ &= (a_x^2,a_xa_y,a_xa_z) + (1-a_x^2,-a_xa_y,-a_xa_z)\cos{\theta} + (0, a_z, -a_y)\sin{\theta} \\ &= (a_x^2 + \cos{\theta}-a_x^2\cos{\theta}, a_xa_y-a_xa_y\cos{\theta}+a_z\sin{\theta}, a_xa_z-a_xa_z\cos{\theta}-a_y\sin{\theta}) \\ &=[a_x^2(1-\cos{\theta}) + \cos{\theta}, a_xa_y(1-\cos{\theta}) +a_z\sin{\theta},a_xa_z(1-\cos{\theta}) - a_y\sin{\theta}] \end{aligned} v′=vc+v1′=vc+v1cosθ+v2sinθ=(ax2,axay,axaz)+(1−ax2,−axay,−axaz)cosθ+(0,az,−ay)sinθ=(ax2+cosθ−ax2cosθ,axay−axaycosθ+azsinθ,axaz−axazcosθ−aysinθ)=[ax2(1−cosθ)+cosθ,axay(1−cosθ)+azsinθ,axaz(1−cosθ)−aysinθ]
设置旋转矩阵为 R \mathbf{R} R ,则 R v = v ′ \mathbf{R}\mathbf{v}=\mathbf{v'} Rv=v′
即
[ x a y a z a x b y b z b x c y c z c ] [ 1 0 0 ] = [ a x 2 ( 1 − cos θ ) + cos θ a x a y ( 1 − cos θ ) + a z sin θ a x a z ( 1 − cos θ ) − a y sin θ ] \begin{bmatrix} x_a & y_a & z_a \\ x_b & y_b & z_b \\ x_c & y_c & z_c \end{bmatrix} \begin{bmatrix} 1 \\ 0 \\ 0 \end{bmatrix} = \begin{bmatrix} a_x^2(1-\cos{\theta}) + \cos{\theta} \\ a_xa_y(1-\cos{\theta}) + a_z\sin{\theta} \\ a_xa_z(1-\cos{\theta}) - a_y\sin{\theta} \end{bmatrix} ⎣⎡xaxbxcyaybyczazbzc⎦⎤⎣⎡100⎦⎤=⎣⎡ax2(1−cosθ)+cosθaxay(1−cosθ)+azsinθaxaz(1−cosθ)−aysinθ⎦⎤
通过上式可以得到旋转矩阵的第一列向量,即
R = [ x a y a z a x b y b z b x c y c z c ] = [ a x 2 ( 1 − cos θ ) + cos θ y a z a a x a y ( 1 − cos θ ) + a z sin θ y b z b a x a z ( 1 − cos θ ) − a y sin θ y c z c ] \mathbf{R}= \begin{bmatrix} x_a & y_a & z_a \\ x_b & y_b & z_b \\ x_c & y_c & z_c \end{bmatrix} =\begin{bmatrix} a_x^2(1-\cos{\theta}) + \cos{\theta} & y_a & z_a \\ a_xa_y(1-\cos{\theta}) + a_z\sin{\theta} & y_b & z_b \\ a_xa_z(1-\cos{\theta}) - a_y\sin{\theta} & y_c & z_c \end{bmatrix} R=⎣⎡xaxbxcyaybyczazbzc⎦⎤=⎣⎡ax2(1−cosθ)+cosθaxay(1−cosθ)+azsinθaxaz(1−cosθ)−aysinθyaybyczazbzc⎦⎤
同上,我们可以设 v = ( 0 , 1 , 0 ) , ( 0 , 0 , 1 ) \mathbf{v} = (0,1,0),(0,0,1) v=(0,1,0),(0,0,1) 来得到另外两个列向量的表达式。
最终的矩阵形式如下:
R = [ a x 2 ( 1 − cos θ ) + cos θ a x a y ( 1 − cos θ ) − a z sin θ a x a z ( 1 − cos θ ) + a y sin θ a x a y ( 1 − cos θ ) + a z sin θ a y 2 ( 1 − cos θ ) + cos θ a y a z ( 1 − cos θ ) − a x sin θ a x a z ( 1 − cos θ ) − a y sin θ a y a z ( 1 − cos θ ) + a x sin θ a z 2 ( 1 − cos θ ) + cos θ ] \mathbf{R} =\begin{bmatrix} a_x^2(1-\cos{\theta}) + \cos{\theta} & a_xa_y(1-\cos{\theta}) - a_z\sin{\theta} & a_xa_z(1-\cos{\theta}) + a_y\sin{\theta} \\ a_xa_y(1-\cos{\theta}) + a_z\sin{\theta} & a_y^2(1-\cos{\theta}) + \cos{\theta} & a_ya_z(1-\cos{\theta}) - a_x\sin{\theta} \\ a_xa_z(1-\cos{\theta}) - a_y\sin{\theta} & a_ya_z(1-\cos{\theta}) + a_x\sin{\theta} & a_z^2(1-\cos{\theta}) + \cos{\theta} \end{bmatrix} R=⎣⎡ax2(1−cosθ)+cosθaxay(1−cosθ)+azsinθaxaz(1−cosθ)−aysinθaxay(1−cosθ)−azsinθay2(1−cosθ)+cosθayaz(1−cosθ)+axsinθaxaz(1−cosθ)+aysinθayaz(1−cosθ)−axsinθaz2(1−cosθ)+cosθ⎦⎤
PBRT源码:
Transform Rotate(Float theta, const Vector3f &axis) {
Vector3f a = Normalize(axis);
Float sinTheta = std::sin(Radians(theta));
Float cosTheta = std::cos(Radians(theta));
Matrix4x4 m;
// Compute rotation of first basis vector
m.m[0][0] = a.x * a.x + (1 - a.x * a.x) * cosTheta;
m.m[0][1] = a.x * a.y * (1 - cosTheta) - a.z * sinTheta;
m.m[0][2] = a.x * a.z * (1 - cosTheta) + a.y * sinTheta;
m.m[0][3] = 0;
// Compute rotations of second and third basis vectors
m.m[1][0] = a.x * a.y * (1 - cosTheta) + a.z * sinTheta;
m.m[1][1] = a.y * a.y + (1 - a.y * a.y) * cosTheta;
m.m[1][2] = a.y * a.z * (1 - cosTheta) - a.x * sinTheta;
m.m[1][3] = 0;
m.m[2][0] = a.x * a.z * (1 - cosTheta) - a.y * sinTheta;
m.m[2][1] = a.y * a.z * (1 - cosTheta) + a.x * sinTheta;
m.m[2][2] = a.z * a.z + (1 - a.z * a.z) * cosTheta;
m.m[2][3] = 0;
return Transform(m, Transpose(m));
}
边栏推荐
- FinClip, help smart TV more imagination
- 【深度学习】基于tensorflow的服装图像分类训练(数据集:Fashion-MNIST)
- Software testing is seriously involution, how to improve your competitiveness?
- BMN: Boundary-Matching Network for Temporal Action Proposal Generation Reading Notes
- 用两个栈模拟队列
- BMN: Boundary-Matching Network for Temporal Action Proposal Generation阅读笔记
- redis持久化方式
- 走迷宫 BFS
- How many way of calling a function?
- 全球首款量产,获定点最多!这家AVP Tier1如何实现领跑?
猜你喜欢
直播系统聊天技术(八):vivo直播系统中IM消息模块的架构实践
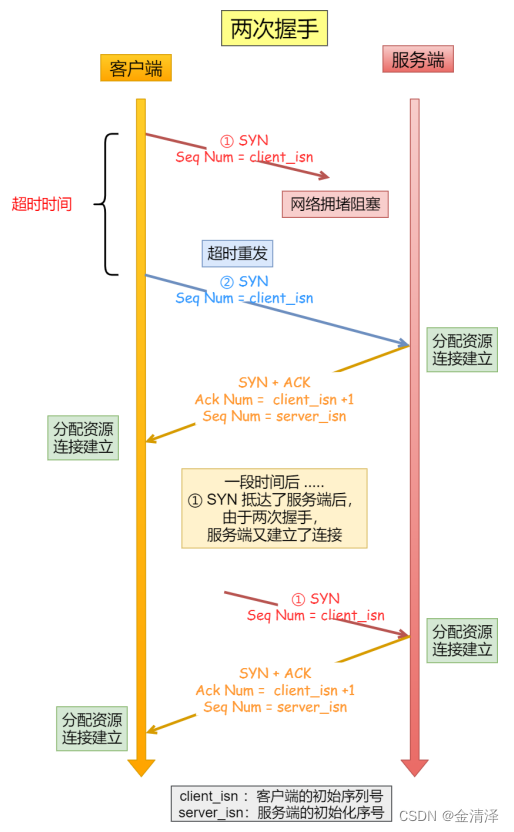
A simple understanding of TCP, learn how to shake hands, wave hands and various states
超级完美版布局有快捷键,有背景置换

Another MySQL masterpiece published by Glacier (send the book at the end of the article)!!

CAS: 178744-28-0, mPEG-DSPE, DSPE-mPEG, methoxy-polyethylene glycol-phosphatidylethanolamine supply

redis持久化方式

智能座舱的「交互设计」大战

Redis persistence method

软件测试内卷严重,如何提升自己的竞争力呢?

override learning (parent and child)
随机推荐
HNUCM 2022年暑假ACM搜索专项练习
V8中的快慢数组(附源码、图文更易理解)
Prometheus监控Harbor(二进制版)
ML之yellowbrick:基于titanic泰坦尼克是否获救二分类预测数据集利用yellowbrick对LoR逻辑回归模型实现可解释性(阈值图)案例
射频芯片(RFIC)的协议之5G及其调制
P1449 后缀表达式
汉字风格迁移---结合本地和全局特征学习的中文字体迁移
ros mavros stereo读取rosbag并记录IMU和图片到文件夹
【RYU】rest_router.py源码解析
超级完美版布局有快捷键,有背景置换
Code Casual Recording Notes_Dynamic Programming_416 Segmentation and Subsetting
创建函数报错,提示DECLARE定义语法问题
Create function report error, prompting DECLARE definition syntax problem
Flutter教程之为什么 Flutter 是创业的最佳选择?
Creo 9.0二维草图的诊断:加亮开放端点
智能座舱的「交互设计」大战
Redis persistence method
BMN: Boundary-Matching Network for Temporal Action Proposal Generation Reading Notes
Take an example of a web worker
complete binary tree problem