当前位置:网站首页>DFS对树的遍历及一些优化
DFS对树的遍历及一些优化
2022-07-29 23:07:00 【可然冫】
树的遍历
树的深度优先遍历
调用根结点 d f s ( r o o t ) dfs(root) dfs(root)
void dfs(int x)
{
vis[x]=1;
for(int i=head[x];i;i=nex[i])
{
int y=ver[i];
if(vis[y]) continue;
dfs(y);
}
}
树的DFS序
对树进行深度优先遍历时,对于每个结点,在刚进入递归后以及即将回溯时各记录一次结点编号,每个结点x在序列中恰好出现两次。
void dfs(int x)
{
a[++m]=x;
vis[x]=1;
for(int i=head[x];i;i=nex[i])
{
int y=ver[i];
if(vis[y]) continue;
dfs(y);
}
a[++m]=x;
}
树的深度
void dfs(int x)
{
vis[x]=1;
for(int i=head[x];i;i=nex[i])
{
int y=ver[i];
if(vis[y]) continue;
depth[y]=depth[x]+1;
dfs(y);
}
}
树的重心
有的时候题目不给明哪个是根结点(所有节点都可以是根结点),可以通过一次dfs找到树的重心来尽量避免“树大根深”的情况。
树的重心:设max_part(x)表示在删除结点x后产生的子树中,最大的一棵的大小。使得max_part取最小值的结点p即为树的重心。
void dfs(int x)
{
vis[x]=1;size[x]=1;//子树x的大小
int max_part=0;
for(int i=head[x];i;i=nex[i])
{
int y=ver[i];
if(vis[y]) continue;
dfs(y);
size[x]+=size[y];
max_part=max(max_part,size[y]);//找最大子树
}
max_part=max(max_part,n-size[x]);
if(max_part<ans)
{
ans=max_part;//记录重心对应的最大子树规模
pos=x;//记录重心
}
}
2018HBCPC的一道题: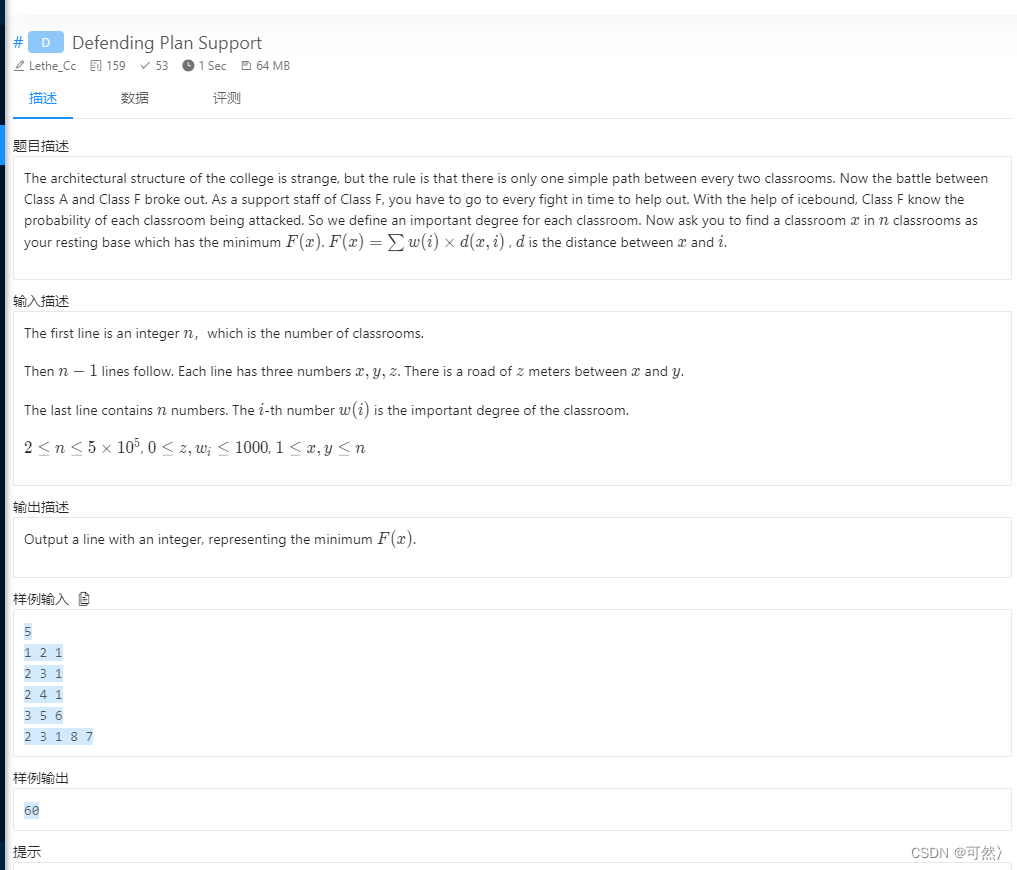
找到一个点x,使得 F ( x ) = ∑ w ( i ) ∗ d ( x , i ) F(x)=\sum{w(i)}*d(x,i) F(x)=∑w(i)∗d(x,i)最小,w(i)是结点i的权值,d(x,i)是d到i的距离。
#include<bits/stdc++.h>
#define llg long long
#define inf 0x3ffffff
using namespace std;
const int N=1e6+10;
int head[N],ver[N],nex[N],val[N],tot,n,dis[N],vis[N];
int size[N],pos,max_size,ans=inf;
long long minn=1e15;
inline int read()
{
int x=0,f=1;char ch=getchar();
while (ch<'0'||ch>'9'){
if (ch=='-') f=-1;ch=getchar();}
while (ch>='0'&&ch<='9'){
x=x*10+ch-48;ch=getchar();}
return x*f;
}
void add(int x,int y,int z)
{
ver[++tot]=y,dis[tot]=z,nex[tot]=head[x],head[x]=tot;
}
void dfs1(int x)
{
vis[x]=1,size[x]=1;
int max_size=0;
for(int i=head[x];i;i=nex[i])
{
if(vis[ver[i]]) continue;
vis[ver[i]]=1;
dfs1(ver[i]);
size[x]+=size[ver[i]];
max_size=max(max_size,size[ver[i]]);
}
max_size=max(max_size,n-size[x]);
if(max_size<ans)
{
ans=max_size;
pos=x;
}
}
long long dfs(int x,int d)
{
//cout<<"x:"<<x<<" d:"<<d<<endl;
vis[x]=1;
long long sum=0;
for(int i=head[x];i;i=nex[i])
{
if(vis[ver[i]]) continue;
vis[ver[i]]=1;
sum+=val[ver[i]]*(dis[i]+d);
sum+=dfs(ver[i],dis[i]+d);
}
return sum;
}
int main()
{
n=read();
for(int i=1;i<n;i++)
{
int x=read(),y=read(),z=read();
add(x,y,z);
add(y,x,z);
}
for(int i=1;i<=n;i++)
val[i]=read();
dfs1(1);//找重心
//cout<<"pos:"<<pos<<endl;
memset(vis,0,sizeof(vis));
cout<<dfs(pos,0);
return 0;
}
连通块划分
void dfs(int x)
{
v[x]=cnt;
int max_part=0;
for(int i=head[x];i;i=nex[i])
{
int y=ver[i];
if(vis[y]) continue;
dfs(y);
}
}
int main()
{
for(int i=1;i<=n;i++)
{
if(!v[i])
{
cnt++;
dfs(i);
}
}
}
剪枝
- 优化搜索顺序
- 排除冗余信息
- 可行性剪枝(照当前分支这样走后面不可能达成)
- 最优性剪枝(照当前分支这样走的最优解都比当前解差)
- 记忆化搜索
#include<bits/stdc++.h>
using namespace std;
int n,w,c[20],a[20],cnt,ans;
void dfs(int num,int cnt)
{
if(cnt>=ans) return;//最优性剪枝
if(num==n+1)//n只喵都塞进去了
{
ans=min(ans,cnt);
return;
}
for(int i=1;i<=cnt;i++)
{
if(w-a[i]>=c[num])
{
a[i]+=c[num];
dfs(num+1,cnt);
a[i]-=c[num];
}
}
a[cnt+1]=c[num];
dfs(num+1,cnt+1);
a[cnt+1]=0;
}
int main()
{
cin>>n>>w;
ans=n;
for(int i=1;i<=n;i++)
cin>>c[i];
sort(c+1,c+n+1);
reverse(c+1,c+n+1);//优化搜索顺序,重的喵放在前面
dfs(1,0);
cout<<ans;
return 0;
}
主要考虑优化搜索顺序,从可选的数少的空格开始试探。所以我们在每次搜索时都判断一下哪个格子的可选到数最小。
#include<bits/stdc++.h>
using namespace std;
const int N=9;
string str;
int mp[1<<N],nums[1<<N],row[N],col[N],cell[N][N];
inline int lowbit(int x)
{
return x&(-x);
}
int get(int x,int y)
{
return row[x]&col[y]&cell[x/3][y/3];//求出这一个位置可能会被填哪些数字
}
void init()//初始化:所有位所有数字都可以填
{
for(int i=0;i<N;i++)
row[i]=col[i]=(1<<N)-1;
for(int i=0;i<3;i++)
for(int j=0;j<3;j++)
cell[i][j]=(1<<N)-1;
}
bool dfs(int cnt)
{
if(cnt==0) return true;//所有待填数字都已经被填上
int minn=10,x,y;
for(int i=0;i<N;i++)
for(int j=0;j<N;j++)
{
if(str[i*9+j]=='.')
{
int temp=nums[get(i,j)];
if(temp<minn)
{
minn=temp;
x=i,y=j;
}
}
}//找到所有剩下的待填格中数字集合最小的一个,是一个剪枝过程
for(int i=get(x,y);i;i-=lowbit(i))//枚举这一格所有可能填的数字
{
int t=mp[lowbit(i)];
row[x]-=(1<<t);
col[y]-=(1<<t);
cell[x/3][y/3]-=(1<<t);
str[x*9+y]='1'+t;
if(dfs(cnt-1)) return true;
row[x]+=(1<<t);
col[y]+=(1<<t);
cell[x/3][y/3]+=(1<<t);
str[x*9+y]='.';//复原
}
return false;
}
int main()
{
for(int i=0;i<N;i++) mp[1<<i]=i;//预先存下二进制1所在的位置
for(int i=1;i<(1<<N);i++)
for(int j=i;j;j-=lowbit(j)) nums[i]++;
//预先存下每个之后可能会枚举到的二进制数内有几个1
while(cin>>str&&str[0]!='e')
{
init();
int cnt=0;
for(int i=0,k=0;i<9;i++)
for(int j=0;j<9;j++,k++)
{
if(str[k]!='.')
{
int t=str[k]-'1';//1~9映射到0~8
row[i]-=(1<<t);
col[j]-=(1<<t);
cell[i/3][j/3]-=(1<<t);
}//这一位数字是题给的,把它存进对应位置
else cnt++;//待填数字+1
}
dfs(cnt);
cout<<str<<endl;
}
return 0;
}
#include<bits/stdc++.h>
using namespace std;
int n,a[70],sum,maxn,len,cnt,v[70];
bool dfs(int stick,int cab,int last)
//正在拼第stick根木棒(stick-1)根已拼好
//第stick根木棒的当前长度为cab
//拼接到第stivk根木棒中的上一根小木棍为last
{
if(stick>cnt) return true;//所有木棒都拼好
if(cab==len) return dfs(stick+1,0,1);//第stick个拼好
int fail=0;
for(int i=last;i<=n;i++)//木棍长度递减(从last开始枚举)
{
if(!v[i]&&cab+a[i]<=len&&fail!=a[i])
//排除冗余:之前搜过这么长的木棍,已经fail过了,就不要一fail再fail了
{
v[i]=1;
if(dfs(stick,cab+a[i],i+1)) return true;
fail=a[i];
v[i]=0;
if(cab==0||cab+a[i]==len)
return false;
//cab==0,尝试拼入第一根木棍就失败,没必要往后继续了,因为长度为0的木棍都是等效的,怎么拼都是失败
//can+a[i]==len这一整根能拼好,但是后面还是不能完全拼好,没必要在这里往更短的试了
}
}
return false;
}
int main()
{
cin>>n;
for(int i=1;i<=n;i++)
{
cin>>a[i];
sum+=a[i];
maxn=max(maxn,a[i]);
}
sort(a+1,a+n+1);
reverse(a+1,a+n+1);//优化搜索顺序,优先尝试较长的木棍
for(len=maxn;len<=sum;len++)
{
if(sum%len) continue;
cnt=sum/len;//原始木棒长度为len,共有cnt根
//cout<<"len:"<<len<<" cnt:"<<cnt<<endl;
memset(v,0,sizeof(v));
if(dfs(1,0,1))
{
cout<<len;
break;
}
}
}
建议直接看视频,躺
#include<bits/stdc++.h>
using namespace std;
#define inf 1e9
int n,m,minv[25],mins[25];
int R[25],H[25],ans=inf;
void dfs(int u,int v,int s)
// 当前层数,已用体积,已用面积
{
if(v+minv[u]>n) return;//可行性剪枝
if(s+mins[u]>=ans) return;//最优性剪枝
if(s+2*(n-v)/R[u+1]>=ans) return;//最优性剪枝
if(!u)
{
if(v==n) ans=s;
return;
}
for(int i=min((int)sqrt(n-v),R[u+1]-1);i>=u;i--)//上下界剪枝
{
for(int j=min((n-v)/(i*i),H[u+1]-1);j>=u;j--)//上下界剪枝
{
H[u]=j,R[u]=i;
int t=(u==m?i*i:0);
dfs(u-1,v+i*i*j,s+2*i*j+t);
}
}
}
int main()
{
cin>>n>>m;
for(int i=1;i<=m;i++)
{
minv[i]=minv[i-1]+i*i*i;
mins[i]=mins[i-1]*2*i*i;
}
R[m+1]=H[m+1]=inf;
dfs(m,0,0);
if(ans==inf) ans=0;
cout<<ans;
return 0;
}
记忆化搜索
#include<bits/stdc++.h>
using namespace std;
int a[105][105],mem[105][105],ans;
int dx[4]={
1,0,-1,0};
int dy[4]={
0,1,0,-1};
int R,C;
int dfs(int x,int y)
{
if(mem[x][y]) return mem[x][y];
mem[x][y]=1;
for(int i=0;i<4;i++)
{
int xx=x+dx[i];
int yy=y+dy[i];
if(a[xx][yy]<a[x][y]&&xx>0&&yy>0&&xx<=R&&yy<=C)
{
dfs(xx,yy);
mem[x][y]=max(mem[x][y],1+mem[xx][yy]);
}
}
return mem[x][y];
}
int main()
{
cin>>R>>C;
for(int i=1;i<=R;i++)
for(int j=1;j<=C;j++)
scanf("%d",&a[i][j]);
for(int i=1;i<=R;i++)
for(int j=1;j<=C;j++)
ans=max(ans,dfs(i,j));
cout<<ans;
return 0;
}
迭代加深
搜索树规模随着层次的深入增长很快,并且能够确保答案在一个较浅层的结点内——>限制搜索深度,每次在该深度内找不到答案就返回,增加一单位深度后再搜索。这会导致重复搜索浅层,但这比起庞大的子树来微不足道。比如是二叉树, 1 + 2 + 2 2 + 2 3 + . . . + 2 d e p t h − 1 < 2 d e p t h 1+2+2^{2}+2^{3}+...+2^{depth-1}<2^{depth} 1+2+22+23+...+2depth−1<2depth
#include<bits/stdc++.h>
using namespace std;
const int N=10010;
int path[N],st[N],n;
bool dfs(int u,int depth)
{
if(u==depth) return path[u-1]==n;//最后一个数是n即找到答案
bool st[N]={
0};
for(int i=u-1;i>=0;i--)
for(int j=i;j>=0;j--)//优化搜索顺序,i和j从大到小枚举
{
int temp=path[i]+path[j];
if(!st[temp]&&temp<=n&&path[u-1]<temp)
//!st[temp]剪枝,因为有多种可能的 temp=path[i]+path[j],但是只需要搜索一次
//这个数一定<=n且比前一层的数大
{
path[u]=temp;
st[temp]=1;
if(dfs(u+1,depth)) return true;
}
}
return false;
}
int main()
{
path[0]=1;
while(cin>>n,n)
{
int depth=1;
while(!dfs(1,depth)) depth++;//迭代加深的过程
for(int i=0;i<depth;i++)
cout<<path[i]<<' ';
cout<<endl;
}
return 0;
}
双向搜索
从初态和终态出发各搜索一半状态,产生两棵深度减半的搜索树,在中间交会、组合成最终的答案。
把礼物分成前一半,后一半,对于前一半,就暴搜,记录每次搜索完成后的总重量;对于后一半,也暴搜,每次搜索完成后与前一半合并。怎么合并?在前一半二分出一个重量,这个重量和后一半暴搜完的重量加起来不超过w而且尽可能大。用ans记录最大的一个合并总重。
#include<bits/stdc++.h>
#define llg long long
#define inf 0x3ffffff
using namespace std;
const int N=46;
llg weight[1<<24],ans,g[N],w,n,k,cnt,tot;
void dfs1(int v,int s)
{
if(v==k)
{
weight[cnt++]=s;
return;
}
if((llg)s+g[v]<=w) dfs1(v+1,s+g[v]);//选
dfs1(v+1,s);//不选
}
void dfs2(int v,int s)
{
if(v==n)
{
llg l=0,r=tot-1;
while(l<r)
{
llg mid=(l+r+1)>>1;
if(weight[mid]+(llg)s<=w) l=mid;
else r=mid-1;
}
ans=max(ans,s+weight[l]);
return;
}
if((llg)s+g[v]<=w) dfs2(v+1,s+g[v]);//选
dfs2(v+1,s);//不选
}
int main()
{
cin>>w>>n;
for(int i=0;i<n;i++)
scanf("%lld",&g[i]);
sort(g,g+n);
reverse(g,g+n);
k=n/2;
dfs1(0,0);
sort(weight,weight+cnt);
tot=unique(weight,weight+cnt)-weight;
dfs2(k,0);
cout<<ans;
}
边栏推荐
- MySQL active/standby switch
- Override and customize dependent native Bean methods
- BGP联邦综合实验
- 【2023校招刷题】常见面试问题总结(七、常见总线协议篇)(随后续面试不断更新....)
- 【leetcode】剑指 Offer II 006. 排序数组中两个数字之和(二分查找、双指针)
- y81.第四章 Prometheus大厂监控体系及实战 -- 监控扩展(十二)
- JetsonNano learning (6) Big pits and solutions that Jetson stepped on___Continuously updated
- The latest Gansu construction welder (construction special operation) simulation question bank and answer analysis in 2022
- HRNet-Facial-Landmark-Detection 训练自己数据集
- 云计算1+X之openstack篇
猜你喜欢

C语言实现扫雷(9*9)游戏——详解

DNA脱氧核糖核酸修饰四氧化三铁|DNA修饰氧化锌|使用方法

437. 路径总和 III ●●

Topics in Dynamic Programming

华为14天-(3)内核开发

DNA偶联二维过渡金属硫化物|DNA修饰贵金属纳米颗粒|使用方法

Guidelines for the Release of New WeChat Mini Programs

Raspberry pie wiringPi 2.6 installed on solving gpio readall command mistakes

【无标题】

【leetcode】82. 删除排序链表中的重复元素 II(中等)
随机推荐
【leetcode】80. 删除有序数组中的重复项 II(中等)(双指针、原地修改)
NetWorker Knowledge Corner|Easy to get an offer [Networker Interview Questions] What is the difference between a Layer 3 switch and a router?
This article penetrates the architecture design and cluster construction of the distributed storage system Ceph (hands-on)
超分之RVRT
嵌入式系统驱动初级【1】——内核模块上_编译方法
【无标题】清空吗
[C] list explanation (headless ChanXiangFei cycle)
树莓派上安装 wiringPi 2.6 解决 gpio readall 命令的错误
使用 Neuron 接入 Modbus TCP 及 Modbus RTU 协议设备
Guidelines for the Release of New WeChat Mini Programs
The Sandbox Partners with Gravity to Bring RO Ragnarok to the Metaverse
Topics in Dynamic Programming
J9 Number Theory: Why do we need Web3?
推荐 7 个学习 Web3 的开源资源
The second round of the real offer harvester~ How does the big factory inspect the candidates?(with detailed answer)
地狱挖掘者系列#1
高数下|三重积分习题课|高数叔|手写笔记
bgp基础配置和宣告
【leetcode】50. Pow(x, n)(中等)(快速幂)
WeChat applet sliding navigation bar (how to set the floating window of the webpage)