当前位置：网站首页>Topics in Dynamic Programming
Topics in Dynamic Programming
2022-07-29 22:48:00 【51CTO】
动态规划
文章目录
- 动态规划
- 一,最大/最小问题
- 1.1 [使用最小花费爬楼梯](https://leetcode-cn.com/problems/min-cost-climbing-stairs/)
- 1.2 [最小路径和](https://leetcode-cn.com/problems/minimum-path-sum/)
- 1.3 [零钱兑换](https://leetcode-cn.com/problems/coin-change/)
- 1.4 [下降路径最小和](https://leetcode-cn.com/problems/minimum-falling-path-sum/)
- 1.5 [最低票价](https://leetcode-cn.com/problems/minimum-cost-for-tickets/)
- 1.6 [只有两个键的键盘](https://leetcode-cn.com/problems/2-keys-keyboard/)
- 1.6 [完全平方数](https://leetcode-cn.com/problems/perfect-squares/)
- 1.7 [加油站](https://leetcode-cn.com/problems/gas-station/)
- 1.8 [最大正方形](https://leetcode-cn.com/problems/maximal-square/)
- 二,背包问题
- 2.1 [最后一块石头的重量 II](https://leetcode-cn.com/problems/last-stone-weight-ii/)
- 2.2 [一和零](https://leetcode-cn.com/problems/ones-and-zeroes/)
- 3.1 [爬楼梯](https://leetcode-cn.com/problems/climbing-stairs/)
- 3.2[不同路径](https://leetcode-cn.com/problems/unique-paths/)
- 3.3[不同路径 II](https://leetcode-cn.com/problems/unique-paths-ii/)
- 3.4[目标和](https://leetcode-cn.com/problems/target-sum/)
- 3.5 [“马”在棋盘上的概率](https://leetcode-cn.com/problems/knight-probability-in-chessboard/)
- 3.6[组合总和 Ⅳ](https://leetcode-cn.com/problems/combination-sum-iv/)
- 3.7[最长上升子序列](https://leetcode-cn.com/problems/longest-increasing-subsequence/)
- 3.8[最长递增子序列的个数](https://leetcode-cn.com/problems/number-of-longest-increasing-subsequence/)
- 四,区间合并
- 4.1[叶值的最小代价生成树](https://leetcode-cn.com/problems/minimum-cost-tree-from-leaf-values/)
- 4.2[不同的二叉搜索树](https://leetcode-cn.com/problems/unique-binary-search-trees/)
- 五,序列问题
- 5.1[最长公共子序列](https://leetcode-cn.com/problems/longest-common-subsequence/)
- 5.2[回文子串](https://leetcode-cn.com/problems/palindromic-substrings/)
- 5.3[最长回文子串](https://leetcode-cn.com/problems/longest-palindromic-substring/)
- 5.4[最长回文子序列](https://leetcode-cn.com/problems/longest-palindromic-subsequence/)
- 5.5[编辑距离](https://leetcode-cn.com/problems/edit-distance/)
- 6.1[打家劫舍](https://leetcode-cn.com/problems/house-robber/)
- 6.2[打家劫舍 II](https://leetcode-cn.com/problems/house-robber-ii/)
- 6.3[打家劫舍 III](https://leetcode-cn.com/problems/house-robber-iii/)
一,最大/最小问题
模板：
1.1 使用最小花费爬楼梯
状态定义：
The idea of recursive equation derivation：
- Can span level：dp[i - 1]
- Across two level：dp[i - 2]
- 那么dp[i]Can be the first across two levelsi级,It can also be a step up,所以：
- dp[i] = Min(dp[i - 1],dp[i - 2]) + cost[i]
- 注意,第array.length级台阶是第array.length - 1top of steps,So if you want to get on, you need to step over.,Put it as a cost0virtual stairs
- dp[i] = Min(dp[i - 1],dp[i - 2]) + (i == array.length ? 0 : cost[i])
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
初始状态处理：
实现：
public
int
minCostClimbingStairs(
int[]
cost) {
if(
cost.
length
==
0){
return
0;
}
if(
cost.
length
==
1){
return
cost[
0];
}
if(
cost.
length
==
2){
return
Math.
min(
cost[
0],
cost[
1]);
}
int
n
=
cost.
length;
int[]
dp
=
new
int[
n
+
1];
dp[
0]
=
cost[
0];
dp[
1]
=
cost[
1];
for(
int
i
=
2;
i
<=
n;
i
++){
dp[
i]
=
Math.
min(
dp[
i
-
1],
dp[
i
-
2])
+ (
i
==
n
?
0 :
cost[
i]);
}
return
dp[
n];
}
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
- 15.
- 16.
- 17.
- 18.
- 19.
1.2 最小路径和
状态定义：
初始状态：
状态方程：
实现：
public
int
minPathSum(
int[][]
grid) {
if(
grid.
length
==
0){
return
0;
}
int
m
=
grid.
length;
int
n
=
grid[
0].
length;
int[][]
dp
=
new
int[
m
+
1][
n
+
1];
dp[
0][
0]
=
grid[
0][
0];
// 只有一列
for(
int
i
=
1;
i
<
m;
i
++){
dp[
i][
0]
=
dp[
i
-
1][
0]
+
grid[
i][
0];
}
// 只有一行
for(
int
i
=
1;
i
<
n;
i
++){
dp[
0][
i]
=
dp[
0][
i
-
1]
+
grid[
0][
i];
}
for(
int
i
=
1;
i
<=
m;
i
++){
for(
int
j
=
1;
j
<=
n;
j
++){
dp[
i][
j]
=
Math.
min(
dp[
i
-
1][
j],
dp[
i][
j
-
1])
+
grid[
i][
j];
}
}
return
dp[
m][
n];
}
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
- 15.
- 16.
- 17.
- 18.
- 19.
- 20.
- 21.
- 22.
- 23.
1.3 零钱兑换
状态定义：
状态方程：
实现：
public
int
coinChange(
int[]
coins,
int
amount) {
int[]
dp
=
new
int[
amount
+
1];
Arrays.
fill(
dp,
amount
+
1);
dp[
0]
=
0;
for(
int
i
=
1;
i
<=
amount;
i
++){
for(
int
j
=
0;
j
<
coins.
length;
j
++){
if(
i
>=
coins[
j]){
dp[
i]
=
Math.
min(
dp[
i],
dp[
i
-
coins[
j]]
+
1);
}
}
}
return
dp[
amount]
>
amount
?
-
1 :
dp[
amount];
}
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
1.4 下降路径最小和
状态定义：
状态方程：
实现：
public
int
minFallingPathSum1(
int[][]
A) {
// 设dp[i][j]为到i, j位置的最小路径和
int
len
=
A.
length;
int[][]
dp
=
new
int[
len
+
1][
len
+
2];
for (
int
i
=
0;
i
<
len
+
1;
i
++) {
dp[
i][
0]
=
Integer.
MAX_VALUE;
dp[
i][
len
+
1]
=
Integer.
MAX_VALUE;
}
for (
int
j
=
0;
j
<
len
+
2;
j
++) {
dp[
0][
j]
=
0;
}
int
ans
=
Integer.
MAX_VALUE;
for (
int
i
=
1;
i
<
len
+
1;
i
++) {
for (
int
j
=
1;
j
<
len
+
1;
j
++) {
dp[
i][
j]
=
Math.
min(
Math.
min(
dp[
i
-
1][
j
-
1],
dp[
i
-
1][
j]),
dp[
i
-
1][
j
+
1])
+
A[
i
-
1][
j
-
1];
}
}
for (
int
i
=
1;
i
<
len
+
1;
i
++) {
ans
=
Math.
min(
ans,
dp[
len][
i]);
}
return
ans;
}
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
- 15.
- 16.
- 17.
- 18.
- 19.
- 20.
- 21.
- 22.
- 23.
- 24.
1.5 最低票价
状态定义：
状态方程：
实现：
public
int
mincostTickets(
int[]
days,
int[]
costs) {
// 第nday to travel： dp[ n ]=min( dp[ n-1 ] + cost[ 0 ] , dp[ n-7 ] + cost[ 1 ] , dp[ n-30 ] + cost[ 2 ] )
// 第ndays do not travel：dp[n] = dp[n - 1]
int[]
dp
=
new
int[
396];
// day数组下标
int
index
=
0;
for(
int
i
=
31;
index
<
days.
length
&&
i
<=
395;
i
++){
if(
days[
index]
!=
i
-
30){
// 第ino need to travel
dp[
i]
=
dp[
i
-
1];
continue;
}
index
++;
dp[
i]
=
Math.
min(
dp[
i
-
1]
+
costs[
0],
Math.
min(
dp[
i
-
7]
+
costs[
1],
dp[
i
-
30]
+
costs[
2]));
}
return
dp[
days[
days.
length
-
1]
+
30];
}
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
- 15.
- 16.
- 17.
1.6 只有两个键的键盘
状态定义：
状态方程：
实现：
public
int
minSteps(
int
n) {
int[]
dp
=
new
int[
n
+
1];
// dp[i]：得到icharacters require at least a few steps
int
h
= (
int)
Math.
sqrt(
n);
for (
int
i
=
2;
i
<=
n;
i
++) {
dp[
i]
=
i;
for (
int
j
=
2;
j
<=
h;
j
++) {
// 质数：dp[i],得到i个字符最少需要i步操作
if (
i
%
j
==
0) {
// 合数：dp[i]：将iNumber of operations to decompose to the prime factors that cannot be decomposed
dp[
i]
=
dp[
j]
+
dp[
i
/
j];
break;
}
}
}
return
dp[
n];
}
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
- 15.
- 16.
- 17.
1.6 完全平方数
状态定义：
状态转移方程：
实现：
public
int
numSquares(
int
n) {
if(
n
<
2){
return
n;
}
int[]
dp
=
new
int[
n
+
1];
// dp[i]：找到dp[i]perfect squares such that their sum=i;
for(
int
i
=
0;
i
<=
n;
i
++){
dp[
i]
=
i;
}
for(
int
i
=
2;
i
<=
n;
i
++){
for(
int
j
=
1;
j
*
j
<=
i;
j
++){
dp[
i]
=
Math.
min(
dp[
i],
dp[
i
-
j
*
j]
+
1) ;
}
}
return
dp[
n];
}
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
- 15.
- 16.
1.7 加油站
思路：
过程分析：
cur：Mainly used to analyze whether you can go to the next subscript,If not immediatelycur < 0,then you need to update the starting subscript,At the same time anew from the cylinder oil0开始：
rest：Traverse once to calculate the overallgasSum - costSum,如果rest <= 0Definitely can't go all the way around
- 1.
- 2.
- 3.
实现：
public
int
canCompleteCircuit(
int[]
gas,
int[]
cost) {
int
cur
=
0;
int
start
=
0;
int
rest
=
0;
for(
int
i
=
0;
i
<
gas.
length;
i
++){
cur
+= (
gas[
i]
-
cost[
i]);
rest
+= (
gas[
i]
-
cost[
i]);
if(
cur
<
0){
cur
=
0;
start
=
i
+
1;
}
}
return
rest
>=
0
?
start :
-
1;
}
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
1.8 最大正方形
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-9Uw5BS4D-1610893042600)(C:%5CUsers%5C12642%5CAppData%5CRoaming%5CTypora%5Ctypora-user-images%5Cimage-20200719223554043.png)]
状态：
状态方程：
以（3,3）The square in the lower right corner may contain three squares
实现：
public
int
maximalSquare(
char[][]
matrix) {
// dp(i,j) 表示以 (i, j)(i,j) 为右下角,且只包含 11 的正方形的边长最大值
// dp[i][j] = min(dp[i-1][j],dp[i-1][j-1],dp[i][j-1]) + 1
if(
matrix.
length
==
0
||
matrix[
0].
length
==
0){
return
0;
}
int
maxSide
=
0;
int[][]
dp
=
new
int[
matrix.
length][
matrix[
0].
length];
for(
int
i
=
0;
i
<
matrix.
length;
i
++){
for(
int
j
=
0;
j
<
matrix[
0].
length;
j
++){
if(
matrix[
i][
j]
==
'1') {
if (
i
==
0
||
j
==
0) {
dp[
i][
j]
=
1;
}
else{
dp[
i][
j]
=
Math.
min(
dp[
i
-
1][
j],
Math.
min(
dp[
i
-
1][
j
-
1],
dp[
i][
j
-
1]))
+
1;
}
}
maxSide
=
Math.
max(
maxSide,
dp[
i][
j]);
}
}
return (
int)
Math.
pow(
maxSide,
2);
}
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
- 15.
- 16.
- 17.
- 18.
- 19.
- 20.
- 21.
- 22.
二,背包问题
2.1 最后一块石头的重量 II
2.2 一和零
三,How many ways to solve a problem
3.1 爬楼梯
状态定义：
状态方程：
实现：
3.2 不同路径
状态定义：
状态方程：
实现：
public
int
uniquePaths(
int
m,
int
n) {
int[][]
dp
=
new
int[
m][
n];
for(
int
i
=
0;
i
<
m;
i
++){
dp[
i][
0]
=
1;
}
for(
int
i
=
0;
i
<
n;
i
++){
dp[
0][
i]
=
1;
}
for(
int
i
=
1;
i
<
m;
i
++){
for(
int
j
=
1;
j
<
n;
j
++){
dp[
i][
j]
=
dp[
i
-
1][
j]
+
dp[
i][
j
-
1];
}
}
return
dp[
m
-
1][
n
-
1];
}
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
- 15.
3.3 不同路径 II
状态定义：
状态方程：
实现：
public
int
uniquePathsWithObstacles(
int[][]
obstacleGrid) {
int
m
=
obstacleGrid.
length;
int
n
=
obstacleGrid[
0].
length;
int[][]
dp
=
new
int[
m][
n];
// Note that entry and exit may be obstructed
for(
int
i
=
0;
i
<
m
&&
obstacleGrid[
i][
0]
==
0;
i
++){
dp[
i][
0]
=
1;
}
for(
int
i
=
0;
i
<
n
&&
obstacleGrid[
0][
i]
==
0;
i
++){
dp[
0][
i]
=
1;
}
for(
int
i
=
1;
i
<
m;
i
++){
for(
int
j
=
1;
j
<
n;
j
++){
if(
obstacleGrid[
i][
j]
!=
1){
dp[
i][
j]
=
dp[
i
-
1][
j]
+
dp[
i][
j
-
1];
}
else{
dp[
i][
j]
=
0;
}
}
}
return
dp[
m
-
1][
n
-
1];
}
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
- 15.
- 16.
- 17.
- 18.
- 19.
- 20.
- 21.
- 22.
3.4 目标和
状态定义：
状态方程：
实现：
public
int
findTargetSumWays(
int[]
nums,
int
S) {
int
sum
=
0;
for (
int
num :
nums) {
sum
+=
num;
}
if (
sum
<
S
|| (
sum
+
S)
%
2
==
1) {
return
0;
}
int
w
= (
sum
+
S)
/
2;
int[]
dp
=
new
int[
w
+
1];
dp[
0]
=
1;
for (
int
num :
nums) {
for (
int
j
=
w;
j
>=
num;
j
--) {
dp[
j]
+=
dp[
j
-
num];
}
}
return
dp[
w];
}
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
- 15.
- 16.
- 17.
- 18.
3.5 “马”在棋盘上的概率
状态定义：
状态方程：
实现：
public
double
knightProbability(
int
N,
int
K,
int
r,
int
c) {
// 在第r,clocation passeskProbability of staying on the board after a move
int[][]
dir
= {{
-
2,
-
1}, {
-
2,
1}, {
-
1,
2}, {
1,
2}, {
2,
1}, {
2,
-
1}, {
1,
-
2}, {
-
1,
-
2}};
double[][][]
dp
=
new
double[
N][
N][
K
+
1];
for (
int
i
=
0;
i
<
N;
i
++) {
for (
int
j
=
0;
j
<
N;
j
++) {
dp[
i][
j][
0]
=
1;
}
}
for (
int
k
=
1;
k
<=
K;
k
++) {
for (
int
i
=
0;
i
<
N;
i
++) {
for (
int
j
=
0;
j
<
N;
j
++) {
for (
int
d
=
0;
d
<
dir.
length;
d
++) {
int
nx
=
i
+
dir[
d][
0];
int
ny
=
j
+
dir[
d][
1];
if (
nx
>=
0
&&
nx
<
N
&&
ny
>=
0
&&
ny
<
N) {
dp[
i][
j][
k]
+= (
dp[
nx][
ny][
k
-
1])
/
8;
}
}
//提前返回
if (
i
==
r
&&
j
==
c
&&
k
==
K) {
return
dp[
i][
j][
k];
}
}
}
}
return
dp[
r][
c][
K];
}
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
- 15.
- 16.
- 17.
- 18.
- 19.
- 20.
- 21.
- 22.
- 23.
- 24.
- 25.
- 26.
- 27.
- 28.
3.6 组合总和 Ⅳ
状态定义：
状态方程：
实现：
3.7 最长上升子序列
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-AvHMQEbX-1610893042603)(C:%5CUsers%5C12642%5CAppData%5CRoaming%5CTypora%5Ctypora-user-images%5Cimage-20200726135123464.png)]
状态定义：
状态方程：
实现：
public
int
lengthOfLIS(
int[]
nums) {
if(
nums.
length
<=
0){
return
0;
}
// 当数组长度为i时,上升子序列的最长长度
int[]
dp
=
new
int[
nums.
length
+
1];
// A number itself is also a subsequence
Arrays.
fill(
dp,
1);
for(
int
i
=
1;
i
<
nums.
length;
i
++){
for(
int
j
=
0;
j
<
i;
j
++){
if(
nums[
i]
>
nums[
j]){
dp[
i]
=
Math.
max(
dp[
i],
dp[
j]
+
1);
}
}
}
int
res
=
dp[
0];
for (
int
i
=
0;
i
<
nums.
length;
i
++) {
res
=
Math.
max(
res,
dp[
i]);
}
return
res;
}
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
- 15.
- 16.
- 17.
- 18.
- 19.
- 20.
- 21.
3.8 最长递增子序列的个数
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-honl71tv-1610893042605)(C:%5CUsers%5C12642%5CAppData%5CRoaming%5CTypora%5Ctypora-user-images%5Cimage-20200726141337385.png)]
状态定义：
实现：
public
int
findNumberOfLIS(
int[]
nums) {
if (
nums.
length
==
0) {
return
0;
}
int[]
dp
=
new
int[
nums.
length];
int[]
combination
=
new
int[
nums.
length];
Arrays.
fill(
dp,
1);
Arrays.
fill(
combination,
1);
int
max
=
1,
res
=
0;
for (
int
i
=
1;
i
<
dp.
length;
i
++) {
for (
int
j
=
0;
j
<
i;
j
++) {
if (
nums[
i]
>
nums[
j]) {
if (
dp[
j]
+
1
>
dp[
i]) {
//如果+1长于当前LIS 则组合数不变
dp[
i]
=
dp[
j]
+
1;
combination[
i]
=
combination[
j];
}
else
if (
dp[
j]
+
1
==
dp[
i]) {
//如果+1等于当前LIS 则说明找到了新组合
combination[
i]
+=
combination[
j];
}
}
}
max
=
Math.
max(
max,
dp[
i]);
}
for (
int
i
=
0;
i
<
nums.
length;
i
++)
if (
dp[
i]
==
max)
res
+=
combination[
i];
return
res;
}
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
- 15.
- 16.
- 17.
- 18.
- 19.
- 20.
- 21.
- 22.
- 23.
- 24.
- 25.
- 26.
- 27.
- 28.
四,区间合并
4.1 叶值的最小代价生成树
状态定义：
状态方程：
实现：
public
int
mctFromLeafValues(
int[]
arr) {
// 从i到j最小和 = kThe product of the maximum value of the elements on the left and right sides of the node + 子问题k左边（i到k）最小值 * 子问题（k+1到j）最小值
int
n
=
arr.
length;
if(
n
==
0
||
n
==
1){
return
0;
}
// dp[i][j]：从i到j的最小和
int[][]
dp
=
new
int[
n][
n];
for(
int
d
=
1;
d
<
n;
++
d){
for(
int
i
=
0;
i
+
d
<
n;
++
i){
dp[
i][
i
+
d]
=
Integer.
MAX_VALUE;
for(
int
k
=
i;
k
<
i
+
d;
++
k){
dp[
i][
i
+
d]
=
Math.
min(
dp[
i][
i
+
d],
dp[
i][
k]
+
dp[
k
+
1][
i
+
d]
+
max(
arr,
i,
k)
*
max(
arr,
k
+
1,
i
+
d));
}
}
}
return
dp[
0][
n
-
1];
}
private
int
max(
int[]
arr,
int
begin,
int
end){
int
ans
=
0;
for(
int
i
=
begin;
i
<=
end;
i
++){
ans
=
Math.
max(
ans,
arr[
i]);
}
return
ans;
}
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
- 15.
- 16.
- 17.
- 18.
- 19.
- 20.
- 21.
- 22.
- 23.
- 24.
- 25.
- 26.
4.2 不同的二叉搜索树
状态定义：
状态方程：
实现：
public
int
numTrees(
int
n) {
//return dfs(1,n);
// 以nnodes to constructBST,How many can be constructedBST
int[]
dp
=
new
int[
n
+
1];
dp[
0]
=
1;
// An empty tree is also a tree
dp[
1]
=
1;
// A node constructs a tree
for(
int
i
=
2;
i
<=
n;
i
++){
for(
int
j
=
0;
j
<
i;
j
++){
// dp[i] = dp[i-1] * dp[n-i-1]
dp[
i]
+=
dp[
j]
*
dp[
i
-
j
-
1];
}
}
return
dp[
n];
}
private
int
dfs(
int
start,
int
end) {
if(
start
>
end){
return
1;
}
// 以iis the number of left and right subtrees of the root node
int
sum
=
0;
for(
int
i
=
start;
i
<=
end;
i
++){
int
left
=
dfs(
start,
i
-
1);
// 以（i-1）-（start）construct the left subtree
int
right
=
dfs(
i
+
1,
end);
// 以（end）-（i+1）construct the right subtree
sum
+=
left
*
right;
// 构建笛卡尔积
}
return
sum;
}
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
- 15.
- 16.
- 17.
- 18.
- 19.
- 20.
- 21.
- 22.
- 23.
- 24.
- 25.
- 26.
- 27.
- 28.
五,序列问题
5.1 最长公共子序列
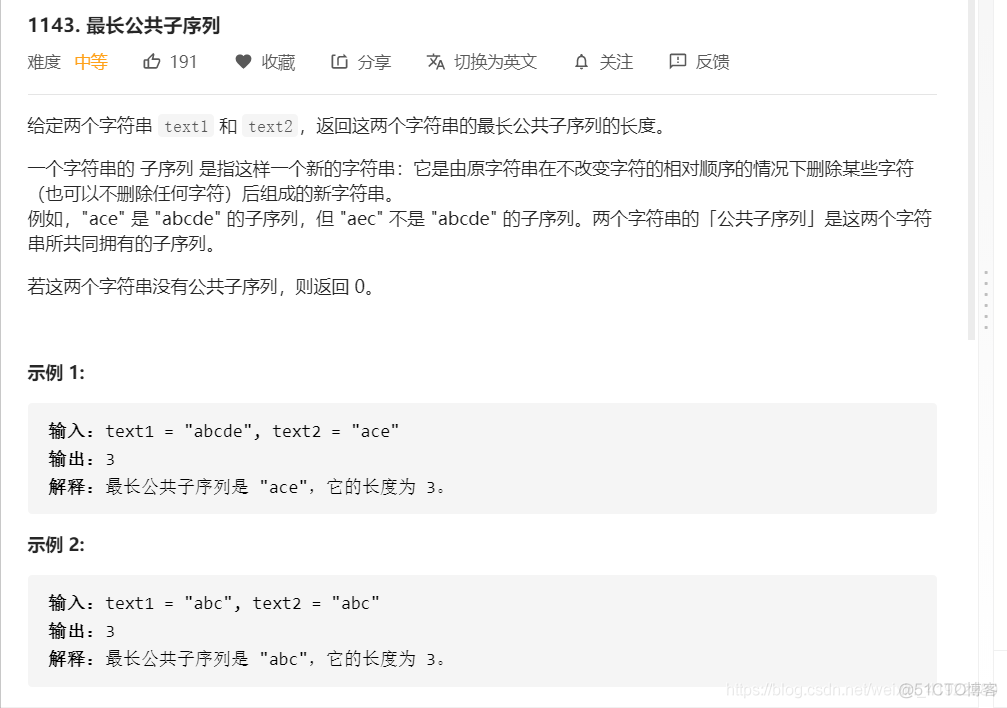
状态定义：
状态方程：
实现：
public
int
longestCommonSubsequence(
String
text1,
String
text2) {
// text1和text2的最长公共子序列长度
int[][]
dp
=
new
int[
text1.
length()
+
1][
text2.
length()
+
1];
// 初始化
for(
int
i
=
0;
i
<
text1.
length();
i
++){
dp[
i][
0]
=
0;
}
for(
int
i
=
0;
i
<
text2.
length();
i
++){
dp[
0][
i]
=
0;
}
for(
int
i
=
1;
i
<=
text1.
length();
i
++){
for(
int
j
=
1;
j
<=
text2.
length();
j
++){
if(
text1.
charAt(
i
-
1)
==
text2.
charAt(
j
-
1)){
dp[
i][
j]
=
dp[
i
-
1][
j
-
1]
+
1;
}
else{
// 如果不等的话,要么text1移动一位,要么text2移动一位
dp[
i][
j]
=
Math.
max(
dp[
i
-
1][
j],
dp[
i][
j
-
1]);
}
}
}
return
dp[
text1.
length()][
text2.
length()];
}
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
- 15.
- 16.
- 17.
- 18.
- 19.
- 20.
- 21.
- 22.
5.2 回文子串
状态定义：
状态方程：
实现：
public
int
countSubstrings(
String
s) {
// dp[i]：对于长度为i的字符串,回文子串的数量
boolean[][]
dp
=
new
boolean[
s.
length()
+
1][
s.
length()
+
1];
// 初始化,Each character is a palindrome substring
int
res
=
0;
int
n
=
s.
length();
char[]
charArr
=
s.
toCharArray();
for (
int
i
=
n
-
1;
i
>=
0;
i
--) {
for (
int
j
=
i;
j
<
n;
j
++) {
//j-i = {0,1,2}代表一个,两个,三个,字符时 此时可以根据charArr[i] == charArr[j]
//得到s[i..j]must palindrome
if (
charArr[
i]
==
charArr[
j]
&& (
j
-
i
<=
2
||
dp[
i
+
1][
j
-
1])) {
dp[
i][
j]
=
true;
res
++;
}
}
}
return
res;
}
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
- 15.
- 16.
- 17.
- 18.
- 19.
5.3 最长回文子串
状态定义：
状态方程：
实现：
public
String
longestPalindrome(
String
s) {
String
res
=
"";
int
len
=
0;
boolean[][]
dp
=
new
boolean[
s.
length()
+
1][
s.
length()
+
1];
for(
int
i
=
s.
length()
-
1;
i
>=
0;
i
--){
for(
int
j
=
i;
j
<
s.
length();
j
++){
if(
s.
charAt(
i)
==
s.
charAt(
j)
&& (
j
-
i
<=
2
||
dp[
i
+
1][
j
-
1])) {
dp[
i][
j]
=
true;
if (
j
-
i
+
1
>
len) {
len
=
Math.
max(
len,
j
-
i
+
1);
res
=
s.
substring(
i,
j
+
1);
}
}
else{
dp[
i][
j]
=
false;
}
}
}
return
res;
}
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
- 15.
- 16.
- 17.
- 18.
- 19.
5.4 最长回文子序列
状态定义：
状态方程：
实现：
public
int
longestPalindromeSubseq(
String
s) {
int
n
=
s.
length();
// f[i][j] 表示 s 的第 i 个字符到第 j 个字符组成的子串中,最长的回文序列长度是多少.
int[][]
f
=
new
int[
n][
n];
for (
int
i
=
n
-
1;
i
>=
0;
i
--) {
f[
i][
i]
=
1;
for (
int
j
=
i
+
1;
j
<
n;
j
++) {
if (
s.
charAt(
i)
==
s.
charAt(
j)) {
f[
i][
j]
=
f[
i
+
1][
j
-
1]
+
2;
}
else {
f[
i][
j]
=
Math.
max(
f[
i
+
1][
j],
f[
i][
j
-
1]);
}
}
}
return
f[
0][
n
-
1];
}
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
- 15.
- 16.
5.5 编辑距离
状态定义：
状态方程：
实现：
public
int
minDistance(
String
word1,
String
word2) {
int[][]
dp
=
new
int[
word1.
length()
+
1][
word2.
length()
+
1];
for(
int
i
=
0;
i
<=
word1.
length();
i
++){
dp[
i][
0]
=
i;
}
for(
int
i
=
0;
i
<=
word2.
length();
i
++){
dp[
0][
i]
=
i;
}
for(
int
i
=
1;
i
<=
word1.
length();
i
++){
for(
int
j
=
1;
j
<=
word2.
length();
j
++){
if (
word1.
charAt(
i
-
1)
==
word2.
charAt(
j
-
1)) {
dp[
i][
j]
=
dp[
i
-
1][
j
-
1];
}
else {
dp[
i][
j]
=
1
+
Math.
min(
Math.
min(
dp[
i
-
1][
j],
dp[
i][
j
-
1]),
dp[
i
-
1][
j
-
1]);
} }
}
return
dp[
word1.
length()][
word2.
length()];
}
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
- 15.
- 16.
- 17.
- 18.
六,decide the problem
6.1 打家劫舍
状态定义：
实现：
public
int
rob(
int[]
nums) {
if(
nums.
length
==
0){
return
0;
}
if(
nums.
length
==
1){
return
nums[
0];
}
int[]
dp
=
new
int[
nums.
length];
dp[
0]
=
nums[
0];
dp[
1]
=
Math.
max(
nums[
0],
nums[
1]);
for(
int
i
=
2;
i
<
nums.
length;
i
++){
dp[
i]
=
Math.
max(
dp[
i
-
1],
dp[
i
-
2]
+
nums[
i]);
}
return
dp[
nums.
length
-
1];
}
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
- 15.
6.2 打家劫舍 II
状态：
实现：
public
int
rob(
int[]
nums) {
if(
nums.
length
==
0)
return
0;
if(
nums.
length
==
1)
return
nums[
0];
return
Math.
max(
tryRob(
Arrays.
copyOfRange(
nums,
0,
nums.
length
-
1)),
tryRob(
Arrays.
copyOfRange(
nums,
1,
nums.
length)));
}
public
int
tryRob(
int[]
nums) {
if(
nums.
length
==
0){
return
0;
}
int[]
dp
=
new
int[
nums.
length
+
1];
dp[
0]
=
0;
dp[
1]
=
nums[
0];
for(
int
i
=
2;
i
<=
nums.
length;
i
++){
//状态转移方程：dp[i] = max{dp[i-1],dp[i-2]+nums[i-1]}
dp[
i]
=
Math.
max(
dp[
i
-
1],
dp[
i
-
2]
+
nums[
i
-
1]);
}
return
dp[
nums.
length];
}
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
- 15.
- 16.
- 17.
- 18.
- 19.
- 20.
- 21.
6.3 打家劫舍 III
递归实现：
public
int
rob(
TreeNode
root) {
return
tryRob(
root);
}
/**
* 以rootReturns the maximum value stolen for the root node
* @param root
* @return
*/
private
int
tryRob(
TreeNode
root){
if(
root
==
null){
return
0;
}
// 偷取root节点
int
res
=
0;
res
+=
root.
val;
if(
root.
left
!=
null){
res
+=
tryRob(
root.
left.
left)
+
tryRob(
root.
left.
right);
}
if(
root.
right
!=
null){
res
+=
tryRob(
root.
right.
left)
+
tryRob(
root.
right.
right);
}
// 不偷root节点
int
resWithoutRoot
=
tryRob(
root.
left)
+
tryRob(
root.
right);
return
Math.
max(
resWithoutRoot,
res);
}
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
- 15.
- 16.
- 17.
- 18.
- 19.
- 20.
- 21.
- 22.
- 23.
- 24.
- 25.
- 26.
边栏推荐
- 支持keep alive长连接【转】
- 将文件流转成file文件后使用luckysheet回显数据
- 趣味隐写术与密码术(现代密码学教程)
- Add a logo to the upper left corner of the picture, add time and address to the lower left corner, and wrap the line when the address reaches the specified length
- 高等数学（第七版）同济大学 习题3-8 个人解答
- OR63 删除公共字符
- [Point Cloud] M3DeTR: Multi-representation, Multi-scale, Mutual-relation 3D Object Detection with Transformers
- 【板栗糖GIS】arcmap—如何快捷替换属性表中的部分内容
- Sorry, it's hard for you to earn middle-aged money
- SAP MIGO 报错-在例程WERT_SIMULIEREN字段NEUER_PREIS中字段溢出
猜你喜欢
随机推荐
新库上线 | CnOpenData租赁和商务服务业工商注册企业基本信息数据
Spark读取多目录
程序员「小镇做题」出身，月薪是父母半年收入 ……
GBASE 8s 如何并行执行update statistics
【移动应用开发】2022/2023 年 8 大移动应用程序开发趋势
leetcode 890. Find and Replace Pattern（查找和替换pattern)
怎样下载国内外专利？
Xshell 7 prompts "To continue using this program, you must apply the latest update or use a new version"
JZ23 链表中环的入口结点
GBASE 8s 数据库的大对象和日志备份
外文论文的格式规范要求有哪些？
【CVPR2022】A Unified Query-based Paradigm for Point Cloud Understanding
Numpy array processing (2)
十一、HikariCP源码分析之HouseKeeper
03-树3 Tree Traversals Again（树的遍历）
中科院TextMind(文心)安装及使用
【板栗糖GIS】arcmap—标注太长，如何换行显示
【板栗糖GIS】wps—如何查看表格中的超链接
GBASE 8s 如何查看 sbspace 中的可用空间
tkinter绘制组件（31）——支点标题