当前位置:网站首页>【[USACO12MAR]Cows in a Skyscraper G】【状压DP && DFS】
【[USACO12MAR]Cows in a Skyscraper G】【状压DP && DFS】
2022-08-02 15:28:00 【Eternity_GQM】
文章目录
[USACO12MAR]Cows in a Skyscraper G
题目描述
关于 Bessie 和朋友的一个鲜为人知的事实是,他们喜欢爬楼梯比赛。 一个更广为人知的事实是奶牛真的不喜欢下楼梯。 所以在奶牛们跑到他们最喜欢的摩天大楼的顶部之后,他们遇到了一个问题。 拒绝使用楼梯爬下来,奶牛被迫使用电梯回到底层。
电梯的最大承重能力为 W (1 <= W <= 100,000,000) 磅,奶牛 i 的重量为 C_i (1 <= C_i <= W) 磅。 请帮助 Bessie 弄清楚如何使用最少的电梯次数将所有 N (1 <= N <= 18) 头奶牛送到一楼。 每次乘坐电梯时奶牛的重量总和不得大于 W。
给出n个物品,体积为w[i],现把其分成若干组,要求每组总体积<=W,问最小分组。(n<=18)
输入格式
* 第 1 行:N 和 W 用空格分隔。
* 第 2…1+N 行:第 i+1 行包含整数 C_i,给出其中一头奶牛的重量。
输出格式
* 一个整数 R,表示所需的最少乘梯次数。
样例 #1
样例输入 #1
4 10
5
6
3
7
样例输出 #1
3
提示
有四头奶牛,体重分别为 5、6、3 和 7 磅。 电梯的最大承重能力为 10 磅。
我们可以将重 3 的母牛与其他任何母牛放在同一个电梯上,但其他三头母牛太重而无法组合。 对于上述解决方案,乘坐电梯 1 涉及奶牛 #1 和 #3,乘坐电梯 2 涉及奶牛 #2,乘坐电梯 3 涉及奶牛 #4。 对于这个输入,其他几种解决方案也是可能的。
解题思路
给出n个物品,体积为w[i],现把其分成若干组,要求每组总体积<=W,问最小分组。(n<=18)
dp[i][j]表示已经开了i架电梯,j是二进制数
dp[i][j]的值表示当前电梯里的重量。
dp[i][j]初始化
只有一头牛的电梯的重量就是 dp[1][k] = w[i]
其中 k 为二进制只有一位为1的十进制数。
例如:
000001 表示 1 第一只牛
000010 表示 2 第二只牛
000100 表示 4 第三只牛
001000 表示 8 第四只牛
memset(dp, inf, sizeof(dp));
for (int i = 0; i < n; i++)
dp[1][1 << i] = w[i];
代码解析
状态压缩解法:
//给出n个物品,体积为w[i],现把其分成若干组
//要求每组总体积<=W,问最小分组。(n<=18)
int dp[20][1 << 18];
//dp[i][j]表示已经开了i架电梯,j是二进制数
//dp[i][j]的值表示当前电梯里的重量。
int n, m, w[20];
void solve(){
cin >> n >> m;
for (int i = 0; i < n; i++)
cin >> w[i];
memset(dp, inf, sizeof(dp));
for (int i = 0; i < n; i++)
dp[1][1 << i] = w[i];
for (int i = 0; i <= n; i++){
for (int j = 0; j < (1 << n);j++){
if(dp[i][j]!=inf){
for (int k = 0; k < n; k++){
if(j&(1<<k))//已经在电梯上
// 1 & 1 = 1
continue;
if(dp[i][j]+w[k]<=m){
//这个牛可以挤进去
// 1 | 0 = 1
// 0 | 1 = 1
// 0 | 0 = 0
dp[i][j | (1 << k)] = min(dp[i][j | (1 << k)], dp[i][j] + w[k]);
}else{
//i+1 电梯数+1 新的电梯就只装了一头牛w[k]
dp[i + 1][j | (1 << k)] = min(dp[i][j | (1 << k)], w[k]);
}
}
}
}
}
for (int i = 0; i <= n;i++){
if (dp[i][(1 << n) - 1] != inf){
//第一个被更新的方案数就是最少方案数
cout << i;
break;
}
}
}
DFS解法:
int n, m;
int w[20]; //每头牛的重量
int resize[20]; //电梯的剩余重量
int tot; //tot是用来记录有多少挤到已经有物品的箱子里的物品个数
int ans; //ans最优答案
void dfs(int x,int cnt){
if (x == n + 1){
//搜索到最后一头牛
ans = min(ans, cnt);//更新答案
return;
}
if (cnt >= ans)//当前方案已经大于当前最优方案,剪枝
return;
for (int i = 1; i <= x - tot;i++){
//枚举箱子,看物品x是否能放入那个箱子
//由于不可能有体积大于容量的物品,所以第x个物品顶多会用到第x个箱子,
//假如说原本每个物品都独占一个箱子,
//因为有的物品和别的物品共用一个箱子,这必然会腾出该物品原来占有的箱子,
//所以只需枚举到x-tot个箱子就可以了。
if (resize[i] < w[x])//剩余重量<当前牛的重量
continue;
if (resize[i] == m)
cnt++; //盒子数++
else
tot++; //挤到别的盒子里
resize[i] -= w[x]; //剩余容量减去
dfs(x + 1, cnt); //下一只牛
resize[i] += w[x]; //回溯
if(resize[i] == m)
cnt--;
else
tot--;
}
}
void solve(){
cin >> n >> m;
for (int i = 1; i <= n;i++)
cin >> w[i], resize[i] = m;
int ans = inf;
dfs(1, 0);
cout << ans << nl;
}
边栏推荐
猜你喜欢
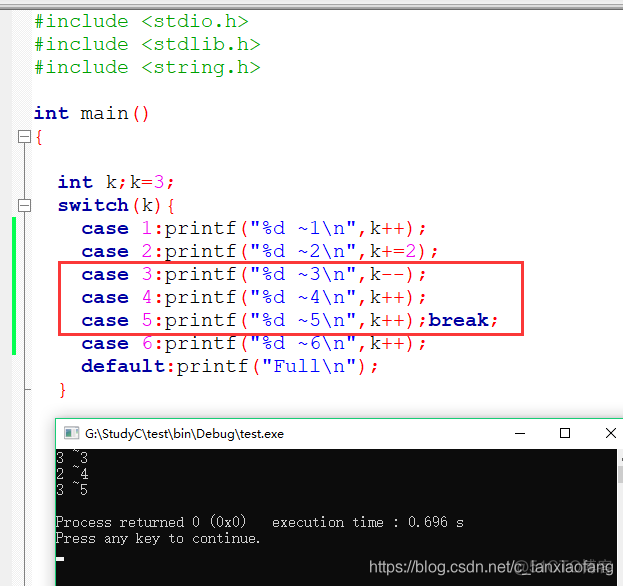
入门关于 switch case 的理解
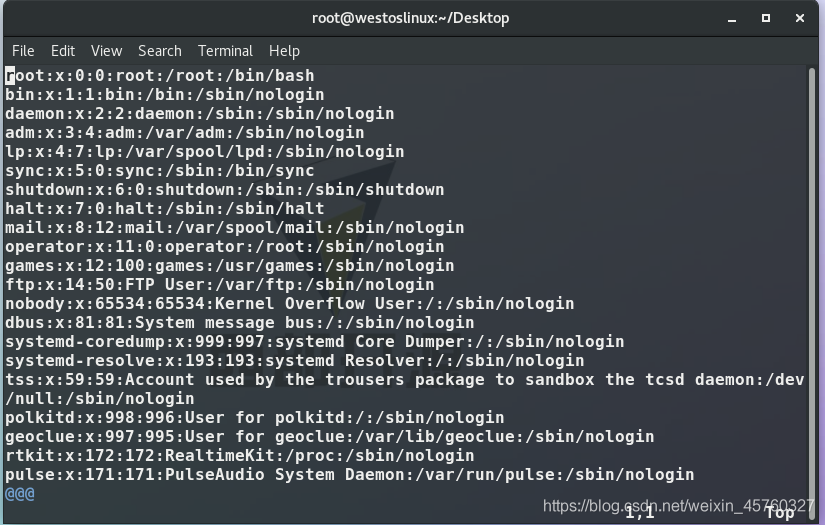
Advanced usage of vim configuration

已经2022下半年了,居然还在说链动2+1!
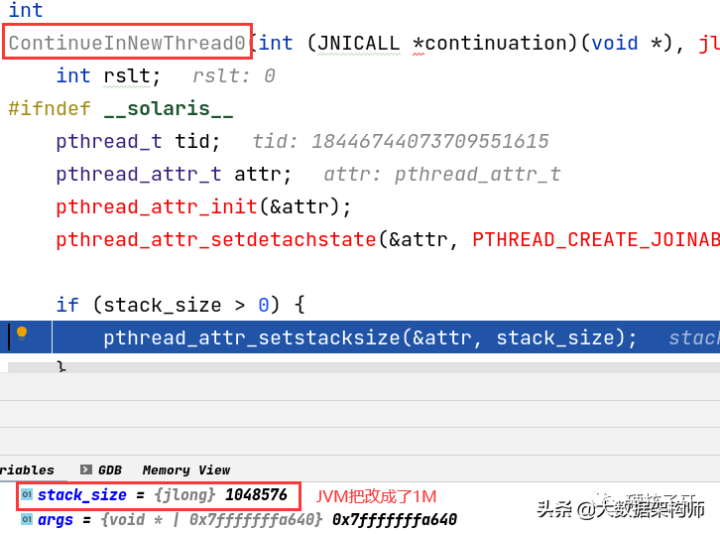
Brute-force cracking of the latest JVM interview questions of Meituan: unlimited execution

【服务器数据恢复】Raid阵列更换故障硬盘后数据同步失败的数据恢复案例
SQL实现将多行记录合并成一行
打破千篇一律,DIY属于自己独一无二的商城
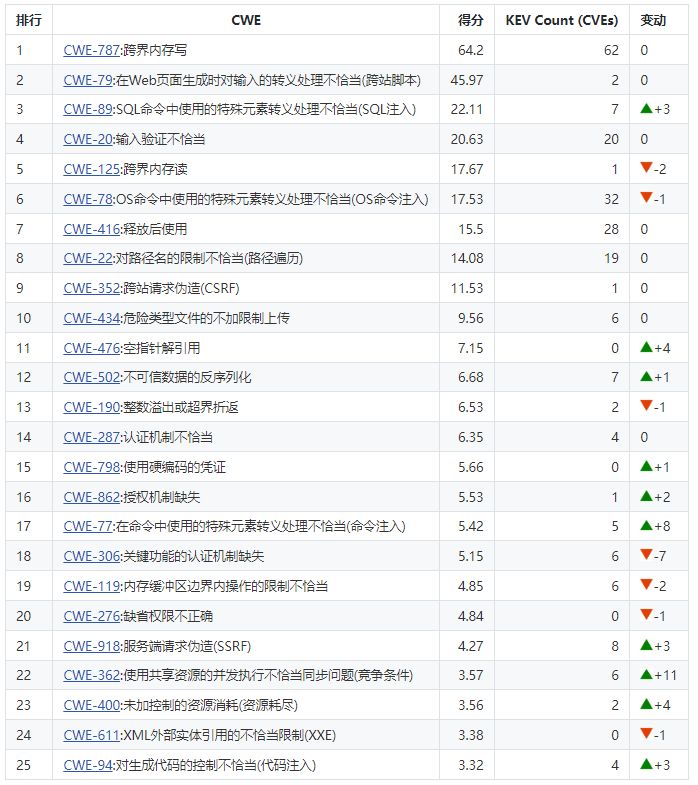
CWE4.8:2022年危害最大的25种软件安全问题

高并发 MySQL 性能优化指南,自取

Linux系统中mysql数据库的基本管理
随机推荐
看我如何用多线程,帮助运营小姐姐解决数据校对系统变慢!
不平衡之钥: 重采样法何其多
浅聊组合函数
Azure Kinect(K4A)人体识别跟踪进阶
.NET性能优化-使用SourceGenerator-Logger记录日志
RecSys'22 推荐系统论文梳理
2.3 - P、V、S机制
Apache management and web optimization
ICML/ICLR'22 推荐系统论文梳理
MySQL-1-环境部署
莫比乌斯反演学习笔记
【个人总结】2022.7月结
SQL学习笔记——REGEXP运算符
VPP snort插件
不平衡问题: 深度神经网络训练之殇
SQL查询数据以及排序
tiup mirror modify
SIGIR'22 推荐系统论文之序列推荐(长文)篇
Go-5-简单介绍fmt库
轻松入门自然语言处理系列 专题8 源码解读──基于HMM的结巴分词