Sum of four squares, laser bombs

四平方和(简单）

Three layers of brute force traversal,Then square the last number to find out whether it satisfies the requirement of a positive integer,There is a data timeout

#include <iostream>
#include <stdio.h>
#include <cmath>
using namespace std;

const int N = 5e6;
int n;
int a[N];
int main(){
    
    int a,b,c,d;
    scanf("%d",&n);
    for(int a = 0;a*a <= n;a++)
        for(int b = a;a*a+b*b <= n;b++)
            for(int c = b;a*a+b*b+c*c<= n;c++)
                {
    
                    int t = n - a*a-b*b-c*c;
                    int d = sqrt(t);
                    if(d*d==t) //如果tCan be expressed as the sum of squares of a positive integer
                    {
    
                        printf("%d %d %d %d",a,b,c,d);
                        return 0; 
                    }
                }
    return 0;
}

1、使用哈希表记录c dtwo records,c*c+d*das a subscript of the hash table,存储对应的c和d,And only one group will be saved and it will be the first groupc*c+d*d
2、将从0到n的cdThe combinations are preserved,再遍历0到n的ab组合,验证是否满足 n - a*a - b*b

#include<bits/stdc++.h>
using namespace std;

const int N = 1e5;
typedef pair<int,int> pii;

unordered_map<int,pii> mp;

int main(){
    
    int n;
    scanf("%d",&n);
    for(int c = 0;c*c <= n;c++)
        for(int d = c; c*c+d*d <= n;d++)
            {
       
                int t = c*c+d*d;
                if(mp.count(t) == 0)  mp[t] = {
    c,d};
            }
            
    for(int a = 0;a*a <= n;a++)
        for(int b = a;a*a+b*b <= n;b++)
        {
    
            int k = n - a*a - b*b;
            if(mp.count(k)) 
            {
    
                printf("%d %d %d %d",a,b,mp[k].first,mp[k].second);
                return 0;
            }
        }
        return 0 ;
}

但是仍然超时

最后AC的代码 In fact, the same principle as above 使用哈希表 但是不算c++内置的 哈希表 There is no timeout…

#include<iostream>
#include<cmath>
using namespace std;
const int N = 1e8 + 10;
int h[N];
int main() {
    
    int n;
    cin >> n;
    //打表,找出1 - n,The sum of all perfect squares,If it exists, only the first occurrence is recorded（The question asks to find the lexicographically small）
    for (int i = 0; i * i * 2<= n; i++) {
    
        for (int j = i; j * j + i * i <= n; j++) {
    
            if (!h[i * i + j * j])
                h[i * i + j * j] = i + 1;//防止i = 0When judging the search to skip later i = 0的情况
        }
    }
    //0<= a <= b <= c <= d,可以得出a^2 <= n / 4, a^2 + b^ 2 <= n / 2; 
    for (int i = 0; i * i * 4 <= n; i++) {
    
        for (int j = i; j * j + i * i <= n / 2; j++) {
    
            int t = n - i * i - j * j;
            if (h[t]) {
    
                int c = h[t] - 1;   
                //After the root sign is prevented, it is because of the precision,向下取整,例:25 The root number is obtained4.99999向下取整为4;
                int d = (sqrt(t - c * c) + 1e-4);
                printf("%d %d %d %d", i, j, c, d);
                return 0;
            }
        }
    }
    return 0;
}

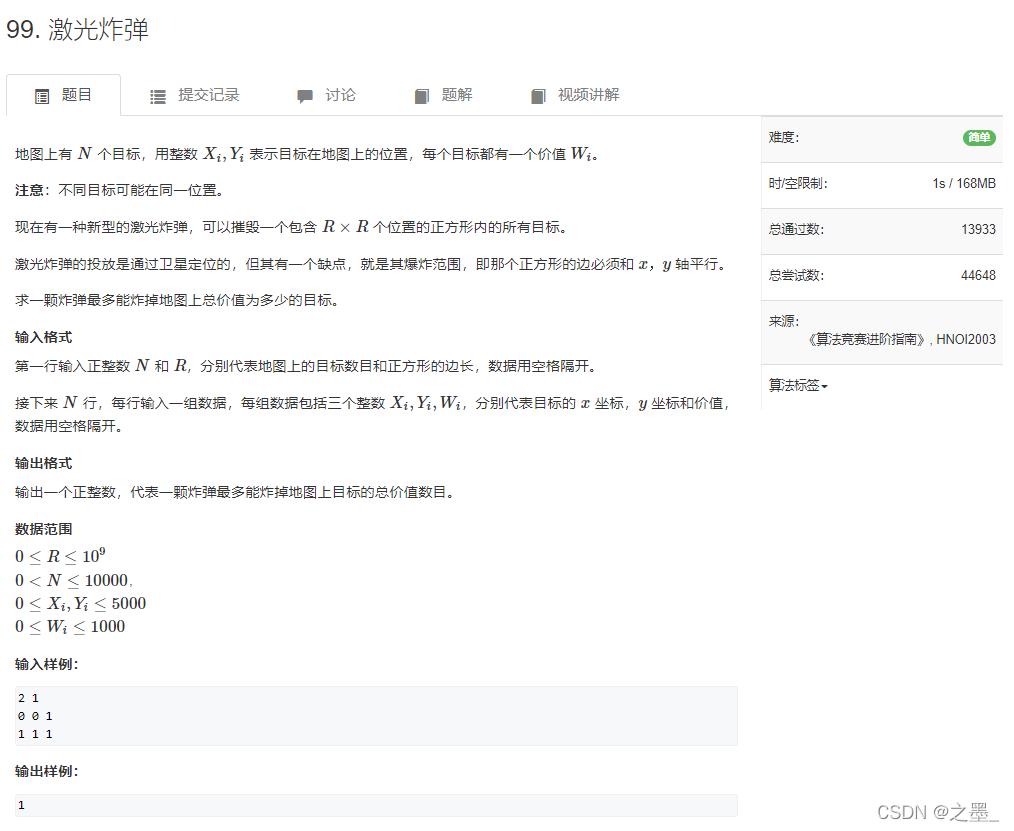
激光炸弹(简单)

The dots on the side don't count,This case is four points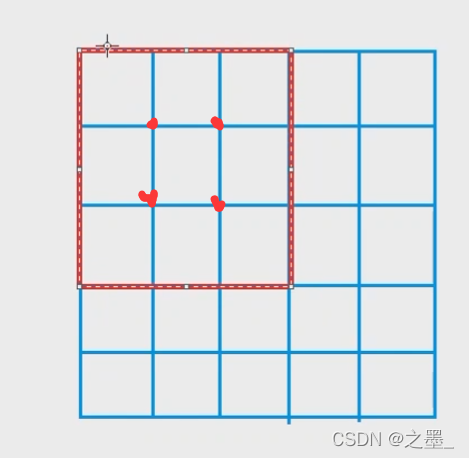

这样有9个点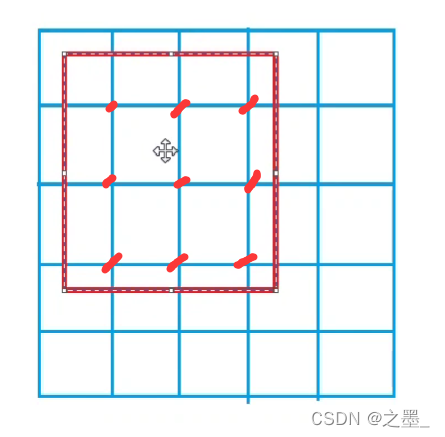

The weight of each point is abstracted into a two-dimensional array,Then find the prefix sum of the two-dimensional array,According to the input side length of the question, enumerate the weights of each rectangle satisfying the side length and select the maximum value

Such as when the side length is 3时,There can be one from1,1 到 3,3的 二维矩阵 计算权值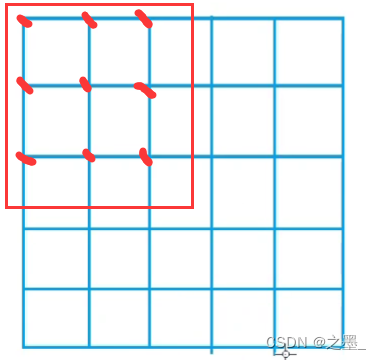

#include <stdio.h>
#include <algorithm>
using namespace std;   

const int N = 5010;
int s[N][N];
int n,r;
int mx,my;
int sum;

int main(){
    
    scanf("%d%d",&n,&r);
    r = min(5001,r);// 5001to cover the entire strike range
    mx = my = r;
    while(n--){
    
        int x,y,w;
        scanf("%d%d%d",&x,&y,&w);
        x++;y++;//To avoid boundary problems Start with coordinates1,1记录
        mx = max(x,mx);my = max(y,my);//Record the coordinate boundaries
        s[x][y] += w;//Record the target weights
    }
    //记录前缀和
    for(int i = 1;i <= mx;i++)
        for(int j = 1;j <= my;j++)
            s[i][j] += s[i-1][j]+s[i][j-1]-s[i-1][j-1];


    //Coordinates from the bottom right corner 枚举 边长为 r 的范围 计算 权重
    for(int i = r;i <= mx;i++)
        for(int j = r;j <= my ;j++)
            sum = max(sum,s[i][j] - s[i-r][j] - s[i][j-r] + s[i-r][j-r]);

    printf("%d\n",sum);
    
    return 0;
}

K倍区间(中等)

首先想到前缀和 然后暴力枚举 区间
代码很简单 但是 Unsurprisingly timed out The time complexity here seems to be yesO(n²)?

#include <stdio.h>

const int N = 1e5+10;
int a[N];
int n,k;
int sum;
int main(){
    
    scanf("%d%d",&n,&k);
    for(int i = 1;i <= n;i++){
    
        scanf("%d",&a[i]);
        a[i] += a[i-1];
    }
    for(int i = 1;i<=n;i++)
        for(int j = i;j<=n;j++)
             if((a[j] - a[j-i])%k == 0)
                sum++;
    printf("%d",sum);
}

The next step is to optimize the code
Known by the prefix sum 某个区间l - r的值等于 sum[r]- sum[l-1]
则（ sum[r] - sum[l-1]）%k = 0
可得 sum[r]%k == sum[l-1]%k
Then in two cases 存在k 倍区间

1. sum[r]%k == 0
2. A two-segment prefix and modulok余数相同

The specific approach is to open a count arraycnt[],cnt[i]is to calculate the remainder as iThe prefix sum of

需要注意的是初始化 cnt[0] = 1 否则得不到正确结果

因为：

Here is the use of prefix sum array to calculate the sum of a certain interval,前缀和数组s[0] = 0, s[i] = a[1] + a[2] + ... + a[i],If you want to counta[L] + a[L + 1] + ... + a[R],它的值就等于s[R] - S[L - 1],所以当L = 1的时候,就会用到s[0]了

cnt[0]存的是s[]中等于0的数的个数,由于s[0] = 0,所以最初等于0的有1个数,所以cnt[0] = 1

#include <stdio.h>

const int N = 1e5+10;
typedef long long ll;
ll a[N],cnt[N];
int n,k;
ll sum;
int main(){
    
    scanf("%d%d",&n,&k);
    for(int i = 1;i <= n;i++){
    
        scanf("%d",&a[i]);
        a[i] += a[i-1];
    }
    cnt[0]++;//cnt[] 保存的是a[]%k中值为0的个数 初始时 a[0] = 0（Prefix and subscript of the array0没有用到） So initially there is one
    for(int i = 1;i<=n;i++)
        {
    
            sum += cnt[a[i]%k];  //Counts the same amount as the remainder of the current value
            cnt[a[i]%k]++;       // current value modulok的数量+1
        }
    printf("%lld",sum);
}

买不到的数目(简单)

数论
裴蜀定理：对任何整数a,b和它们的最大公约数d,关于未知数x和y的线性不定方程（称为裴蜀等式）：若a,b是整数,且（a,b)=d,那么对于任意的整数x,y,ax+by都一定是d的倍数,特别地,一定存在整数x,y,使ax+by=d成立
它的一个重要推论是：a,b互质的充要条件是存在整数x,y使ax+by=1.

A mathematical formula can be derived,两个互质的数 The largest number that cannot be combined is (q-1)*p-q)

#include<iostream>
using namespace std;

int p,q;

int main()
{
    
    scanf("%d%d",&p,&q);
    printf("%d\n",(q-1)*p-q);
    return 0;
}

摘花生(简单)

#include <bits/stdc++.h>

using namespace std;

const int N = 110;
int peanut[N][N],peanuts[N][N];
int t;
int main(){
    
    cin>>t;
    while(t--){
    
        int r,c;
        cin >> r >> c;
        for(int i = 1 ;i <= r; i++)
            for(int j = 1 ;j <= c ; j++)
                cin >> peanut[i][j];
        
        for(int i = 1;i <= r ; i++)
            for(int j = 1;j <= c ;j++)
                peanuts[i][j] = max(peanuts[i-1][j],peanuts[i][j-1])+peanut[i][j];
                
        cout << peanuts [r][c] <<endl;
    }
    return 0;
}