当前位置:网站首页>AcWing 344. 观光之旅题解(floyd求无向图的最小环问题)
AcWing 344. 观光之旅题解(floyd求无向图的最小环问题)
2022-07-06 18:00:00 【乔大先生】
AcWing 344. 观光之旅
这题是利用floyd的性质求无向图的最小环问题,注意记录路径和求最小中间点的先后顺序和顺序的意义(因为要求的是环,先求环的时候,此时k还未更新成i、j之间最短的点,所以在path[cnt ++ ] = k和下一行的get_min中path[cnt ++ ] = k的k值不同,保证了是一个环)
#include<bits/stdc++.h>
using namespace std;
const int N = 110, INF = 0x3f3f3f3f;
int n, m;
int d[N][N], w[N][N]; //d储存最短路径,w储存边权值
int path[N];
int pos[N][N];
int cnt;
void get_path(int i, int j){
if(pos[i][j] == 0) return ;
int k = pos[i][j];
get_path(i, k); //找到i和中间点k之间经过的点并存入path数组中
path[cnt ++ ] = k;
get_path(k, j); //找到k和j之间经过的点并存入path数组中
}
signed main()
{
cin>>n>>m;
memset(w, 0x3f, sizeof w);
for(int i = 1; i <= n; i ++ ) w[i][i] = 0;
while(m -- ){
int a, b, c;
cin>>a>>b>>c;
w[a][b] = w[b][a] = min(w[a][b], c);
}
int res = INF;
memcpy(d, w, sizeof d);
for(int k = 1; k <= n; k ++ ){
//这里比较疑惑的是为什么先求路径,再找两点之间最短距离
//原因是,此时k还未更新成i、j之间最短的点
//所以在path[cnt ++ ] = k和下一行的get_min中path[cnt ++ ] = k的k值不同,保证了是一个环
//先求路径
for(int i = 1; i < k; i ++ ){
for(int j = i + 1; j < k; j ++ ){
if(res > (long long)d[i][j] + w[k][i] + w[j][k]){
//找到更小环
res = d[i][j] + w[k][i] + w[j][k]; //注意按照环的方向
cnt = 0; //重新记录路径
path[cnt ++ ] = k; //这个环是从k出发
path[cnt ++ ] = i;
get_path(i, j);
path[cnt ++ ] = j;
}
}
}
//求中间点
for(int i = 1; i <= n; i ++ ){
for(int j = 1; j <= n; j ++ ){
if(d[i][j] > d[i][k] + d[k][j]){
d[i][j] = d[i][k] + d[k][j];
pos[i][j] = k;
}
}
}
}
if(res == INF) cout<<"No solution."<<endl;
else{
for(int i = 0; i < cnt; i ++ ) cout<<path[i]<<' ';
cout<<endl;
}
return 0;
}
边栏推荐
- Amway wave C2 tools
- LeetCode:1175. Prime permutation
- Metauniverse urban legend 02: metaphor of the number one player
- taro3.*中使用 dva 入门级别的哦
- 编译命令行终端 swift
- 今日问题-2022/7/4 lambda体中修改String引用类型变量
- 【信号与系统】
- JTAG debugging experience of arm bare board debugging
- mysqlbackup 还原特定的表
- [100 cases of JVM tuning practice] 05 - Method area tuning practice (Part 2)
猜你喜欢
免费白嫖的图床对比
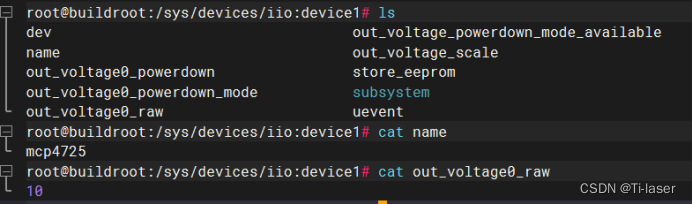
移植DAC芯片MCP4725驱动到NUC980

Clickhouse fields are grouped and aggregated, and SQL is queried according to the granularity of any time period

云呐-工单管理制度及流程,工单管理规范
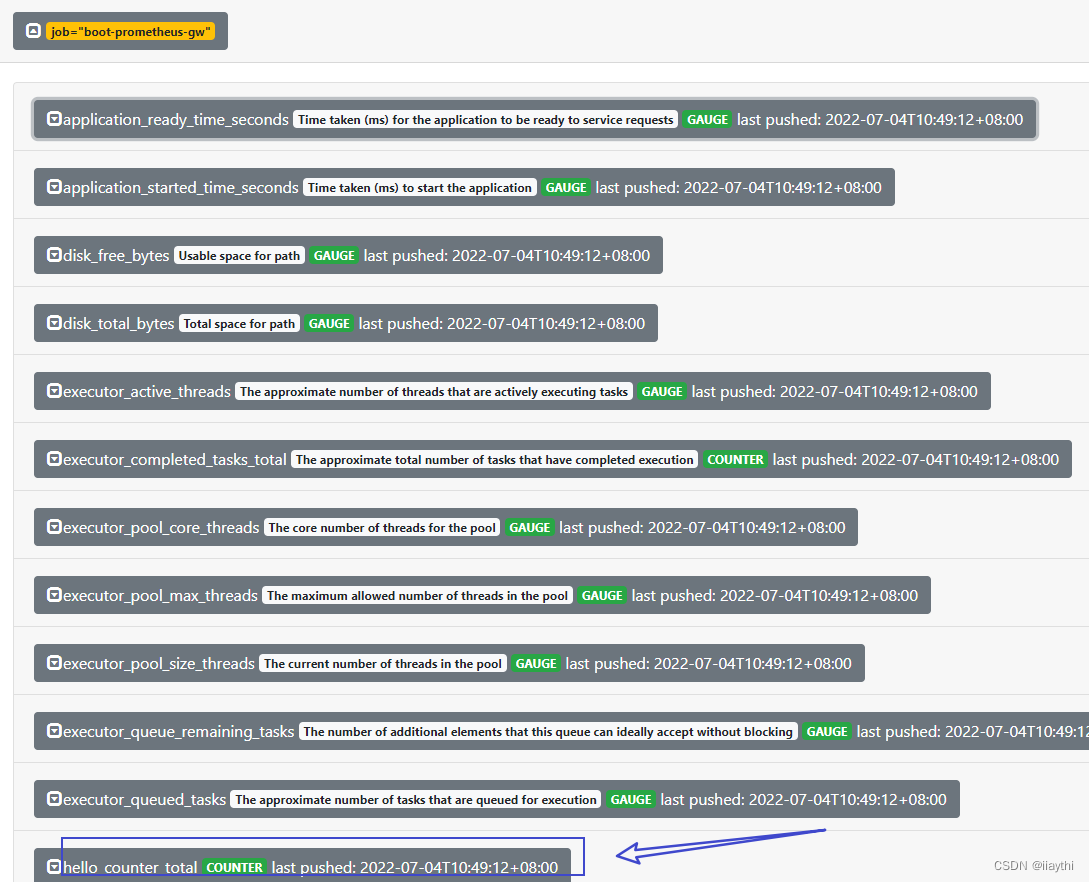
Boot - Prometheus push gateway use
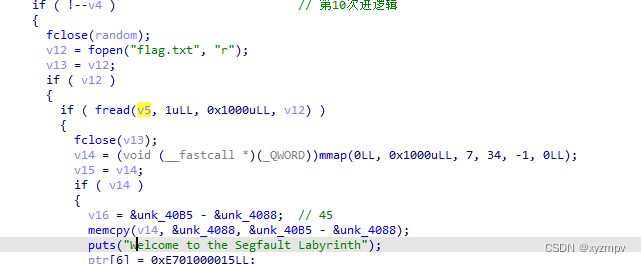
2022 Google CTF segfault Labyrinth WP
Your cache folder contains root-owned files, due to a bug in npm ERR! previous versions of npm which
Make Jar, Not War

对C语言数组的再认识
![JS reverse -- ob confusion and accelerated music that poked the [hornet's nest]](/img/40/da56fe6468da64dd37d6b5b0082206.png)
JS reverse -- ob confusion and accelerated music that poked the [hornet's nest]
随机推荐
图片打水印 缩放 和一个输入流的转换
Install Firefox browser on raspberry pie /arm device
今日问题-2022/7/4 lambda体中修改String引用类型变量
Meet in the middle
安全保护能力是什么意思?等保不同级别保护能力分别是怎样?
JS reverse -- ob confusion and accelerated music that poked the [hornet's nest]
JTAG debugging experience of arm bare board debugging
taro3.*中使用 dva 入门级别的哦
2022 Google CTF SEGFAULT LABYRINTH wp
字节P7专业级讲解:接口测试常用工具及测试方法,福利文
How to evaluate load balancing performance parameters?
Neon Optimization: an instruction optimization case of matrix transpose
分享一个通用的so动态库的编译方法
对C语言数组的再认识
C language instance_ three
[chip scheme design] pulse oximeter
tansig和logsig的差异,为什么BP喜欢用tansig
Installation and testing of pyflink
Clickhouse fields are grouped and aggregated, and SQL is queried according to the granularity of any time period
前置机是什么意思?主要作用是什么?与堡垒机有什么区别?