Optimal transport Series 1

Whereas Optimal Transport stay Machine Learning Widespread use in the field , I want to study it carefully Optimal Transport, There's a lot of information online , But because the author is stupid , It took me a long time to find the easy to understand materials . This blog aims to describe clearly in the simplest way Optimal transport, Due to limited mathematical ability , If there is any mistake, I hope you can correct it in time .

Prior Knowledge

L1 Distance: $d_{L_1}({\rho }_1,{\rho }_2)={\int }_{-\infty }^{+\infty }|{\rho }_1(x)-{\rho }_2(x)|dx$
KL divergence:$d_{KL}({\rho }_1||{\rho }_2)={\int }_{-\infty }^{+\infty }{\rho }_1(x)log\frac{{\rho }_1(x)}{{\rho }_2(x)}dx$
If you want to measure the above figure ( From references 1) in ${\rho }_1$ To ${\rho }_2$ The distance and ${\rho }_1$ To ${\rho }_3$ Distance of , Can be found using L1 Distance and KL divergence All fail , All the results are the same .

Be careful ： by the way L1 Distance Come on , The same distance is easy to understand , Because it calculates the area of two distributions . And for KL divergence Come on , First of all, it should be noted that it is not a distance measure ,Because it is not symmetric: the KL from ${\rho }_1(x)$ to ${\rho }_2(x)$ is generally not the same as the KL from ${\rho }_1(x)$ to ${\rho }_2(x)$. Furthermore, it need not satisfy triangular inequality. We will Kullback-Leibler Divergence Change the form to get $$d_{KL}({\rho }_1||{\rho }_2)={\int }_{-\infty }^{+\infty }{\rho }_1(x)log({\rho }_1(x))-{\rho }_1(x)log({\rho }_2(x))dx$$ And then put ${\rho }_1(x)log({\rho }_1(x))$ and ${\rho }_1(x)log({\rho }_2(x))$ Consider two new distributions , Then it is also transformed into the area relationship , Because the former one is the same , Therefore, it mainly depends on the difference of the latter item . For better understanding , Author use python Write a simple demo： Be careful , Here I found a big problem ！！！

import math
import numpy as np
import matplotlib.pyplot as plt


def guassian(u, sig):
    #  mean value μ,  Standard deviation δ
    x = np.linspace(-30, 30, 1000000)   #  Domain of definition 
    y = np.exp(-(x - u) ** 2 / (2 * sig ** 2)) / (math.sqrt(2*math.pi)*sig) #  Define curve function 
    return x, y

x1, y1 = guassian(u=0, sig=math.sqrt(1))
x2, y2 = guassian(u=1, sig=math.sqrt(1))
x3, y3 = guassian(u=2, sig=math.sqrt(1))
plt.plot(x1,y1)
plt.plot(x2,y2)
plt.plot(x3,y3)

z1 = y1 * np.log2(y1) - y1 * np.log2(y2)
z2 = y1 * np.log2(y1) - y1 * np.log2(y3)
# plt.plot(x1, z1)
# plt.plot(x1, z2)
print(np.sum(z1))
print(np.sum(z2))

It is found through experiments that , The results of the experiment were quite different from what was expected , I use KL divergence Calculation ${\rho }_1$ To ${\rho }_2$ The distance and ${\rho }_1$ To ${\rho }_3$ The distance is not the same , Difference is very big ！！！

I visualized the distribution curve of the latter term , Found it completely different , And the value after integration is completely different .（ Here I take into account the effect that continuity becomes discreteness , So it was adjusted x Coordinate range and number of points drawn , Do not have what difference ） Later, it was found that , It seems that the curve given in the article is not a Gaussian curve , I feel a little misled , So I changed an example to calculate , Although it is a discrete distribution , But it can still directly reflect the problem （PS, In fact, I'm curious about why Gaussian distribution can't be used , Does anyone know why ）：

It can be found that for the above distribution ,L1 Distance and KL divergence All failed .

Optimal Transport

Last section L1 Distance and KL divergence The problem is , This section describes in detail Optimal Transport, First define the problem .Optimal Transport The core of is how to find an optimal transformation to transform one distribution into another , And to minimize the conversion loss .（ Be careful ： The distribution here can be continuous or discrete ） Here we use the ${\rho }_1$ and ${\rho }_2$ give an example ：
For ease of understanding , We can ${\rho }_1$ and ${\rho }_2$ Imagine a pile of sand , that Optimal Transport The question becomes how to make ${\rho }_1$ The shape of the sand piled up ${\rho }_2$ The appearance of , And do the least work .$\pi (x,y)$ For from x How much quality of sand is moved to the location y Location , So clearly ${\rho }_1(x)$ Express x How much quality of sand is there in the location （ In plain English x Height of the position curve ）. So the problem can be expressed by the following formula ：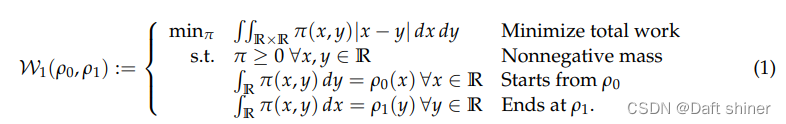

The objective function is to minimize the work done by handling , Because the mass of sand transported should be greater than or equal to 0, So the first constraint is easy to understand , As for articles 2 and 3 , Is to satisfy its initial and final distribution .This amount of work is known as the 1-Wasserstein distance in optimal transport. Next, we generalize it to p-Wasserstein distance:

It is also easy to understand , Only the distance of transportation has changed . After the problem is defined , So how can we get this $\pi (x,y)$ Well ？

Discrete Problems in One Dimension

For one-dimensional problems, there are the above two cases ：D2D,D2C. about D2D The data of , We first relax the original distribution function $\rho (x)$ To ${\mu }_0,{\mu }_1\in Prob(\mathbb{R})$,Define the Dirac $\delta$-measure centered at $x\in \mathbb{R}$ via (:= In mathematics it is defined as )
$${\delta }_x(S):=\{\begin{array}{ll}1,& ifx\in S\\ 0,& Otherwise.\end{array}$$ here ${\mu }_0,{\mu }_1$ Respectively ：

among ${\sum }_i{a}_{0i}={\sum }_i{a}_{1i}=1$,$a_{0i},a_{1i}\ge 0$. I think it's $S$ yes $[x_{01},x_{02},\cdots ,x_{0k_0}]$ Subset . At this time, the calculation of the problem is ：

The same way as the above explanation ,$T_{ij}$ From $x_{0i}$ Transport to $x_{1j}$ The quality of the .$|x_{0i}-x_{1j}{|}^p$ It's from $x_{0i}$ Transport to $x_{1j}$ Distance of .$T_{ij}$ The transportation mass shall be greater than or equal to 0,$x_{0i}$ and $x_{1j}$ The mass at the point must satisfy the conservation condition . requirement $T_{ij}$, This is a finite element linear programming , Many classical algorithms can be used to solve , for example simplex or interior point methods. And for D2C The situation of , Each discrete ${\mu }_0$ Are mapped to a continuous interval ${\mu }_1$, As shown in the figure below ：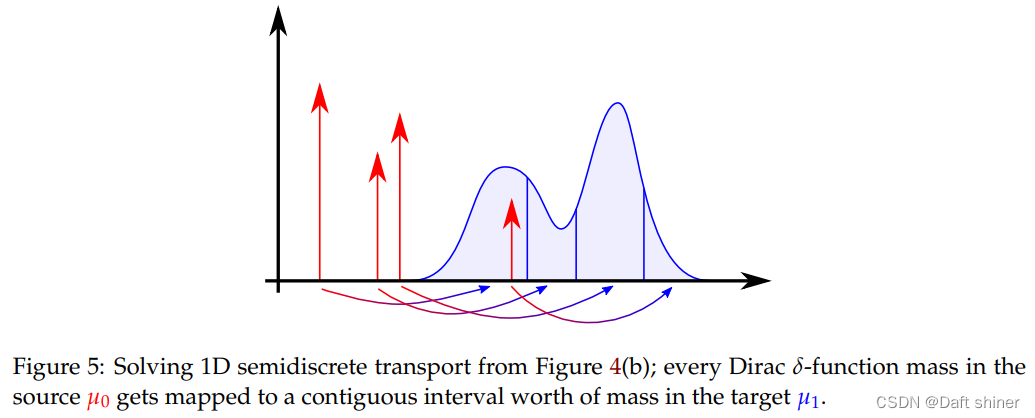

Conclusion

This section focuses on Optimal Transport Two forms of （D2C,D2D), The next section will cover more general In the form of .

References

[1] Optimal Transport on Discrete Domains
[2] Kullback-Leibler Divergence
[3] Optimal Transport and Wasserstein Distance