组合系列--有排列就有组合

组合的题目的重点就是顺序问题，他不像排列，不同顺序代表一个排列，所以组合的遍历。当然最后一题是题目自己定义组合的，所以会有所不同。

77. 组合

选择1~n中的k个数，构造出所有组合，其中每个数不可重复使用（隐含条件）

力扣传送门

思路：DFS，回溯

1. 参数说明：
   pre，用于记录上一个数的下标，注意组合跟排列不一样，组合跟顺序没关系，也就是12和21是一样的，所以需要避免重复组合。==具体做法就是保证组合中元素的下标是有序的就行，也就是当前遍历到的元素的下标要大于上一个，也就是pre<i。需要注意的是，这里的pre初始化是0，而不是-1，因为给定元素是1-n，直接用1-n的下标对应即可。
   layer，代表递归层数，或者说第几个组合数，k代表一个组合有k个数，当layer==k +1时，说明已经找到k个数，直接保存组合结果，无需再进行递归了。
2. 剪枝条件： k-layer > n-i
k-layer代表组合还差几个数，n-i代表还剩几个数可选择。如果组合需要的个数超过可选择的，说明可选择数不够，无法凑成组合，直接return。例如12345，k=4，layer=1，i=4，假如选择的第一个组合数是3，还差3个，但可用的只有4和5两个数，所以直接返回

不加剪枝，代码也对，剪枝是为了提高效率，减少不必要的计算。

class Solution {
    
	//仅仅只是记录组合结果，你也可以用list集合代替
    private boolean[] record;
    //结果 
    private List<List<Integer>> res;
    
    public List<List<Integer>> combine(int n, int k) {
    
        record = new boolean[n + 1];
        res = new ArrayList<>();
        dfs(n, k, 0, 1);
        return res;
    }
    
    public void dfs(int n, int k, int pre, int layer) {
    
        //边界
        if (layer == k + 1) {
    
            //也可用List集合
            Integer[] zuhe = new Integer[k];
            int idx=0;
            for (int i = 1; i <=n; i++) {
    
                 if (record[i]) {
    
                     zuhe[idx++] = i;
                 }
            }
            res.add(Arrays.asList(zuhe));
            return;
        }
        //递归
        for (int i = 1; i <= n; i++) {
    
            //剪枝
            if(k - layer > n - i) {
     
                return;
            }                        
            if (pre < i) {
    
                record[i] = true;
                dfs(n, k, i, layer + 1);
                record[i] = false;
            }
        }    
    }
}

️优化：对于pre<i，由于pre记录的是上一个数的下标，那么下层递归循环时，直接让i=pre+1，去掉对1~pre这部分的if判断，不然每次for循环都是1-n的判断。后面的题目也会采用下面这种方式

     //递归，修改i=pre+1
     for (int i = pre + 1; i <= n; i++) {
    
         //剪枝
         if(k - layer > n - i) {
    
             return;
         }                        
         record[i] = true;
         dfs(n, k, i, layer + 1);
         record[i] = false;
     }    

39. 组合总和

给定无重复元素的数组，求元素和为target的所有组合，且每个元素能在一个组合中使用多次

力扣传送门

思路：DFS，回溯

1. 虽然题目说同一元素可重复使用，但顺序还是不可变，也就是12和21是一样的组合。跟上一题一样，顺序问题同样用pre来记录上一个元素，由于可重复，需要讲i=pre+1 改为 i=pre
2. 由于每个组合大小不确定，不适合用记录数组record进行标记，可用集合代替，选择就添加到集合末尾，不选择就从末尾移除。
3. 剪枝也有所变化，这跟求解目标有关，也就是组合的和要等于target，那就意味大于的直接跳过。（不是return，因为这里candidates数组的元素不一定有序，你无法保证后面的元素一定更大，除非，你先用快排）

class Solution {
    
	//记录每个组合 
    private List<Integer> zuhe; 
    //结果
    private List<List<Integer>> res; 

    public List<List<Integer>> combinationSum(int[] candidates, int target) {
    
        res = new ArrayList<>();
        zuhe = new ArrayList<>();
        dfs(candidates, target, 0, 0);
        return res;
    }

    private void dfs(int[] candidates, int target, int sum, int pre) {
       

        if (sum == target) {
    
            res.add(new ArrayList<>(zuhe));
            return;
        } 
               
        int l = candidates.length;
        //由于可重复选，i=pre
        for (int i = pre; i < l; i++) {
    
            //剪枝
            if(sum + candidates[i] > target) {
    
                continue;
            }
            zuhe.add(candidates[i]); //选择添加
            dfs(candidates, target, sum + candidates[i], i);
            zuhe.remove(zuhe.size() - 1); //不选移除
        }
    }
}

前两道题都是针对无重复元素

40. 组合总和 II

给定存在重复元素的数组，求元素和为target的组合，且每个元素不可重复使用

力扣传送门

思路：DFS，回溯

1. 由于每个元素不可重复使用，跟第一道题类似，通过pre保存上一个元素的下标，这样下一层遍历i=pre+1就能避免再次访问上一个元素。
2. 但该题还有一个最大的问题，数组存在重复元素，例如，1121，target=3，会出现1211和1211的情况（pre仅仅只是保证访问顺序问题），问题就在于重复数字的访问没有按序访问，也就是对于21，1的前面存在重复数字，但还未访问，此时如果访问就会出现重复，所以我们只需要保证访问重复数字时，其前面的重复数字一定要访问过。具体做法就是跟前一个数做比较（前提是需要对数组排序）例如1211排序后就是1112，假如组合数的第一个数选i=1，此时[i]==[i-1]，也就是存在为0的重复的数还没访问过，我没资格访问，继续下一个，i=2,此时[i]==[i-1], 没资格访问，只有i=0时被访问过，i=1才能访问，i=1访问过，i=2才能访问。本质就是保证就是在递归树中，同一层的点不能有重复的元素。大体如下图，红色代表不可访问。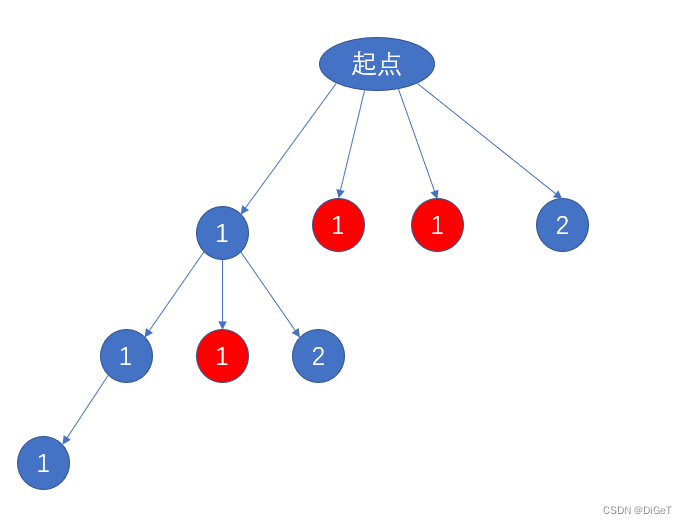
   
3. 由于每个组合大小不确定，同理用集合进行保存组合结果，选择就添加到集合末尾，不选择就从末尾移除。
4. 剪枝，同上，且这里可直接return，因为数组有序，往后遍历，结果只会更大

class Solution {
     
    private List<Integer> zuhe; 
    private List<List<Integer>> res;

    public List<List<Integer>> combinationSum2(int[] candidates, int target) {
    
        res = new ArrayList<>();
        zuhe = new ArrayList<>();        
        //排序
        Arrays.sort(candidates);     
        //pre为-1是因为数组下标从0开始，注意和第一题的区别
        dfs(candidates, target, 0, -1); 
        return res;
    }

    private void dfs(int[] candidates, int target, int sum, int pre) {
       

        if (sum == target) {
    
            res.add(new ArrayList<>(zuhe));
            return;
        }        
        int l = candidates.length;

        for (int i = pre+1; i < l; i++) {
    
        	//pre+1不需要判断，因为前一个元素一定访问过了(上一层)
            if(i>pre+1 && candidates[i]==candidates[i-1]) continue;
            //剪枝
            if(sum + candidates[i] > target) {
    
                return; //直接返回
            }
            zuhe.add(candidates[i]); //添加
            dfs(candidates, target, sum + candidates[i], i);
            zuhe.remove(zuhe.size() - 1); //移除
        }
    }
}

216. 组合总和 III

给定1-9的数组，挑出k个数构成和为n的组合，且每个元素只能在组合中用一次。

相比前面两道，这道反而是比较简单的。

力扣传送门

思路：DFS，回溯

1. 跟第一道求组合一样，数组是固定的，只不过多了求组合的和，顺序问题同样用pre来记录上一个元素
2. 组合大小确定，可以用记录数组record进行标记，也可用集合
3. 剪枝有两个，当组合的和要等于target，那就意味大于的直接返回。还有就是元素个数，也就是k > 10-i直接返回，这里用k递减，所以没有第一题的layer

class Solution {
    

    private List<Integer> record; 
    private List<List<Integer>> res; 

    public List<List<Integer>> combinationSum3(int k, int n) {
            
        record = new ArrayList<>();
        res = new ArrayList<>();
        dfs(k, n, 0, 0);
        return res;
    }

    public void dfs(int k, int n, int sum, int pre) {
    
		//边界
        if (k == 0 && sum == n) {
    
            res.add(new ArrayList<>(record));
            return;
        }

        for (int i = pre + 1; i <= 9; i++) {
    
            //剪枝
            if (sum + i > n || k > 10-i) {
    
                return;
            }
            record.add(i); //添加
            dfs(k - 1, n, sum + i, i);
            record.remove(record.size() - 1); //移除
        }
    }
}

377. 组合总和 Ⅳ

给定无重复元素的数组，求元素和为target的所有组合的个数，且每个元素能在一个组合中使用多次，且112和211不一样，由于没顺序，所以不需要pre，但是需要剪枝，因为数据过大，容易超时。

https://leetcode.cn/problems/combination-sum-iv/

思路：dfs + 缓存（也就是网上常说的记忆化搜索），其实就是保存一些递归好的结果，从而通过剪枝避免重复计算
例如：如果不缓存，下面例子超时
[10,20,30,40,50,60,70,80,90,100,110,120,130,140,150,160,170,180,190,200,210,220,230,240,250,260,270,280,290,300,310,320,330,340,350,360,370,380,390,400,410,420,430,440,450,460,470,480,490,500,510,520,530,540,550,560,570,580,590,600,610,620,630,640,650,660,670,680,690,700,710,720,730,740,750,760,770,780,790,800,810,820,830,840,850,860,870,880,890,900,910,920,930,940,950,960,970,980,990,111]
999

class Solution {
    
    //记录剩余值缓存
    int[] cache;

    public int combinationSum4(int[] nums, int target) {
    
        cache = new int[target+1];      
        //注意初始化不能是0，因为0也可以缓存，你如果用hashmap就知道为什么了，因为hashmap也会对0进行缓存
        Arrays.fill(cache, -1);
        int count = dfs(nums,target);
        return count;
    }

    public int dfs(int[] nums, int rest) {
           
        if(rest == 0) {
    
            return 1;
        }          
        //错误判断if(cache[rest] != 0)
        //根据缓存剪枝，正确的判断
        if(cache[rest] != -1) return cache[rest];      

        int l = nums.length;
        int sum = 0;
        for(int i = 0; i < l; i++) {
    
            if(nums[i] <= rest) {
    
                sum += dfs(nums, rest - nums[i]);
            }
        }
        cache[rest] = sum; //缓存 
        return sum;
    }
}