当前位置:网站首页>一元二次方程到规范场
一元二次方程到规范场
2022-06-23 16:51:00 【小的时候可菜了】
曹则贤开讲“从一元二次方程到规范场论” 中国科学院2022跨年科学演讲第三场全程回顾
一元二次方程式两根推导
a x 2 + b x + c = a ( x 2 + b a x ) + c = a ( x 2 + b a x + b 2 4 a 2 − b 2 4 a 2 ) + c = a ( x + b 2 a ) 2 − b 2 4 a + 4 a c 4 a \begin{aligned} &ax^2+bx+c \\ &=a(x^2+\frac{b}{a}x)+c \\ &=a(x^2+\frac{b}{a}x+\frac{b^2}{4a^2}-\frac{b^2}{4a^2})+c \\ &=a(x+\frac{b}{2a})^2-\frac{b^2}{4a}+\frac{4ac}{4a} \end{aligned} ax2+bx+c=a(x2+abx)+c=a(x2+abx+4a2b2−4a2b2)+c=a(x+2ab)2−4ab2+4a4ac
移项,得
a ( x + b 2 a ) 2 = b 2 − 4 a c 4 a ( x + b 2 a ) 2 = b 2 − 4 a c 4 a 2 x + b 2 a = ± b 2 − 4 a c 2 a x = − b ± b 2 − 4 a c 2 a a(x+\frac{b}{2a})^2=\frac{b^2-4ac}{4a} \\ (x+\frac{b}{2a})^2=\frac{b^2-4ac}{4a^2} \\ x+\frac{b}{2a}=\frac{\pm\sqrt{b^2-4ac}}{2a} \\ x=\frac{-b\pm\sqrt{b^2-4ac}}{2a} a(x+2ab)2=4ab2−4ac(x+2ab)2=4a2b2−4acx+2ab=2a±b2−4acx=2a−b±b2−4ac
二次函数交点式推导
假设其两根为 x 1 x_1 x1、 x 2 x_2 x2,则有
x 1 = − b + b 2 − 4 a c 2 a x 2 = − b − b 2 − 4 a c 2 a x_1=\frac{-b+\sqrt{b^2-4ac}}{2a} \\ x_2=\frac{-b-\sqrt{b^2-4ac}}{2a} x1=2a−b+b2−4acx2=2a−b−b2−4ac
x 1 + x 2 x_1+x_2 x1+x2与 x 1 x 2 x_1x_2 x1x2的结果为
x 1 + x 2 = − b + b 2 − 4 a c 2 a + − b − b 2 − 4 a c 2 a = − b a x 1 x 2 = ( − b ) 2 − ( b 2 − 4 a c ) 2 4 a 2 = c a x_1 + x_2=\frac{-b+\sqrt{b^2-4ac}}{2a}+\frac{-b-\sqrt{b^2-4ac}}{2a}=-\frac{b}{a} \\ x_1x_2=\frac{(-b)^2-(\sqrt{b^2-4ac})^2}{4a^2}=\frac{c}{a} x1+x2=2a−b+b2−4ac+2a−b−b2−4ac=−abx1x2=4a2(−b)2−(b2−4ac)2=ac
a x 2 + b x + c 处 理 为 下 列 式 子 , 方 便 之 后 好 用 x 1 , x 2 替 代 = a ( x 2 + b a x + c a ) 将 式 中 的 b a 、 c a 用 x 1 、 x 2 表 示 = a ( x 2 − ( x 1 + x 2 ) x + x 1 x 2 ) = a [ ( x − x 1 ) ( x − x 2 ) ] \begin{aligned} &ax^2+bx+c \\ &处理为下列式子,方便之后好用x_1,x_2替代 \\ &=a(x^2+\frac{b}{a}x+\frac{c}{a}) \\ &将式中的 \frac{b}{a}、\frac{c}{a}用~x_1、x_2表示 \\ &=a(x^2-(x_1+x_2)x+x_1x_2) \\ &=a[(x-x_1)(x-x_2)] \\ \end{aligned} ax2+bx+c处理为下列式子,方便之后好用x1,x2替代=a(x2+abx+ac)将式中的ab、ac用 x1、x2表示=a(x2−(x1+x2)x+x1x2)=a[(x−x1)(x−x2)]
用根自身来表示根
x 1 , 2 = − b ± b 2 − 4 a c 2 a 处 理 为 下 列 式 子 , 方 便 之 后 好 用 x 1 , x 2 替 代 = − 1 2 b a ± 1 4 ( b a ) 2 − c a 将 式 中 的 b a 、 c a 用 x 1 、 x 2 表 示 = 1 2 ( x 1 + x 2 ) ± 1 4 ( x 1 + x 2 ) 2 − x 1 x 2 \begin{aligned} &x_{1,2}=\frac{-b\pm\sqrt{b^2-4ac}}{2a} \\ &处理为下列式子,方便之后好用x_1,x_2替代 \\ &=-\frac{1}{2}\frac{b}{a}\pm\sqrt{\frac{1}{4}(\frac{b}{a})^2-\frac{c}{a}} \\ &将式中的 \frac{b}{a}、\frac{c}{a}用~x_1、x_2表示 \\ &=\frac{1}{2}(x_1+x_2)\pm\sqrt{\frac{1}{4}(x_1+x_2)^2-x_1x_2} \\ \end{aligned} x1,2=2a−b±b2−4ac处理为下列式子,方便之后好用x1,x2替代=−21ab±41(ab)2−ac将式中的ab、ac用 x1、x2表示=21(x1+x2)±41(x1+x2)2−x1x2
一元三次方程
( a + b ) 3 = a 3 + b 3 + 3 a b ( a + b ) ( a − b ) 3 = a 3 − b 3 − 3 a b ( a − b ) (a+b)^3=a^3+b^3+3ab(a+b) \\ (a-b)^3=a^3-b^3-3ab(a-b) (a+b)3=a3+b3+3ab(a+b)(a−b)3=a3−b3−3ab(a−b)
求解一元三次方程 x 3 + p x + q x^3+px+q x3+px+q,方法:约化,把一元三次方程约化成一元二次方程
令 x = u 1 3 + v 1 3 x 3 + p x + q = u + v + 3 u 1 3 v 1 3 ( u 1 3 + v 1 3 ) + p ( u 1 3 + v 1 3 ) + q = ( u + v + q ) + ( 3 u 1 3 v 1 3 + p ) ( u 1 3 + v 1 3 ) = ( u + v + q ) + ( 3 u 1 3 v 1 3 + p ) ( x ) 因 此 有 u + v + q = 0 3 u 1 3 v 1 3 + p = 0 → u 1 3 v 1 3 = − p 3 → u v = − ( p 3 ) 3 → v = − ( p 3 ) 3 1 u 代 入 上 式 u + − ( p 3 ) 3 1 u + q = 0 → u 2 + q u − ( p 3 ) 3 = 0 ( 一 元 三 次 方 程 → 一 元 二 次 方 程 ) u = − q ± q 2 + 4 ( p 3 ) 3 2 = − q 2 ± q 2 4 + ( p 3 ) 3 v = − q − u = − q ∓ q 2 + 4 ( p 3 ) 3 2 = − q 2 ∓ q 2 4 + ( p 3 ) 3 x = ( − q 2 ± q 2 4 + ( p 3 ) 3 ) 1 3 + ( − q 2 ∓ q 2 4 + ( p 3 ) 3 ) 1 3 \begin{aligned} &令x=u^{\frac{1}{3}}+v^{\frac{1}{3}} \\ &x^3+px+q \\ &=u+v+3u^{\frac{1}{3}}v^{\frac{1}{3}}(u^{\frac{1}{3}}+v^{\frac{1}{3}})+p(u^{\frac{1}{3}}+v^{\frac{1}{3}})+q \\ &=(u+v+q)+(3u^{\frac{1}{3}}v^{\frac{1}{3}}+p)(u^{\frac{1}{3}}+v^{\frac{1}{3}}) \\ &=(u+v+q)+(3u^{\frac{1}{3}}v^{\frac{1}{3}}+p)(x) \\ &因此有 \\ &u+v+q=0 \\ &3u^{\frac{1}{3}}v^{\frac{1}{3}}+p=0 \to u^{\frac{1}{3}}v^{\frac{1}{3}}=-\frac{p}{3} \to uv=-(\frac{p}{3})^3 \to v=-(\frac{p}{3})^3\frac{1}{u} 代入上式 \\ &u+-(\frac{p}{3})^3\frac{1}{u}+q=0 \to u^2+qu-(\frac{p}{3})^3=0(一元三次方程\to一元二次方程) \\ &u=\frac{-q\pm\sqrt{q^2+4(\frac{p}{3})^3}}{2}=-\frac{q}{2}\pm\sqrt{\frac{q^2}{4}+(\frac{p}{3})^3} \\ &v=-q-u=\frac{-q\mp\sqrt{q^2+4(\frac{p}{3})^3}}{2}=-\frac{q}{2}\mp\sqrt{\frac{q^2}{4}+(\frac{p}{3})^3} \\ &x=(-\frac{q}{2}\pm\sqrt{\frac{q^2}{4}+(\frac{p}{3})^3})^\frac{1}{3}+(-\frac{q}{2}\mp\sqrt{\frac{q^2}{4}+(\frac{p}{3})^3})^\frac{1}{3} \end{aligned} 令x=u31+v31x3+px+q=u+v+3u31v31(u31+v31)+p(u31+v31)+q=(u+v+q)+(3u31v31+p)(u31+v31)=(u+v+q)+(3u31v31+p)(x)因此有u+v+q=03u31v31+p=0→u31v31=−3p→uv=−(3p)3→v=−(3p)3u1代入上式u+−(3p)3u1+q=0→u2+qu−(3p)3=0(一元三次方程→一元二次方程)u=2−q±q2+4(3p)3=−2q±4q2+(3p)3v=−q−u=2−q∓q2+4(3p)3=−2q∓4q2+(3p)3x=(−2q±4q2+(3p)3)31+(−2q∓4q2+(3p)3)31
方程根之间的等价性
一个方程若有个多个根,但根未知,则这些根之间都是等价的
比如,一个方程里面有一个根,一个是4,一个是3,许多人很容易误解4大于3,但是就这个方程本身来说,如果3、4都是这个方程的根,是一样的,是等价
代数方程的一般形式: ( x − x 1 ) ( x − x 2 ) … ( x − x n ) = 0 (x-x_1)(x-x_2)…(x-x_n)=0 (x−x1)(x−x2)…(x−xn)=0,从该角度来理解到底有多少根的时候,这个方程是有解的
复数的几何意义
有一个长度为 a a a的线段,根据一点,将其分为两段,使得 x ( a − x ) = a 2 2 x(a-x)=\frac{a^2}{2} x(a−x)=2a2成立,求 x x x的值,也就是点在线段上的位置
x ( a − x ) = a 2 2 x 2 − a x + a 2 2 = 0 x 1 , 2 = a 2 + ( ± a 2 − 2 a 2 2 ) = a 2 + ( ± a i 2 ) \begin{aligned} &x(a-x)=\frac{a^2}{2} \\ &x^2-ax+\frac{a^2}{2}=0 \\ &x_{1,2}=\frac{a}{2}+(\pm\frac{\sqrt{a^2-2a^2}}{2})=\frac{a}{2}+(\pm\frac{ai}{2}) \end{aligned} x(a−x)=2a2x2−ax+2a2=0x1,2=2a+(±2a2−2a2)=2a+(±2ai)
x x x的解当中存在虚数,说明题中要求的将线段分成两截的点不在线段上
法国人比埃(Adrien-Quentin Buée, 1748-1826)认为,这个方程根意味着分割点 x x x是在线段的上方或者下方——那个 i i i 指向垂直方向
复数是一个从一维空间向二维空间扩展的概念
小女孩可能对方向的概念不是那么理解,她妈妈问她:“你现在是在我的左边还是右边?”,小女孩想了想,答道:“旁边”
四元数的引入
复数能够表示我们二维平面里面的转动
比如:在一个坐标轴上, 3 ± 1 = ( 2 , 4 ) 3\pm1=(2,4) 3±1=(2,4)在一条直线上,而 a ± i b a±ib a±ib 变成平面的扩展
但有人说,我们生活的空间不是二维而是三维的,所以,是否有一个数,使得能够在二维空间描述的物理同样适应于三维空间?
所以有人想,是否可以把 a ± i b a±ib a±ib这样一个描述二维的数给表示成描述三维的数?
从 2 D → 3 D 2D\to3D 2D→3D: z = a + b i → z = a + b i + c j z=a+bi \to z=a+bi+cj z=a+bi→z=a+bi+cj,其中 i 2 = − 1 , j 2 = − 1 i^2=-1, j^2=-1 i2=−1,j2=−1
两个相同三元数(三个未知数)的乘积如下
( a + b i + c j ) ( a + b i + c j ) = ( a 2 − b 2 − c 2 ) + ( 2 a b ) i + ( 2 a c ) j + b c ( i j + j i ) (a+bi+cj)(a+bi+cj)=(a^2-b^2-c^2)+(2ab)i+(2ac)j+bc(ij+ji) (a+bi+cj)(a+bi+cj)=(a2−b2−c2)+(2ab)i+(2ac)j+bc(ij+ji)
上式多出来了一项, 𝑏 𝑐 ( 𝑖 𝑗 + 𝑗 𝑖 ) 𝑏𝑐 (𝑖𝑗 + 𝑗𝑖) bc(ij+ji),如果令 i j = 0 或 i j = − j i ij=0或ij=-ji ij=0或ij=−ji ,可变为三项
数学中的项:基本算术单元,如: a x 2 + b x + c = 0 ( a ≠ 0 ) ax^2+bx+c=0(a\not=0) ax2+bx+c=0(a=0) 中, a x 2 ax^2 ax2叫作二次项, a a a是二次项系数; b x bx bx叫作一次项, b b b是一次项系数; c c c叫作常数项
但是,两个任意三元数的乘积,两个任意三元数模平方的乘积,结果都是四项
( a 2 + b 2 + c 2 ) ( x 2 + y 2 + z 2 ) = ( a x − b y − c z ) 2 + ( a y + b x ) 2 + ( a z + c x ) 2 + ( b z − c y ) 2 (a^2+b^2+c^2)(x^2+y^2+z^2)=(ax-by-cz)^2+(ay+bx)^2+(az+cx)^2+(bz-cy)^2 (a2+b2+c2)(x2+y2+z2)=(ax−by−cz)2+(ay+bx)2+(az+cx)2+(bz−cy)2
哈密顿和他的夫人在沿着爱尔兰运河去开会的路上突然灵光一现,说既然两个三元数乘积永远等于四项,那从一开始就是四项不就完了吗?
于是令: q = a + b i + c j + d k q=a+bi+cj+dk q=a+bi+cj+dk,其中 i j = k , i k = j , j k = i , i j = − j i , i k = − k i , j k = − k j , i 2 = j 2 = k 2 = i j k = − 1 ij=k,ik=j,jk=i,ij=-ji,ik=-ki,jk=-kj,i^2=j^2=k^2=ijk=-1 ij=k,ik=j,jk=i,ij=−ji,ik=−ki,jk=−kj,i2=j2=k2=ijk=−1
四元数的乘积之后,结果太长,需对其简化,于是提出了一个新的概念
q = a + b i + c j + d k = r + v q=a+bi+cj+dk=r+v q=a+bi+cj+dk=r+v, r r r 为标量, v = b i + c j + d k v=bi+cj+dk v=bi+cj+dk 为矢量
( r 1 , v 1 ) + ( r 2 , v 2 ) = ( r 1 + r 2 , v 1 + v 2 ) ( r 1 , v 1 ) ( r 2 , v 2 ) = ( r 1 r 2 − v 1 v 2 , r 1 v 2 + r 2 v 1 + v 1 v 2 ) 矢 量 点 乘 矢 量 叉 乘 ( 0 , v 1 ) ( 0 , v 2 ) = ( − v 1 v 2 , v 1 v 2 ) \begin{aligned} &(r_1,v_1)+(r_2,v_2)=(r_1+r_2,~~~v_1+v_2) \\ &(r_1,v_1)(r_2,v_2)=(r_1r_2-v_1v2,~~~r_1v_2+r_2v_1+v_1v_2) \\ &~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~矢量点乘~~~~~~~~~~~~~~~~~矢量叉乘 \\ &(0,v_1)(0,v_2)=(-v_1v2,~~~v_1v_2) \\ \end{aligned} (r1,v1)+(r2,v2)=(r1+r2, v1+v2)(r1,v1)(r2,v2)=(r1r2−v1v2, r1v2+r2v1+v1v2) 矢量点乘 矢量叉乘(0,v1)(0,v2)=(−v1v2, v1v2)
矢量可以有长度、有方向,但是,长度和方向不一定是必须的,也可以没有
边栏推荐
- [JS reverse hundred examples] pedata encryption information and zlib Application of gunzipsync()
- 全局组织结构控制之抢滩登陆
- 百度智能云5月产品升级观察站
- 论文阅读 (54):DeepFool: A Simple and Accurate Method to Fool Deep Neural Networks
- Hapoxy-集群服务搭建
- Skills that all applet developers should know: applying applet components
- Latex使用\usepackage{hyperref}报错:paragraph ended before [email protected]@link was complete
- January 5, 2022: there are four kinds of rhythms: AABB, ABAB and ABB
- Performance test bottleneck tuning in 10 minutes! If you want to enter a large factory, you must know
- [WebSocket] 开发在线客服系统知识点-websocket返回状态码的含义
猜你喜欢
![[mae]masked autoencoders mask self encoder](/img/08/5ab2b0d5b81c723919046699bb6f6d.png)
[mae]masked autoencoders mask self encoder

Crmeb second open SMS function tutorial

论文阅读 (53):Universal Adversarial Perturbations
JSON - learning notes (message converter, etc.)

论文阅读 (58):Research and Implementation of Global Path Planning for Unmanned Surface Vehicle Based...
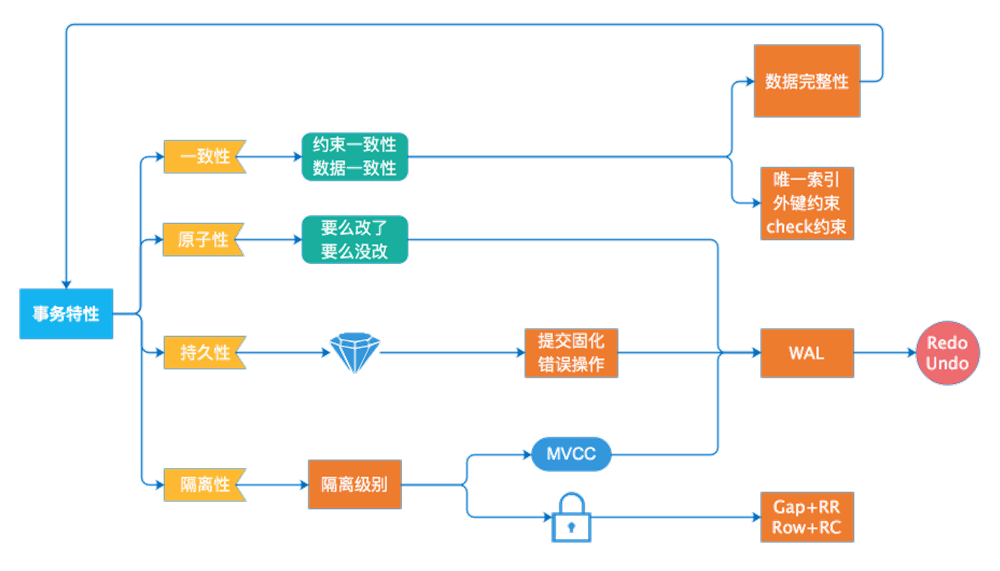
MySQL transaction and its characteristics and locking mechanism

Meituan Sanmian: how do you understand the principle of redis master-slave replication?

客服系统搭建教程_宝塔面板下安装使用方式_可对接公众号_支持APP/h5多租户运营...

org.apache.ibatis.binding.BindingException: Invalid bound statement (not found):...
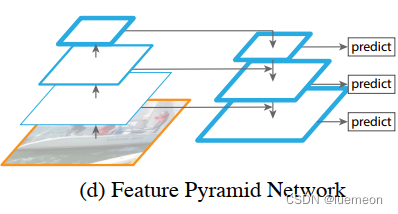
FPN characteristic pyramid network
随机推荐
Cryptography involved in IOT device end
Interpretation of eventbus source code
浅谈5类过零检测电路
JS custom error
Answer 02: why can Smith circle "allow left string and right parallel"?
CRMEB 二开短信功能教程
解答02:Smith圆为什么能“上感下容 左串右并”?
Tencent Qianfan scene connector: worry and effort saving automatic SMS sending
Answer 01: why can Smith circle "allow left string and right parallel"?
Kerberoasting without SPN
论文阅读 (50):A Novel Matrix Game with Payoffs of Maxitive Belief Structure
Analytic analog-to-digital (a/d) converter
手机开户一般哪个证券公司好?在线开户安全么?
MySQL的 安裝、配置、卸載
Explanation of the principle and code implementation analysis of rainbow docking istio
Installation, configuration, désinstallation de MySQL
Self supervised learning (SSL)
Company offensive operation guide
Easygbs playback screen is continuously loading. Troubleshooting
MySQL - reasons for using repeatable read