当前位置:网站首页>[combinatorics] exponential generating function (properties of exponential generating function | exponential generating function solving multiple set arrangement)
[combinatorics] exponential generating function (properties of exponential generating function | exponential generating function solving multiple set arrangement)
2022-07-03 18:18:00 【Programmer community】
List of articles
- One 、 Properties of exponential generating function
- Two 、 The exponential generating function solves the arrangement of multiple sets
Reference blog : Look in order
- 【 Combinatorial mathematics 】 Generating function Brief introduction ( Generating function definition | Newton's binomial coefficient | Common generating functions | Related to constants | Related to binomial coefficient | Related to polynomial coefficients )
- 【 Combinatorial mathematics 】 Generating function ( Linear properties | Product properties )
- 【 Combinatorial mathematics 】 Generating function ( Shift property )
- 【 Combinatorial mathematics 】 Generating function ( The nature of summation )
- 【 Combinatorial mathematics 】 Generating function ( Commutative properties | Derivative property | Integral properties )
- 【 Combinatorial mathematics 】 Generating function ( Summary of nature | Important generating functions ) *
- 【 Combinatorial mathematics 】 Generating function ( Generate function examples | Given the general term formula, find the generating function | Given the generating function, find the general term formula )
- 【 Combinatorial mathematics 】 Generating function ( Generate function application scenarios | Solving recursive equations using generating functions )
- 【 Combinatorial mathematics 】 Generating function ( Use the generating function to solve multiple sets r Combinatorial number )
- 【 Combinatorial mathematics 】 Generating function ( Use generating function to solve the number of solutions of indefinite equation )
- 【 Combinatorial mathematics 】 Generating function ( Examples of using generating functions to solve the number of solutions of indefinite equations )
- 【 Combinatorial mathematics 】 Generating function ( Examples of using generating functions to solve the number of solutions of indefinite equations 2 | Extended to integer solutions )
- 【 Combinatorial mathematics 】 Generating function ( Positive integer split | disorder | Orderly | Allow repetition | No repetition | Unordered and unrepeated splitting | Unordered repeated split )
- 【 Combinatorial mathematics 】 Generating function ( Positive integer split | Unordered non repeated split example )
- 【 Combinatorial mathematics 】 Generating function ( Positive integer split | Basic model of positive integer splitting | Disorderly splitting with restrictions )
- 【 Combinatorial mathematics 】 Generating function ( Positive integer split | Repeated ordered splitting | Do not repeat orderly splitting | Proof of the number of repeated ordered splitting schemes )
- 【 Combinatorial mathematics 】 Exponential generating function ( The concept of exponential generating function | Permutation number exponential generating function = General generating function of combinatorial number | Example of exponential generating function )
One 、 Properties of exponential generating function
Two sequences
{
a
n
}
,
{
b
n
}
\{a_n\} , \{b_n\}
{ an},{ bn} The corresponding exponential generating functions are
A
e
(
x
)
,
B
e
(
x
)
A_e(x) , B_e(x)
Ae(x),Be(x) ,
Put the above two Exponential generating function Multiply , As a function , It can be expanded into another series ,
A
e
(
x
)
⋅
B
e
(
x
)
=
∑
n
=
0
∞
c
n
x
n
n
!
A_e(x) \cdot B_e(x) = \sum\limits_{n=0}^{\infty} c_n \cfrac{x^n}{n!}
Ae(x)⋅Be(x)=n=0∑∞cnn!xn
among ,
c
n
=
∑
k
=
0
∞
(
n
k
)
a
k
b
n
−
k
c_n =\sum\limits_{k=0}^{\infty}\dbinom{n}{k}a_kb_{n-k}
cn=k=0∑∞(kn)akbn−k
( The result can be obtained by substituting )
Two 、 The exponential generating function solves the arrangement of multiple sets
Multiple sets
S
=
{
n
1
⋅
a
1
,
n
2
⋅
a
2
,
⋯
,
n
k
⋅
a
k
}
S=\{ n_1 \cdot a_1 , n_2 \cdot a_2 , \cdots , n_k \cdot a_k \}
S={ n1⋅a1,n2⋅a2,⋯,nk⋅ak}
Multiple sets
S
S
S Of
r
r
r Number of permutations Composition sequence
{
a
r
}
\{ a_r \}
{ ar} , The corresponding exponential generating function is :
G
e
(
x
)
=
f
n
1
(
x
)
f
n
2
(
x
)
⋯
f
n
k
(
x
)
G_e(x) = f_{n_1}(x) f_{n_2}(x) \cdots f_{n_k}(x)
Ge(x)=fn1(x)fn2(x)⋯fnk(x) *
Each generated function item
f
n
i
(
x
)
f_{n_i}(x)
fni(x) yes
f
n
i
(
x
)
=
1
+
x
+
x
2
2
!
+
⋯
+
x
n
i
n
i
!
f_{n_i}(x) = 1 + x + \cfrac{x^2}{2!} + \cdots + \cfrac{x^{n_i}}{n_i!}
fni(x)=1+x+2!x2+⋯+ni!xni *
take
G
e
(
x
)
G_e(x)
Ge(x) an , Among them
x
r
r
!
\cfrac{x^r}{r!}
r!xr The coefficient of is the permutation number of multiple sets , Pay special attention if not
x
r
r
!
\cfrac{x^r}{r!}
r!xr form , It needs to be forcibly transformed into the above properties , Be sure to divide by
r
!
r!
r! ; *****
Select the problem reference :
n
n
n Meta set
S
S
S , from
S
S
S Select... From the set
r
r
r Elements ;
according to Whether the element can be repeated , Whether the selection process is orderly , The selection question is divided into four sub types :
| Elements do not repeat | Elements can be repeated | |
|---|---|---|
| Orderly selection | Set arrangement P ( n , r ) P(n,r) P(n,r) | Multiset arrangement |
| Unordered selection | Set combination C ( n , r ) C(n,r) C(n,r) | Combination of multiple sets |
Select the question :
- Non repeatable elements , Orderly selection , Corresponding Arrangement of sets ;
P
(
n
,
r
)
=
n
!
(
n
−
r
)
!
P(n,r) = \dfrac{n!}{(n-r)!}
P(n,r)=(n−r)!n!
- Non repeatable elements , Unordered selection , Corresponding A combination of sets ;
C
(
n
,
r
)
=
P
(
n
,
r
)
r
!
=
n
!
r
!
(
n
−
r
)
!
C(n,r) = \dfrac{P(n,r)}{r!} = \dfrac{n!}{r!(n-r)!}
C(n,r)=r!P(n,r)=r!(n−r)!n!
- Repeatable elements , Orderly selection , Corresponding Arrangement of multiple sets ;
whole
row
Column
=
n
!
n
1
!
n
2
!
⋯
n
k
!
Full Permutation = \cfrac{n!}{n_1! n_2! \cdots n_k!}
whole row Column =n1!n2!⋯nk!n! , Incomplete permutation
k
r
,
r
≤
n
i
k^r , \ \ r\leq n_i
kr, r≤ni
- Repeatable elements , Unordered selection , Corresponding Combination of multiple sets ;
N
=
C
(
k
+
r
−
1
,
r
)
N= C(k + r - 1, r)
N=C(k+r−1,r)
边栏推荐
- Win 11 major updates, new features love love.
- Win32: analyse du fichier dump pour la défaillance du tas
- MySQL grouping query
- Change the single node of Postgres database into master-slave
- Codeforces Round #803 (Div. 2) C. 3SUM Closure
- SQL injection -day16
- Self executing function
- Fedora 21 安装 LAMP 主机服务器
- Redis on local access server
- How to deploy applications on kubernetes cluster
猜你喜欢

Sensor debugging process

Computer graduation design PHP sports goods online sales system website
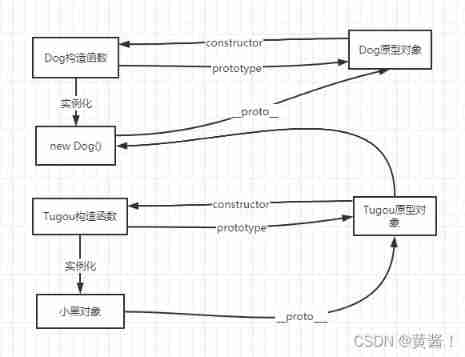
Prototype inheritance..

基于人脸识别的课堂考勤系统 tkinter+openpyxl+face_recognition
AcWing 271. 杨老师的照相排列【多维DP】

PHP MySQL inserts multiple pieces of data
![[combinatorics] generating function (summation property)](/img/74/e6ef8ee69ed07d62df9f213c015f2c.jpg)
[combinatorics] generating function (summation property)

SQL injection -day16
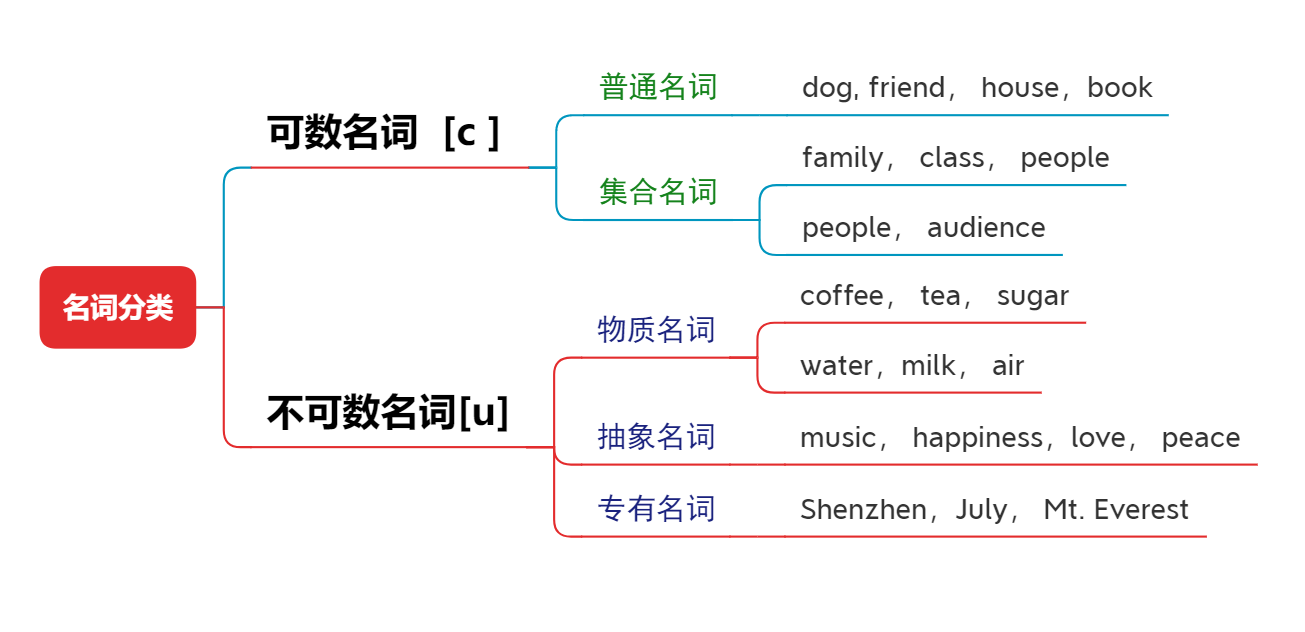
Grammaire anglaise Nom - Classification
Naoqi robot summary 27
随机推荐
webcodecs
Redis core technology and practice - learning notes (IX): slicing cluster
Kotlin的協程:上下文
SQL injection -day16
Research Report on competitive strategy Outlook Analysis and investment strategic planning of China's smart home equipment industry, 2022-2028
win32:堆破坏的dump文件分析
统计图像中各像素值的数量
Postfix 技巧和故障排除命令
Ml (machine learning) softmax function to realize the classification of simple movie categories
English grammar_ Noun classification
Global and Chinese health care OEM and ODM market status survey and investment planning recommendations report 2022-2028
Prototype inheritance..
Research on Swift
Talk about the design and implementation logic of payment process
Summary and Reflection on the third week of winter vacation
[combinatorics] exponential generating function (concept of exponential generating function | permutation number exponential generating function = combinatorial number ordinary generating function | e
[combinatorics] generating function (positive integer splitting | basic model of positive integer splitting | disordered splitting with restrictions)
Analysis report on production and marketing demand and investment forecast of China's PVC industry from 2021 to 2026
Five problems of database operation in commodity supermarket system
How to draw non overlapping bubble chart in MATLAB