当前位置:网站首页>学习笔记-----左偏树
学习笔记-----左偏树
2022-08-05 02:00:00 【Oops_Corsini】
真左偏树:

忽略忽略
下边才是(图源百度):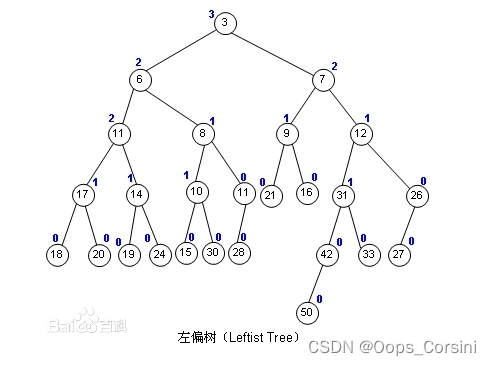
概念:
左偏树是是一颗具有堆性质的二叉树。属于可并堆。
它的节点除了和二叉树的节点一样具有左右子树的指针 ( l i g h t , r i g h t ) (light,right) (light,right)外,话有两个性质:键值和距离 ( d i s t ) (dist) (dist)。
键值用于比较节点的大小
距离定义: 当且仅当节点 i i i的左子树和右子树为空树的时候,节点被称作外节点,节点的距离是节点 i i i到它的后代中的距离最近的外节点的边数。特别的,如果节点 i i i本身就是外节点,则它的距离为0;而空节点的距离视为 − 1 -1 −1
性质
节点的键值小于或等于它的左右子节点的键值
节点的左节点的距离不小于右子节点的距离
推论
节点的距离等于它的右子节点的距离+1
一棵 N N N个节点的左偏树 r o o t root root节点的距离最多为 l o g ( N + 1 ) − 1 log(N+1)-1 log(N+1)−1
证明: 左偏树根节点的距离一定,那么节点最少的情况下就是一棵完全二叉树,节点数是 2 d + 1 − 1 2^{d+1}-1 2d+1−1,那么 n n n个节点的左偏树的距离也就 ≤ l o g ( n + 1 ) − 1 \leq log(n+1)-1 ≤log(n+1)−1.
这也是左偏树时间复杂度的保证。
合并操作
合并操作是左偏树最基本的操作。merge打天下!!
左偏树增加一个节点,删除根节点,初始化一批数据都是基于合并操作。
假设我们现在合并 x x x和 y y y两棵树
比较两棵树值的大小,假设 x . v a l < y . v a l x.val < y.val x.val<y.val
将值小的节点 ( x ) (x) (x)作为根节点,递归合并 x x x的右子树和 y y y
若合并后不满足左偏性质,交换左右子树
当 x x x的右子树或 y y y为空时合并结束
图解(自己画的造的 树比较垃圾):
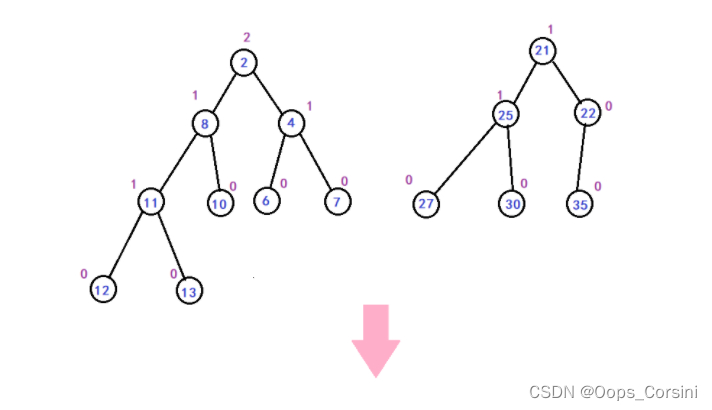
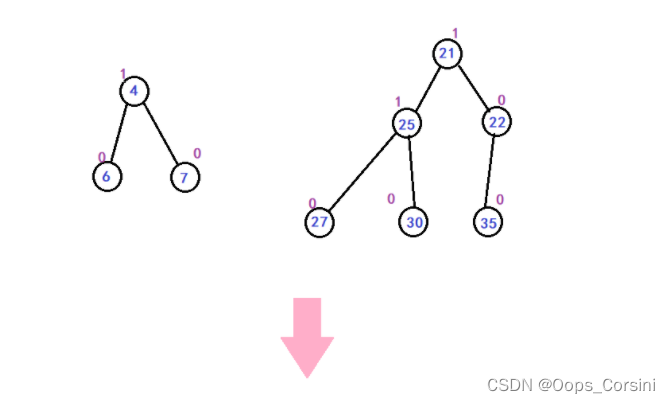
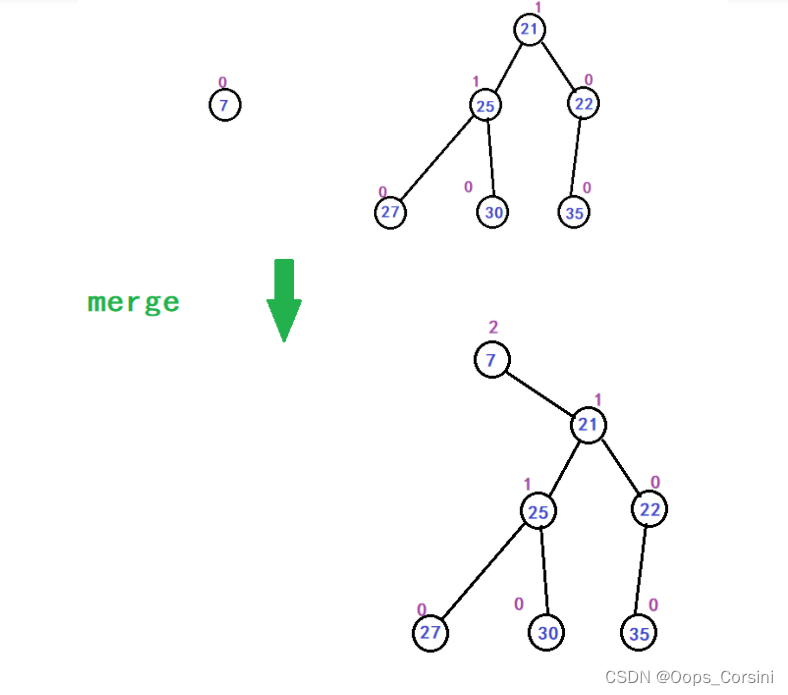
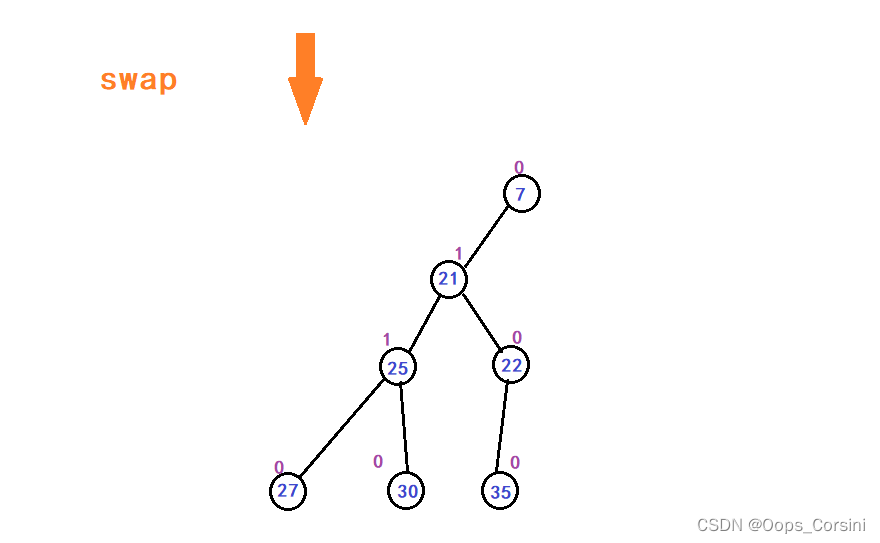
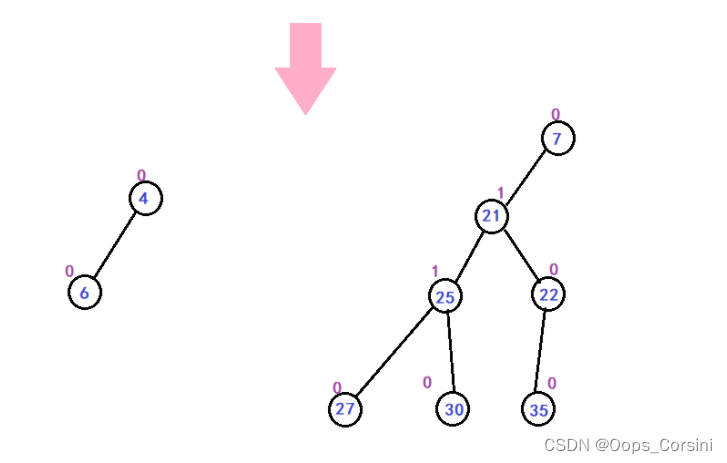
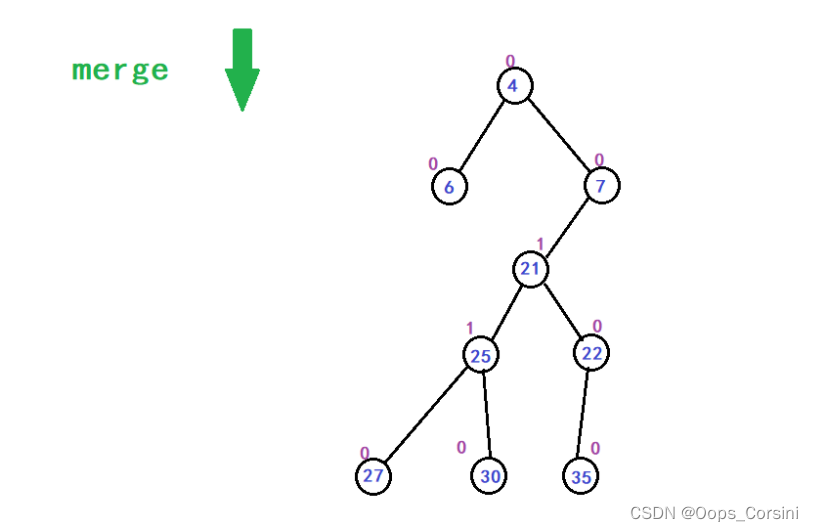
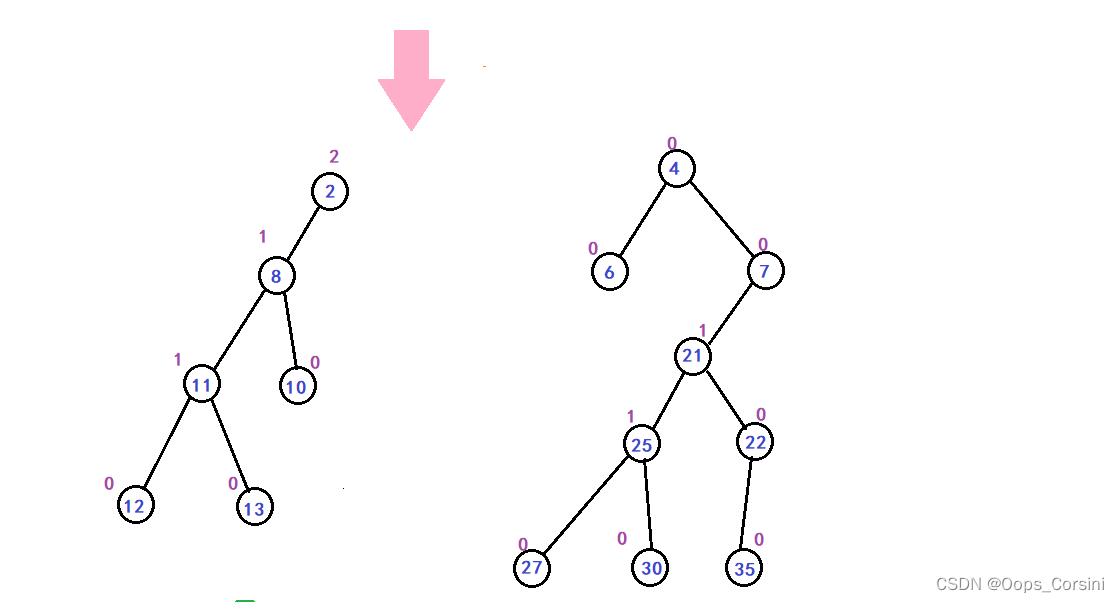
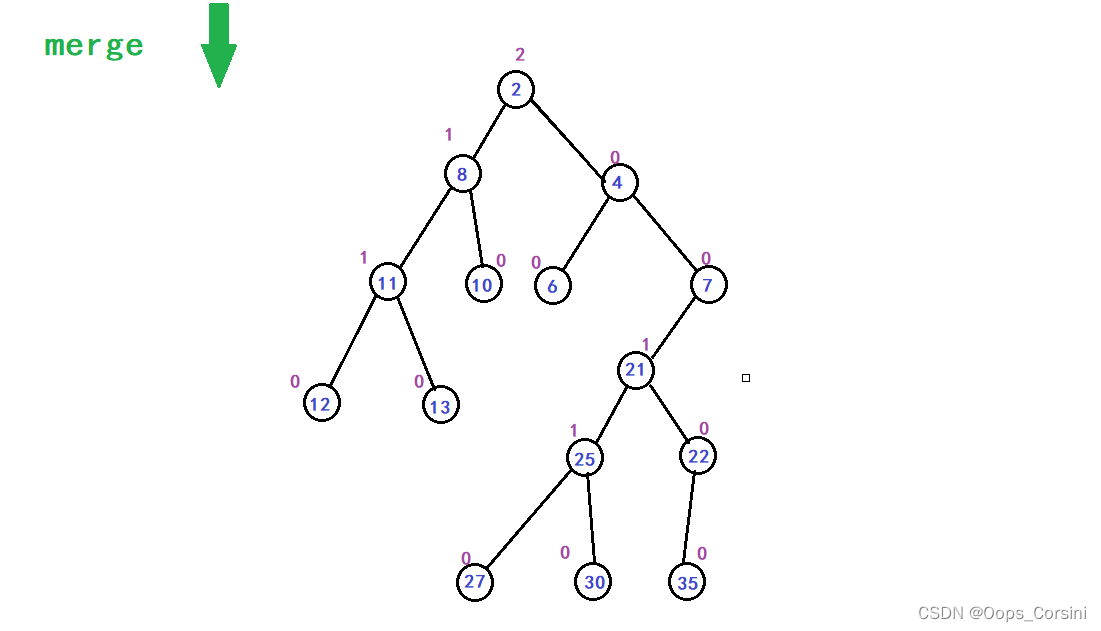
动图(图源洛谷):
code
int merge(int x,int y){
if(!x||!y)return x+y;
if(e[x].val>e[y].val)swap(x,y);//保证x的val比y的小
e[x].r=merge(e[x].r,y);
if(e[e[x].r].dist>e[e[x].l].dist)swap(e[x].l,e[x].r)//不满足左偏性质,交换左右子树
e[x].dist=e[e[x].r].dist+1;
return x;//返回root
}
其它操作
插入
把一个节点看作一个堆进行合并操作.
时间复杂度是 O ( l o g n ) O(logn) O(logn)
删除
删堆顶:
把堆顶的左右儿子合并,并处理一下信息
任意元素:
首先合并左右儿子,再把左右儿子形成的新堆合并到删除元素的父亲上.
还需要自底向上更新 d i s t dist dist,不满足左偏性质时交换左右儿子
构建左偏树
只会操作也不行,还要会构建树,没有树你在哪里操作??
这也算一个常用操作
方法一
逐个插入法:
将只有一个节点的左偏树逐个合并进去。
复杂度: O ( l o g 1 ) + O ( l o g 2 ) + . . . + O ( l o g n ) = O ( n l o g n ) O(log1)+O(log2)+...+O(logn)=O(nlogn) O(log1)+O(log2)+...+O(logn)=O(nlogn)
方法二
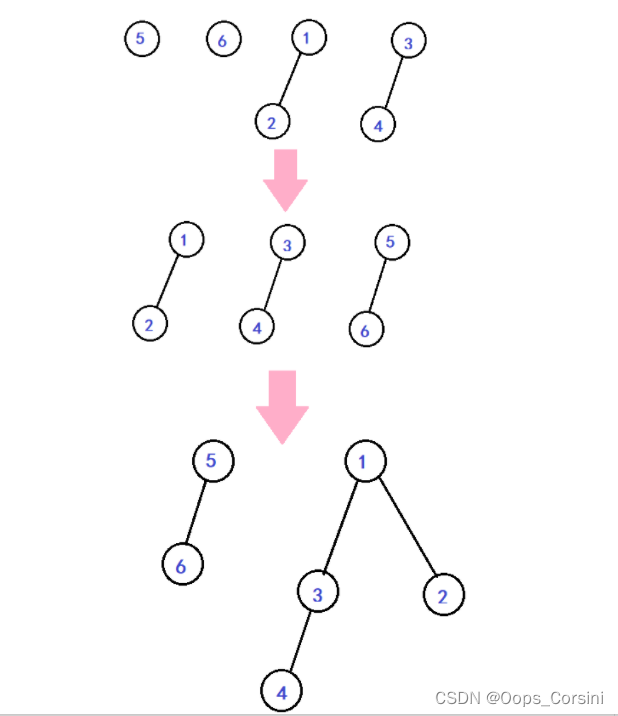
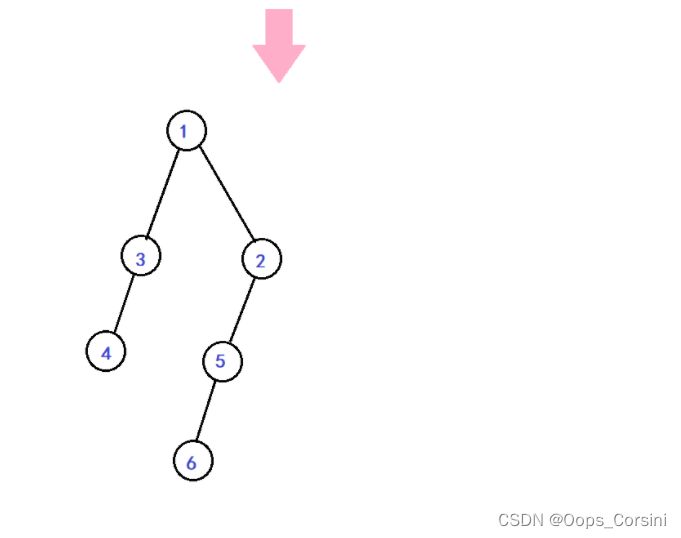
合并法:
仿照二叉堆的构建算法得到:
过程:
将 n n n个节点(每个节点看作一棵左偏树)放进先进先出的优先队列
不断地从队首取出两棵左偏树,合并之后再加入队尾
当队列只剩下一颗左偏树时,算法结束
时间复杂度: O ( n ) O(n) O(n)
水图:
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-ux49r2SW-1659532605333)(file://C:\Users\Administrator\AppData\Roaming\marktext\images\2022-08-03-17-36-58-image.png?msec=1659519418977)]](/img/3d/86b0762c66940f067446aa6802db60.png)
例题
例题代码里都忘记了加e[0].dist=-1,但是都水过了
知道遇到了城池占领。。。。。
1.
寻找根节点可以采用并查集的思想,用路径压缩的方式求一个节点的根节点;
v i s vis vis判断是否被删除
Code
#include<bits/stdc++.h>
#define maxn 1000010
using namespace std;
int n,rt[maxn],m;
struct node{
int val,l,r,dist;
}e[maxn];
bool vis[maxn];
int find(int x){
if(rt[x]==x)return x;
else return rt[x]=find(rt[x]);
}
int merge(int x,int y){
if(!x||!y)return x+y;
if(e[x].val>e[y].val)swap(x,y);
e[x].r=merge(e[x].r,y);
if(e[e[x].r].dist>e[e[x].l].dist)swap(e[x].l,e[x].r);
e[x].dist=e[e[x].r].dist+1;
return x;
}
int main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++){
scanf("%d",&e[i].val);
rt[i]=i;
}
for(int opt,x,y,i=1;i<=m;i++){
scanf("%d%d",&opt,&x);
if(opt==1){
scanf("%d",&y);
if(vis[x]||vis[y])continue;
int fx=find(x);
int fy=find(y);
int c;
if(fx!=fy)c=rt[fx]=rt[fy]=merge(fx,fy);
}
else{
if(vis[x]){
puts("-1");continue;
}
int fx=find(x);
printf("%d\n",e[fx].val);
vis[fx]=1;
rt[fx]=rt[e
[fx].l]=rt[e[fx].r]=merge(e[fx].l,e[fx].r);
//rt[fx]也要赋值是因为可能路径压缩是存在节点的rt等于x,但是x已经删除,所以要指向新节点
e[fx].l=e[fx].r=e[fx].dist=0;
}
}
return 0;
}
2.
和模板几乎一模一样
#include<bits/stdc++.h>
#define maxn 1000010
using namespace std;
int n,m,rt[maxn];
struct node{
int l,r,dist,val;
}e[maxn];
bool vis[maxn];
int find(int x){
return rt[x]==x?x:rt[x]=find(rt[x]);
}
int merge(int x,int y){
if(!x||!y)return x+y;
if(e[x].val>e[y].val)swap(x,y);
e[x].r=merge(e[x].r,y);
if(e[e[x].r].dist>e[e[x].l].dist)swap(e[x].l,e[x].r);
e[x].dist=e[e[x].r].dist+1;
return x;
}
int main(){
scanf("%d",&n);
for(int i=1;i<=n;i++){
scanf("%d",&e[i].val);
rt[i]=i;
}
scanf("%d",&m);
for(int x,y,i=1;i<=m;i++){
char opt;
cin>>opt;
if(opt=='M'){
scanf("%d%d",&x,&y);
if(vis[x]||vis[y])continue;
int fx=find(x);
int fy=find(y);
if(fx!=fy)rt[fx]=rt[fy]=merge(fx,fy);
}
else {
scanf("%d",&x);
if(vis[x]){
puts("0");continue;
}
int fx=find(x);
printf("%d\n",e[fx].val);
vis[fx]=1;
rt[fx]=rt[e[fx].l]=rt[e[fx].r]=merge(e[fx].l,e[fx].r);
e[fx].l=e[fx].r=e[fx].dist=0;
}
}
return 0;
}
3.
这题是大根堆。。。
#include<bits/stdc++.h>
#define maxn 1000010
using namespace std;
int n,m,rt[maxn];
struct node{
int l,r,dist,val;
}e[maxn];
int find(int x){
if(rt[x]==x)return x;
else return rt[x]=find(rt[x]);
}
int merge(int x,int y){
if(!x||!y)return x+y;
if(e[x].val<e[y].val)swap(x,y);
e[x].r=merge(e[x].r,y);
if(e[e[x].l].dist<e[e[x].r].dist)swap(e[x].l,e[x].r);
e[x].dist=e[e[x].r].dist+1;
return x;
}
int weak(int x){
e[x].val>>=1;
int rot=merge(e[x].l,e[x].r);
e[x].l=e[x].r=e[x].dist=0;
return rt[rot]=rt[x]=merge(rot,x);
}
int main(){
while(~scanf("%d",&n)){
for(int i=1;i<=n;i++){
e[i].l=e[i].r=e[i].dist=0;
scanf("%d",&e[i].val);
rt[i]=i;
}
scanf("%d",&m);
for(int x,y,i=1;i<=m;i++){
scanf("%d%d",&x,&y);
int fx=find(x);
int fy=find(y);
if(fx==fy){
puts("-1");continue;
}
int xx=weak(fx),yy=weak(fy);
rt[xx]=rt[yy]=merge(xx,yy);
printf("%d\n",e[rt[xx]].val);
}
}
return 0;
}
4.
5.
边栏推荐
- CMS建站流程
- 【MySQL series】- Does LIKE query start with % will make the index invalid?
- 刷爆朋友圈,Alibaba出品亿级并发设计速成笔记太香了
- Method Overriding and Object Class
- 转:查尔斯·汉迪:你是谁,比你做什么更重要
- 高数_复习_第1章:函数、极限、连续
- 行业现状?互联网公司为什么宁愿花20k招人,也不愿涨薪留住老员工~
- Transfer Learning - Distant Domain Transfer Learning
- "Configuration" is a double-edged sword, it will take you to understand various configuration methods
- C语言基础知识 -- 指针
猜你喜欢
Why is this problem reported when installing oracle11

Hypervisor related knowledge points
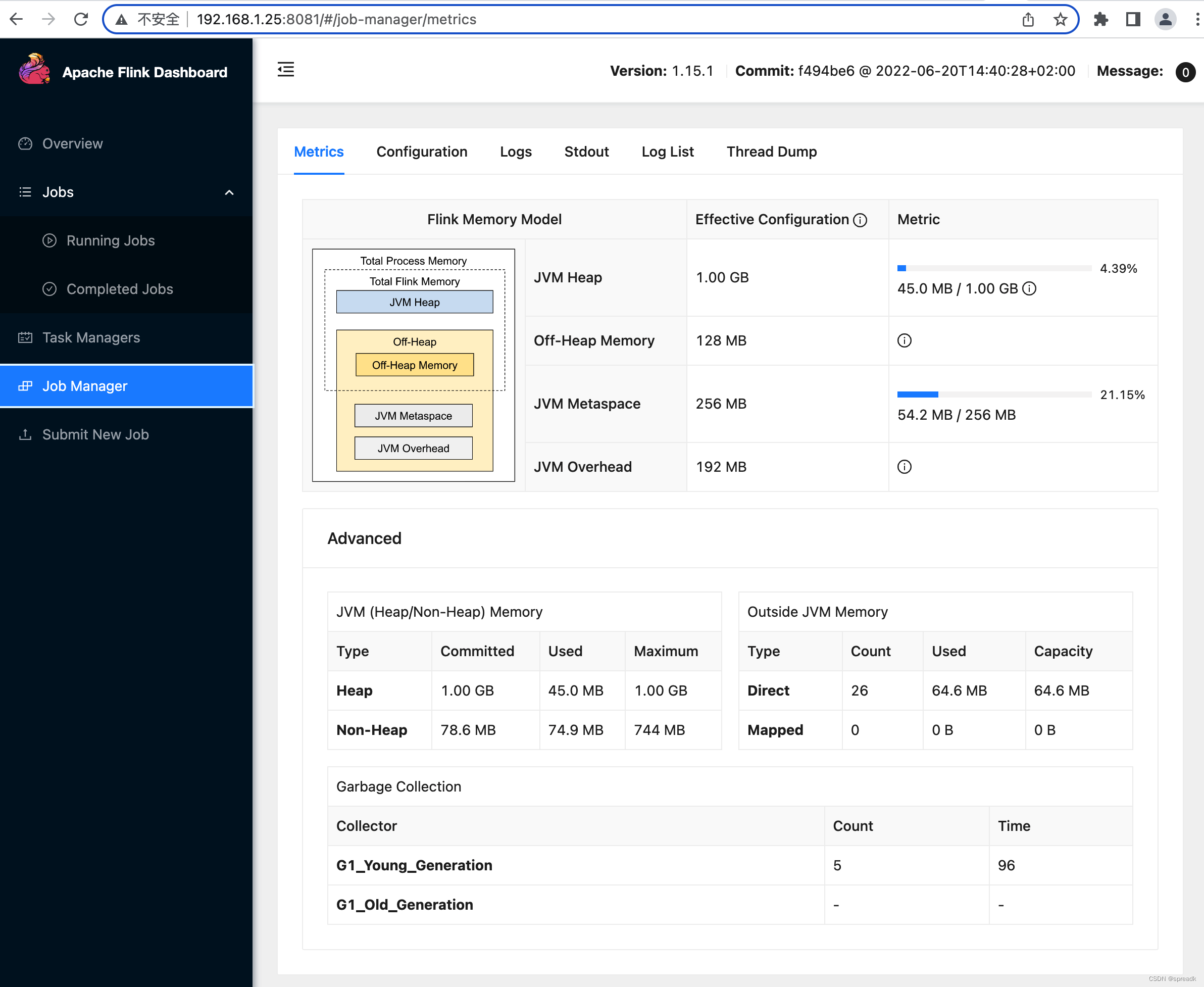
Flink 1.15.1 集群搭建(StandaloneSession)
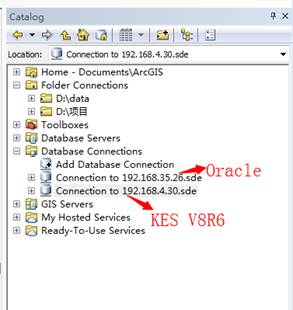
金仓数据库 KingbaseES V8 GIS数据迁移方案(3. 基于ArcGIS平台的数据迁移到KES)

HOG feature study notes

使用SuperMap iDesktopX数据迁移工具迁移地图文档和符号

iNFTnews | What can NFTs bring to the sports industry and fans?
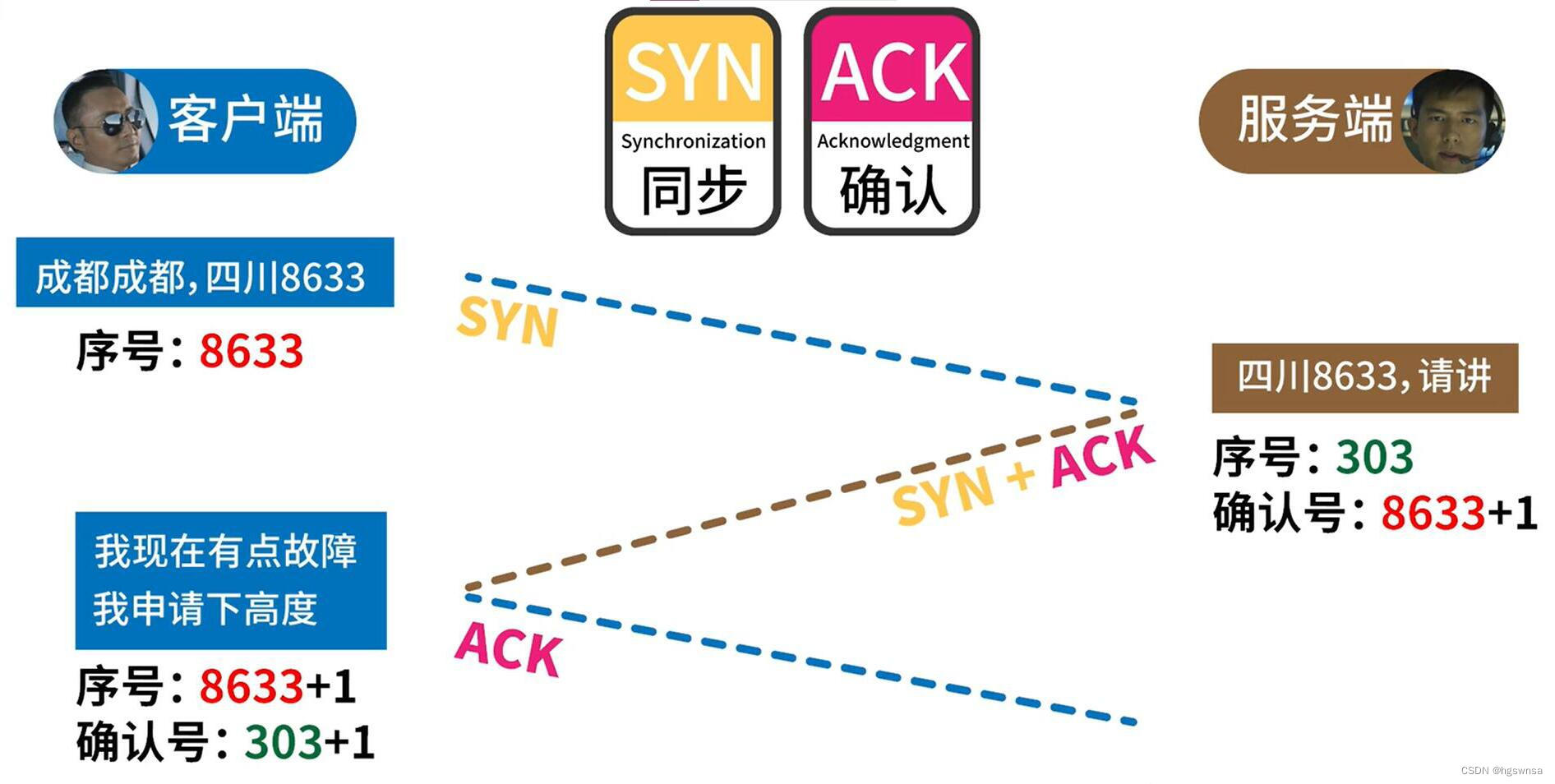
Three handshake and four wave in tcp
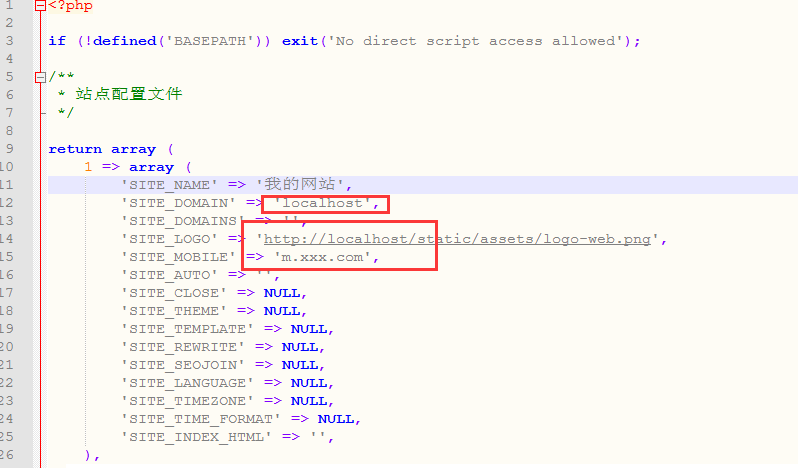
Xunrui cms website cannot be displayed normally after relocation and server change
KingbaseES V8 GIS data migration solution (2. Introduction to the capabilities of Kingbase GIS)
随机推荐
Transfer Learning - Distant Domain Transfer Learning
Transfer Learning - Joint Geometrical and Statistical Alignment for Visual Domain Adaptation
Are testing jobs so hard to find?I am 32 this year and I have been unemployed for 2 months. What should an older test engineer do next to support his family?
LPQ(局部相位量化)学习笔记
LPQ (local phase quantization) study notes
Day Fourteen & Postman
【日常训练】1403. 非递增顺序的最小子序列
Use of pytorch: Convolutional Neural Network Module
迁移学习——Joint Geometrical and Statistical Alignment for Visual Domain Adaptation
如何创建rpm包
[Word] #() error occurs after Word formula is exported to PDF
Leetcode刷题——22. 括号生成
CPDA|运营人如何从负基础学会数据分析(SQL)
网络安全与元宇宙:找出薄弱环节
【Redis】Linux下Redis安装
STM32使用stm32cubemx LL库系列教程
sql语句多字段多个值如何进行排序
超越YOLO5-Face | YOLO-FaceV2正式开源Trick+学术点拉满
<开发>实用工具
Why is this problem reported when installing oracle11