当前位置：网站首页>Seven sorting details

Sort , Is to make a string of records , According to the size of one or some of the keywords , An operation arranged in ascending or descending order . In the usual context , If it comes to sorting , It's usually in ascending order ( Non descending order ). Sort in the usual sense , They all mean sort in place (in place sort).

2、 Stability of sequencing

In the sequence to be sorted , There are elements with the same value , After sorting , The sorting algorithm whose order of values is equal and does not change is called a stable algorithm . It's in the picture below 5a and 5b The order of has not changed .

3、 Internal sort and external sort

（1） Internal sorting

The data to be sorted is placed in memory

（2） External sorting

Data is stored on the hard disk , Each sorting needs to read part of the contents from the hard disk to the memory , Sort this part of data before writing it to the hard disk . For example, bucket sorting , Radix sorting , Odd sort , These methods can only be used in special situations , Limited .

Two 、 Test methods for major sorting

package Seven_sorts;

import java.lang.reflect.Method;
import java.util.Arrays;
import java.util.concurrent.ThreadLocalRandom;

/**
 *  Test seven sorts 
 */
public class SortTest {
    // A class that generates random numbers 
    private static final ThreadLocalRandom random=ThreadLocalRandom.current();

    /**
     *  Produce a size of n Array of random integers , The value range of the array is [l...r]
     * @param n   The number of elements in the array 
     * @param l   The minimum value of the array 
     * @param r   The maximum value of the array 
     * @return
     */
    public static int[] generaRabdomArrary(int n,int l,int r){
        int[] data=new int[n];
        for (int i = 0; i <n ; i++) {
            // It generates a [l...r) The random number of is placed in the array 
            data[i]= random.nextInt(l,r);
        }
        return data;
    }

    /**
     *  Generate a size of n An almost ordered array of 
     * @param n   Element number 
     * @param swaptinmes   The number of exchanges , The more times , The more unordered the array 
     * @return
     */
    public static int[] generateSortArrary(int n,int swaptinmes){
        // Sir into an ordered array 
        int[] data =new int[n];
        for (int i = 0; i < n; i++) {
            data[i]=i;
        }
        // Exchange some elements of an ordered array 
        for (int i = 0; i <swaptinmes; i++) {
            int a= random.nextInt(n);
            int b= random.nextInt(n);
            int temp=data[a];
            data[a]=data[b];
            data[b]=temp;
        }
        return data;
    }

    /**
     *  Deep copy array 
     * @param arr
     * @return
     */
    public static int[] arraryCopy(int[] arr){
        return Arrays.copyOf(arr,arr.length);
    }

    /**
     *  In the specified array arr The name of the last test is sortName Sorting time of 
     * @param arr
     * @param sortName
     */
    public static void testSort(int[] arr,String sortName){
        Class<SevenSort> cla=SevenSort.class;
        try {
            // Get the algorithm according to the name of the tactics 
            Method method= cla.getDeclaredMethod(sortName,int[].class);
            // timing 
            long start=System.nanoTime();
            method.invoke(null,arr);
            long end=System.nanoTime();
            if (isSorted(arr)){
                System.out.println(sortName+" Sort complete , Total time consuming ："+(end-start)/1000000.0+"ms");
            }
        }catch (Exception e){
            e.printStackTrace();
        }
    }

    /**
     *  Check whether the current array is a non descending array 
     * @param arr
     * @return
     */
    private static boolean isSorted(int[] arr){
        for (int i = 0; i < arr.length-1; i++) {
            if (arr[i]>arr[i+1]){
                System.out.println(" The sorting algorithm is wrong ！");
                return false;
            }
        }
        return true;
    }
}

3、 ... and 、 Selection sort

1、 Direct selection sorting

Each time, the largest... Is selected from the unordered interval （ Or the smallest ） An element of , At the end of the unordered interval （ Or first ）, Until all the data elements to be sorted are finished .

Insert picture description here

9,2,5a,7,5b,4,3,6
For this set of data , At the beginning of sorting ,
Sorted array （ Disordered interval ） by [i...n), Sorted array （ Ordered interval ） by []
After the first sorting ,2,9,5a,7,5b,4,3,6
Sorted array （ Disordered interval ） by [i...n)-1, Sorted array （ Ordered interval ） by []+1

 /**
     *  Direct selection sorting 
     * @param arr
     */
    public static void selsctionSort(int[] arr){
        // The initial unordered interval [i...n), The ordered interval is []
        for (int i = 0; i < arr.length; i++) {
            // Minimum element index subscript 
            int min=i;
            for (int j = i+1; j < arr.length; j++) {
                if (arr[j]<arr[min]){
                    min=j;
                }
            }
            // here min Is the index of the minimum value , Exchange operations 
            swap(arr,i,min);
        }
    }

2、 Heap sort

CSDNhttps://mp.csdn.net/mp_blog/creation/editor/124864506

3、 Bidirectional selection sorting

Optimize direct selection sorting , Select the maximum and minimum values at the same time

/**
     *  Bidirectional selection sorting 
     * @param arr
     */
    public static void selectionSortOP(int[] arr){
        int low=0;
        int high= arr.length-1;
        // Cycle termination conditions , When low==high when , The unordered interval leaves only the last element , At this point, the array has been ordered 
        while (low<high){
            int min=low;
            int max=low;
            for (int i = low+1; i <=high; i++) {
                if (arr[i]<arr[min]){
                    min=i;
                }
                if (arr[i]>arr[max]){
                    max=i;
                }
            }
            // here min Corresponds to the minimum index , Swap to the front of the unordered interval 
            swap(arr,min,low);
            // Pay attention to consider when low==max The situation of 
            if (low==max){
                max=min;
            }
            swap(arr,max,high);
            low++;
            high--;
        }
    }

Four 、 Exchange sort

（1） Bubble sort

CSDNhttps://mp.csdn.net/mp_blog/creation/editor/124098197 Bubble sorting diagram demonstration ( This is from the Internet )

 /**
     *  Bubble sort 
     * @param arr
     */
    public static void bubbleSort(int[] arr){
        for (int i = 0; i < arr.length-1 ; i++) {
            boolean isSSwapped=false;
            for (int j = 0; j < arr.length-i-1 ; j++) {
                if (arr[j]>arr[j+1]){
                    swap(arr,j,j+1);
                    isSSwapped=true;
                }
            }
            if (!isSSwapped){
                break;
            }
        }
    }

2、 Quick sort

Quick sort ,20 One of the greatest algorithms of the th century , The core idea is zoning
Select a value in the unordered interval as the dividing point pivot, Start scanning collection , All in the array are less than pivot The element of is placed on the left side of the dividing point , Will be greater than or equal to pivot The element of is placed on the right side of the dividing point , After this round of exchange ,pivot In the final position , Then repeat the above process in two sub intervals , Until the whole combination is in order .

（1） Partition method 1

When arrays are nearly ordered , The performance degradation of quick sort is very serious , In extreme cases , Suppose the array is almost ordered , When partitioning according to the leftmost element , It will cause extreme imbalance between the two recursive subtrees in the recursive process , It will even degenerate into a linked list . The solution is to select any element in the array as the partition point for each recursion .

/**
     *  Quick sort 
     * @param arr
     */
    public static void quickSort(int[] arr){
        quickSortInternal(arr,0,arr.length-1);
    }

    private static void quickSortInternal(int[] arr, int l, int r) {
//        // Optimize 2
//        if (r-l<=15){
//            insertionSort(arr,l,r);
//            return;
//        }
        if (l>=r){
            return;
        }
        int p=partion(arr,l,r);
        // Continue to sort quickly in two subintervals 
        // Less than v The elements of 
        quickSortInternal(arr,l,p-1);
        // Greater than v The elements of 
        quickSortInternal(arr,p+1,r);
    }

    /**
     * Partition method 
     * @param arr
     * @param l
     * @param r
     * @return
     */
    private static int partion(int[] arr, int l, int r) {
//        // Optimize 1
//        int randomIndex=random.nextInt(l,r);
//        swap(arr,l,randomIndex);
        int v=arr[l];
        //arr[l+1...j] Time is less than v The range of , At first, this interval has no elements 
        int j=l;
        //arr[j+1...i] Time greater than v The range of , At first, this interval also has no elements 
        for (int i = l+1; i <=r ; i++) {
            if (arr[i]<v){
                swap(arr,i,j+1);
                j++;
            }
        }
        // This element j It's the last one <v The elements of , Just put v Exchange to j The location of 
        swap(arr,l,j);
        return j;
    }

（2） Partition method 2

 /**
     *  Quick sort digging 
     * @param arr
     */
    public static void quickSortHoare(int[] arr){
        quickSortHoareInternal(arr,0,arr.length-1);
    }

    private static void quickSortHoareInternal(int[] arr, int l, int r) {
        //        // Optimize 2
//        if (r-l<=15){
//            insertionSort(arr,l,r);
//            return;
//        }
        if (l>=r){
            return;
        }
        int p=partitionHoare(arr,l,r);
        // Continue to sort quickly in two subintervals 
        // Less than v The elements of 
        quickSortHoareInternal(arr,l,p-1);
        // Greater than v The elements of 
        quickSortHoareInternal(arr,p+1,r);
    }

    /**
     *  Zoning method II excavation method 
     * @param arr
     * @param l
     * @param r
     * @return
     */
    private static int partitionHoare(int[] arr, int l, int r) {
        int randomIndex=random.nextInt(l,r);
        swap(arr,l,randomIndex);
        int pivot=arr[l];
        int i=l;
        int j=r;
        while (i<j){
            // First, let j Go forward from the back to the first one less than v The element of stops 
            while(i<j&&arr[j]>=pivot){
                j--;
            }
            arr[i]=arr[j];
            // Then let's i Walk from front to back to the first greater than v The elements of 
            while (i<j&&arr[i]<=pivot){
                i++;
            }
            arr[j]=arr[i];
        }
        arr[i]=pivot;
        return i;
    }

5、 ... and 、 Insertion sort

1、 Direct insert sort

Select the first element of the unordered interval each time , Insert at the right position in the ordered interval

Insert picture description here

  /**
     *  Direct insert sort 
     * @param arr
     */
    public static void insertionSort(int[] arr){
        for (int i = 1; i < arr.length ; i++) {
            // Ordered interval [0..1) By default, the first element is ordered , The interval to be sorted [i...n)
            // Select the first element of the first interval of the unordered interval , Keep looking forward, choose a position to put 
//            for (int j = i; j >=1&&arr[j]<arr[j-1]; j--) {
//                swap(arr,j,j-1);
//            }
            for (int j = i; j >=1; j--) {
                if (arr[j]>arr[j-1]){
                    //arr[i] It happens to be the last element of the ordered interval , The first element of an unordered interval 
                    break;
                }else {
                    swap(arr,j,j-1);
                }
            }
        }
    }

2、 Binary Insertion Sort

The principle of half insertion sort algorithm is the same as that of direct insertion sort algorithm . It's just , When inserting data into sorted data , Use to half find （ Two points search ）. Take the middle element of the sorted sequence first , Compare with the data to be inserted , If the value of the intermediate element is greater than the data to be inserted , Then the data to be inserted belongs to the first half of the array , Otherwise, it belongs to the second half . By analogy , Keep narrowing down , Determine where to insert .


    /**
     *  Binary Insertion Sort 
     * @param arr
     */
    public static void insertionSortBS(int[] arr){
        // Ordered interval [0...i) Disordered interval [i...n)
        for (int i = 0; i < arr.length; i++) {
            int val=arr[i];
            // Ordered interval [left...right]
            int left=0;
            int right=i;
            while (left<right){
                int mid=(left+right)/2;
                if (val<arr[mid]){
                    right=mid;
                }else {
                    left=mid+1;
                }
            }
            // Move [left...i) The elements of 
            for (int j = i; j >left; j--) {
                arr[j]=arr[j-1];
            }
            //left Is the position to be inserted 
            arr[left]=val;
        }
    }

3、 Shell Sort

When the array is close to order , The efficiency of insertion sorting is very high , Hill sorting is constantly adjusting the small array in order , Until the whole large array is close to order , At this time, use insert sorting again , Efficiency will be greatly improved .
① Choose an integer first gap, Divide the array to be sorted into gap Group , All distances are gap Is the same group ,, First, insert and sort each small array .
② Give Way gap=gap/2(3), Repeat the first step
③ When gap=1 when , At this point, it shows that the entire array has been adjusted to be almost orderly , You only need to insert and sort again , In this way, the efficiency will be improved a lot .

/**
     *  Shell Sort 
     * @param arr
     */
    public static void shellSort(int[] arr){
        int gap= arr.length/2;
        // Step one, step two 
        while (gap>1){
           insertionSortGap(arr,gap);
           gap=gap/2;
        }
        // When gap be equal to 1 when , The whole large array is almost orderly , At this point, insert the sort again 
        insertionSort(arr);
    }
    /**
     * Insert sorted 1 Replace with gap This is the insertion sort here 
     * @param arr
     * @param gap
     */
    private static void insertionSortGap(int[] arr, int gap) {
        for (int i =gap; i < arr.length; i++) {
            for (int j = i; j-gap >=0&&arr[i]<arr[j-gap] ; j--) {
                swap(arr,j,j-gap);
            }
        }
    }

6、 ... and 、 Merge sort

return ： Keep dividing the original array into sub arrays ( Split in two ), Until there is only one element left in each array , The return process is over
and ： Continue to combine two adjacent words into a large array , The merging process is to merge the ordered subarray into a large ordered subarray , Until it is merged into the whole array .

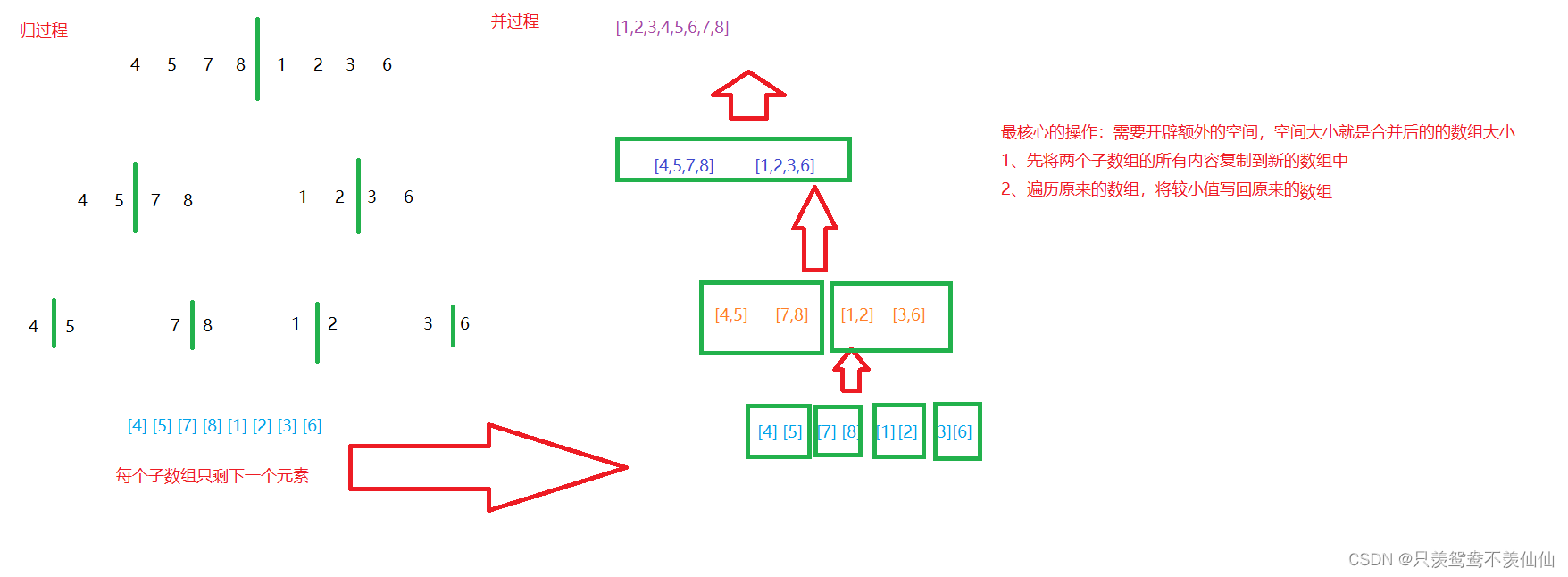
As shown in the figure , Traverse two subarrays , Write the smaller value back to the original array arr in

 /**
     *  Merge sort 
     * @param arr
     */
    public static void mergeSort(int[] arr){
        mergSortInternal(arr,0,arr.length-1);
    }

    /**
     *  stay arr[l..r) Practice merging and sorting 
     * @param arr
     * @param l
     * @param r
     */
    private static void mergSortInternal(int[] arr, int l, int r) {
//        // Optimize 2
//        if (r-l<=15){
//            insertionSort(arr,l,r);
//            return;
//        }
        if (l>=r){
            // At this point, the array is an ordered array 
            return;
        }
        int mid=l+(r-l)/2;
        mergSortInternal(arr,l,mid);
        mergSortInternal(arr,mid+1,r);
        // here arr[l...mid) and [mid+1...r) It's in order , At this point, you only need to merge the two arrays 
        merge(arr,l,mid,r);
//        // Optimize 2
//        if (arr[mid]>arr[mid+1]){
//            // When the two arrays are out of order , To merge 
//            merge(arr,l,mid,r);
//        }
    }

    private static void insertionSort(int[] arr, int l, int r) {
        for (int i = l+1; i <=r; i++) {
            for (int j = i; j >=l+1&&arr[j]<arr[j-1]; j--) {
                swap(arr,j,j-1);
            }
        }

    }

    /**
     *  take arr[l...mid) and [mid+1...r) And is a large ordered array [l...r)
     * @param arr
     * @param l
     * @param mid
     * @param r
     */
    private static void merge(int[] arr, int l, int mid, int r) {
        // First create a new array temp, Copy the value of the subarray to the first array 
        int[] temp=new int[r-l+1];
        for (int i = 0; i <temp.length; i++) {
            //temp The index subscript of is 0...arr.length-1
            //arr The index subscript of is l...r, The poor l An offset of units 
            temp[i]=arr[i+l];
        }
        // Array 1 The starting subscript of 
        int i=l;
        // Array 2 The starting subscript of 
        int j=mid+1;
        for (int k = l; k <=r; k++) {
            if (i>mid){
                // The first array has been traversed 
                arr[k]=temp[j-l];
                j++;
            }else if(j>r){
                // The second array has been traversed 
                arr[k]=temp[i-l];
                i++;
            }else if(temp[i-l]<=temp[j-l]){
                // take temp[i-l] Write back to arr[k]
                arr[k]=temp[i-l];
                i++;
            }else{
                //arr[i-ll]>temp[j-l], Just write back temp[j-l]
                arr[k]=temp[j-l];
                j++;
            }
        }
    }

7、 ... and 、 Sort exercises

1、 The finger of the sword Offer 51. Reverse pairs in arrays

package Seven_sorts.Leetcode;

/**
 *  Reverse pairs in arrays 
 */
public class jianzhiOffer_reversePairs {
    public int reversePairs(int[] nums){
        return reversePairsInternal(nums,0,nums.length-1);
    }

    /**
     *  stay nums[l...r] Merge and sort on , Returns the sorted reverse pair 
     * @param nums
     * @param l
     * @param r
     * @return
     */
    private int reversePairsInternal(int[] nums, int l, int r) {
        // At this time, the array is empty or the array has only one element 
        if (l>=r){
              return 0;
          }
        int mid=l+(r-l)/2;
        // First, find the number of pairs in reverse order of the first sub array 
        int leftCount=reversePairsInternal(nums,l,mid);
        // In finding the number of pairs in reverse order of the second sub array 
        int rightCount=reversePairsInternal(nums,mid+1,r);
        if (nums[mid]>nums[mid+1]){
            // At this time, the left and right arrays are in order , But there is still reverse order between these two arrays , Then find the reverse order pair of the merging process 
            return leftCount+rightCount+merge(nums,l,mid,r);
        }
        //nums[mid]<nums[mid+1], It shows that the whole array is in order at this time , There is no reverse order pair 
        return leftCount+rightCount;
    }

    /**
     *  Merge two ordered group arrays nums[l...mid] and nums[mid+1], Return the number of pairs in reverse order with the merger 
     * @param nums
     * @param l
     * @param mid
     * @param r
     * @return
     */
    private int merge(int[] nums, int l, int mid, int r) {
        // The number of reverse pairs generated after merging 
        int count=0;
        int temp[] =new int[r-l+1];
        for (int i = l; i <=r; i++) {
            temp[i-l]=nums[i];
        }
        int i=l,j=mid+1;
        for (int k = l; k <=r; k++) {
            if (i>mid){
                // The first array has been processed , Directly splice the second array , At this time, there is no reverse order 
                nums[k]=temp[j-l];
                j++;
            } else if (j>r) {
                // The second array has been processed , Directly splice the first array , At this time, there is no reverse order 
                nums[k]=temp[i-l];
                i++;
            } else if (temp[i-l]<=temp[j-l]) {
                nums[k]=temp[i-l];
                i++;
            }else {
                // At this point, the first array element > The second array element , from i Start to mid All elements that end are compared to arr[j] It's all in reverse order 
                // The number of pairs in reverse order is mid-i+1
                count+=mid-i+1;
                nums[k]=temp[j-l];
                j++;
            }
        }
        return count;
    }

}

2、 Sort list

package Seven_sorts.Leetcode;

/**
 *  Sort list 
 */
public class Num148_sortList {
    public ListNode sortList(ListNode head) {
        if (head==null||head.next==null){
            return head;
        }
        // Find the middle node of the list , Split 
        ListNode mid=middle(head);
        ListNode x=head;
        while (x.next!=mid){
            x=x.next;
        }
        x.next=null;
        // First sort the left and right sub linked lists 
        ListNode l1=sortList(head);
        ListNode l2=sortList(mid);
        // Merge two sublink lists 
        return merge(l1,l2);
    }

    /**
     *  Merge two ordered sub linked lists into a large ordered linked list 
     * @param l1
     * @param l2
     * @return
     */
    private ListNode merge(ListNode l1, ListNode l2) {
        if (l1==null){
            return l2;
        }
        if (l2==null){
            return l1;
        }
        if (l1.val<=l2.val) {
            l1.next = merge(l1.next, l2);
            return l1;
        }else {
            l2.next=merge(l1,l2.next);
            return l2;
        }
    }

    /**
     *  Find the middle node of the list 
     * @param head
     * @return
     */
    private ListNode middle(ListNode head) {
        ListNode fir=head;
        ListNode sec=head;
        while (fir!=null&&fir.next!=null){
            fir=fir.next.next;
            sec=sec.next;
        }
        return sec;
    }
    class ListNode {
        int val;
        ListNode next;
        ListNode() {}
        ListNode(int val) { this.val = val; }
        ListNode(int val, ListNode next) { this.val = val; this.next = next; }
    }
}