当前位置:网站首页>leetcode链表专题
leetcode链表专题
2022-07-29 13:05:00 【51CTO】
文章目录
- 数据结构复习(链表)
- 2.环形链表
- 环形链表
- 返回链表中间节点
- 环形链表II
- 环形链表中插入节点,保持环形链表有序
- 3.回文链表
- 回文链表
- 4.相交链表
- 5.删除节点
- 删除链表中的节点
- 删除链表中的指定节点
- 删除排序链表中的重复元素
- 删除排序链表中的重复元素II
- 删除链表的倒数第N个节点
- 从链表中删除总和为0的连续节点
- 6.链表其他题目
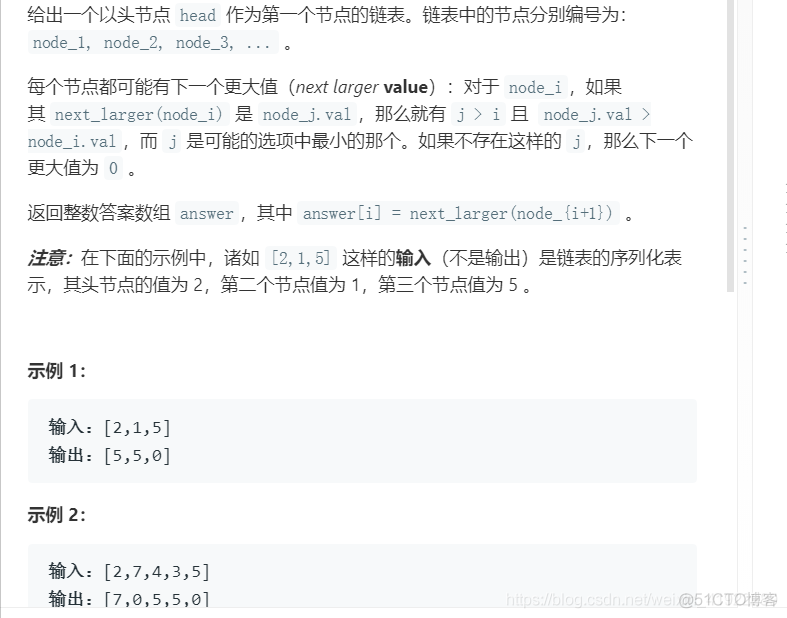
- 链表中的下一个更大的节点
- 两数相加
- 两数相加II
- K个一组反转链表
数据结构复习(链表)
最近在复习算法,为明年的春招做准备,欢迎互关呀,共同学习,进步!
前言
链表是一种常见的基础数据结构,是一种线性表,但是并不会按线性的顺序存储数据,而是在每一个节点里存到下一个节点的指针

由于不必须按顺序存储,链表在插入的时候可以达到 O(1) 的复杂度,比另一种线性表 —— 顺序表快得多,但是查找一个节点或者访问特定编号的节点则需要 O(N)的时间,而顺序表相应的时间复杂度分别是 O(logN) 和 O(1)
使用链表结构可以克服数组链表需要预先知道数据大小的缺点,链表结构可以充分利用计算机内存空间,实现灵活的内存动态管理。但是链表失去了数组随机读取的优点,同时链表由于增加了结点的指针域,空间开销比较大。
基本链表分类:
- 单链表
- 双向链表
- 循环链表
- 跳跃链表
jdk集合中的链表
redis中的链表:
1.反转链表
链表反转I

递归解法
基本思路
其实这里的递归就是相当于遍历到链表最后一个节点,然后从链表尾节点开始反转
使用递归解法,时间复杂度:O(N);空间复杂度:O(N)
基本流程分析

实现:
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode(int x) { val = x; }
* }
*/
class
Solution {
public
ListNode
reverseList(
ListNode
head) {
//空链表或者只有一个节点,则反转结果和原链表一样
if(
head
==
null
||
head.
next
==
null){
return
head;
}
//递归得到的节点是反转后的头结点,所以递归到最后得到的头结点就是反转链表的头结点(原链表最后的节点)
ListNode
newHead
=
reverseList(
head.
next);
//反转逻辑
head.
next.
next
=
head;
//不要忘了尾节点要指向null
head.
next
=
null;
return
newHead;
}
}
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
- 15.
- 16.
- 17.
- 18.
- 19.
- 20.
- 21.
- 22.
- 23.
迭代解法
使用迭代解法的话需要三个指针,前驱指针pre,当前节点指针cur,过渡指针tmp,其实就是从头结点开始,两个节点两个节点的反转,最后讲反转后的尾节点head指向null即可
时间复杂度:O(N);空间复杂度:O(1)
public
ListNode
reverse2(
ListNode
head){
if(
head
==
null){
//空链表
return
null;
}
else
if(
head.
next
==
null){
//单节点链表
return
head;
}
else {
// pre -> cur
ListNode
pre
=
head;
ListNode
cur
=
head.
next;
ListNode
tmp;
//反转逻辑
while (
cur
!=
null) {
// pre -> cur -> cur.next
// tmp = cur.next
tmp
=
cur.
next;
// pre <- cur -> tmp
cur.
next
=
pre;
// pre <- cur -> tmp
// pre -> cur(之后再反转这一部分)
pre
=
cur;
cur
=
tmp;
}
//别忘了反转后的head要指向null
head.
setNext(
null);
return
pre;
}
}
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
- 15.
- 16.
- 17.
- 18.
- 19.
- 20.
- 21.
- 22.
- 23.
- 24.
- 25.
- 26.
- 27.
- 28.
- 29.
反转前N个节点
反转前N个节点和反转链表思路差不多,注意这个

比如这里的可以大概解释下设置tail的目的,递归反转如下:
实现
/**
* 递归反转前N个节点
* 反转以 head 为起点的 n 个节点,返回反转后新的头结点
* @param head
* @return
*/
//后继节点
ListNode
tail
=
null;
public
ListNode
reverseTopNNode(
ListNode
head,
int
n){
if(
n
==
1){
tail
=
head.
next;
return
head;
}
//反转前n - 1个节点
ListNode
newHead
=
reverseTopNNode(
head.
next,
n
-
1);
head.
next.
next
=
head;
//原头结点和tail连接起来
head.
next
=
tail;
return
newHead;
}
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
- 15.
- 16.
- 17.
- 18.
- 19.
- 20.
链表反转II

迭代解法
在迭代解法中,我用到了哑结点的方法
何为哑结点?
哑结点就是一个虚伪的头结点,在原来链表的头结点的前驱增加一个节点指向头结点,方便处理头结点
public
ListNode
reverseBetween(
ListNode
head,
int
m,
int
n) {
if(
m
==
n){
//不用反转
return
head;
}
//设置一个哑结点,处理 m=1 的情况
ListNode
node
=
new
ListNode(
0);
// 0 -> 1 -> 2 -> 3 -> 4 -> 5 -> null
node.
next
=
head;
ListNode
pre
=
node;
ListNode
cur
=
node.
next;
//让cur指向当前 m - 1节点
for(
int
i
=
1;
i
<
m;
i
++){
pre
=
pre.
next;
cur
=
cur.
next;
}
//反转m到n之间的节点,转化为反转前k个节点问题,k = n - m
for(
int
i
=
0;
i
<
n
-
m;
i
++){
//采用头插法,不断地把要反转的节点插到反转区间头节点的前面。重点就是记录第m个结点的前驱结点和第n个结点的后续结点
//现在就是和单链表头插法相似的内容,只是这个插入的节点是从链表中取出,而不是new出来
//头结点:pre
//要插入的节点,当前指针的后继节点(tmp)
ListNode
tmp
=
cur.
next;
//将tmp取出(cur指向tmp的后继),插入到pre和cur之间
cur.
next
=
tmp.
next;
//插入到pre和cur之间
tmp.
next
=
pre.
next;
pre.
next
=
tmp;
}
//真正的头结点是哑结点的next节点
return
node.
next;
}
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
- 15.
- 16.
- 17.
- 18.
- 19.
- 20.
- 21.
- 22.
- 23.
- 24.
- 25.
- 26.
- 27.
- 28.
- 29.
- 30.
- 31.
- 32.
解释下上面头插法和尾插法
在单链表中,节点的插入有两种方法:
- 头插法:每次插入新节点都是在在链表的头结点后插入
- 尾插法:每次插入新节点都是在链表的尾节点后插入
所以,利用插入法实现链表反转(链表逆序)也是一个很好的途径:
原链表:
head
-
>
1
-
>
2
-
>
3
-
>
4
-
>
5
-
>
null
pre
cur
tmp
head
-
>
2
-
>
1
-
>
3
-
>
4
-
>
5
-
>
null
pre
cur
tmp
head
-
>
3
-
>
2
-
>
1
-
>
4
-
>
5
-
>
null
pre
cur
tmp
head
-
>
4
-
>
3
-
>
2
-
>
1
-
>
5
-
>
null
pre
cur
tmp
反转完成
head
-
>
5
-
>
4
-
>
3
-
>
2
-
>
1
-
>
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
- 15.
递归解法
如果使用递归解法的话,可以将其转化为反转链表前n个节点的问题
/**
* 反转指定区间的节点【m,n】
*/
/**
* 递归解法
* @param head
* @param m
* @param n
* @return
*/
public
ListNode
reverseBetween1(
ListNode
head,
int
m,
int
n) {
if(
m
==
1){
//相当于从头结点开始的反转,转化为反转前n个节点的问题
return
reverseN(
head,
n);
}
//其实递归就相当于遍历
head.
next
=
reverseBetween1(
head.
next,
m
-
1,
n
-
1);
return
head;
}
ListNode
tail
=
null;
// 后驱节点
// 反转以 head 为起点的 n 个节点,返回新的头结点
ListNode
reverseN(
ListNode
head,
int
n) {
if (
n
==
1) {
// 记录第 n + 1 个节点
tail
=
head.
next;
return
head;
}
// 以 head.next 为起点,需要反转前 n - 1 个节点
ListNode
last
=
reverseN(
head.
next,
n
-
1);
head.
next.
next
=
head;
// 让反转之后的 head 节点和后面的节点连起来
head.
next
=
tail;
return
last;
}
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
- 15.
- 16.
- 17.
- 18.
- 19.
- 20.
- 21.
- 22.
- 23.
- 24.
- 25.
- 26.
- 27.
- 28.
- 29.
- 30.
- 31.
- 32.
- 33.
- 34.
- 35.
- 36.
基于上面的头插法实现的链表反转:
public
ListNode
reverseList(
ListNode
head) {
if(
head
==
null
||
head.
next
==
null){
return
head;
}
//头插法反转链表
ListNode
pre
=
new
ListNode(
0);
pre.
next
=
head;
ListNode
cur
=
pre.
next;
while(
cur.
next
!=
null){
//要取出来的节点
ListNode
tmp
=
cur.
next;
cur.
next
=
tmp.
next;
tmp.
next
=
pre.
next;
pre.
next
=
tmp;
}
return
pre.
next;
}
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
- 15.
- 16.
- 17.
2.环形链表
环形链表

快慢指针法
快慢双指针,就是快指针的速度是慢指针的两倍
利用这个特点,还可以利用快慢指针解决寻找链表中间节点的问题(快指针走到链表尾节点,由于快指针速度是慢指针的2倍,所以,慢指针会处于链表的中间节点)
而在这里判断有无环,则可以使用快慢指针速度不同的特点,只要快指针和慢指针相遇,此链表必定有环,但是,快慢指针相遇点,不一定是链表环的入口。
时间复杂度:O(N),空间复杂度O(1)
利用哈希表
也可以基于哈希表实现,在遍历链表的过程中,将节点值放入哈希表,只要遇到哈希冲突(相同值),链表就是有环链表
时间复杂度:O(N),空间复杂度:O(N)
返回链表中间节点

刚刚有提到的使用快慢指针返回链表的中间节点
环形链表II

基于哈希表
这个题目要找的是环的入口,那么,基于哈希表的话,只要将发生哈希冲突的节点返回即是答案
时间复杂度:O(N),空间复杂度:O(N)
/**
* 返回链表开始入环的节点
* 【基于哈希表】
* @param head
* @return
*/
public
ListNode
detectCycle(
ListNode
head) {
Set
<
ListNode
>
set
=
new
HashSet
<>();
while(
head
!=
null){
if(
set.
contains(
head)){
return
head;
}
else{
set.
add(
head);
}
head
=
head.
next;
}
return
null;
}
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
- 15.
- 16.
- 17.
- 18.
基于快慢指针
刚刚我也提到过,使用快慢指针虽然能判断一个链表是否有环,但是无法判断快慢指针相遇节点是否是环的入口。
其实在这道题目中,用的是Floyd 算法
何为Floyd 算法?
当然一个跑得快的人和一个跑得慢的人在一个圆形的赛道上赛跑,会发生什么?在某一个时刻,跑得快的人一定会从后面赶上跑得慢的人。
Floyd 的算法被划分成两个不同的 阶段 。在第一阶段,找出列表中是否有环,如果没有环,可以直接返回 null 并退出。否则,用 相遇节点 来找到环的入口。
证明:第二阶段中,从头结点开始遍历,遍历到head = slow时找到环入口

实现:
public
ListNode
detectCycle(
ListNode
head) {
ListNode
slow
=
head;
ListNode
fast
=
head;
boolean
hasCycle
=
false;
//先判断是否有环
while(
fast
!=
null
&&
fast.
next
!=
null){
slow
=
slow.
next;
fast
=
fast.
next.
next;
if(
slow
==
fast){
hasCycle
=
true;
break;
}
}
//如果有环则寻找入环节点
if(
hasCycle){
ListNode
node
=
head;
//从头结点开始寻找,到slow/fast为止,证明过程在上边
while(
node
!=
slow){
slow
=
slow.
next;
node
=
node.
next;
}
return
node;
}
return
null;
}
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
- 15.
- 16.
- 17.
- 18.
- 19.
- 20.
- 21.
- 22.
- 23.
- 24.
- 25.
环形链表中插入节点,保持环形链表有序
这是左神的BAT算法精讲中提到的一道题目,大概意思就是有一个有序的给定头结点环形链表,现在要插入一个指定value的节点到这个环链中,插入完成后保持链表有序
/**
* 环形链表插入节点并且保持链表节点有序
* @param head
* @return
*/
public
ListNode
insertionSortList(
ListNode
head,
int
val) {
//如果链表为空,则生成的node就是头结点,next指针指向自己
if(
head
==
null){
ListNode
node
=
new
ListNode(
val);
node.
next
=
node;
}
//链表不止一个节点
ListNode
node
=
new
ListNode(
val);
ListNode
pre
=
head;
while(
pre.
next
!=
head){
ListNode
cur
=
pre.
next;
if(
cur.
val
>=
node.
val
&&
pre.
val
<=
node.
val){
pre.
next
=
node;
node.
next
=
cur;
}
else{
pre
=
pre.
next;
}
}
//此时,可能出现两种情况,node.val比环形链表中的节点值都小或者都大,此时应该讲node插入到head节点前
pre.
next
=
node;
node.
next
=
head;
return
head;
}
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
- 15.
- 16.
- 17.
- 18.
- 19.
- 20.
- 21.
- 22.
- 23.
- 24.
- 25.
- 26.
- 27.
- 28.
3.回文链表
回文链表

基于快慢指针和链表反转
利用快慢指针找到链表中点,然后反转后半部分链表,再比较前半部分和后半部分是否相同
/**
* 回文链表
*
* @param head
* @return
*/
public
boolean
isPalindrome(
ListNode
head) {
if (
head
==
null
||
head.
next
==
null) {
return
true;
}
ListNode
slow
=
head;
ListNode
fast
=
head;
//快慢指针找到链表中点
while (
fast.
next
!=
null
&&
fast.
next.
next
!=
null) {
fast
=
fast.
next.
next;
slow
=
slow.
next;
}
//反转后半部分
slow
=
reverse(
slow.
next);
//比较前后部分
while (
slow
!=
null) {
if (
slow.
val
!=
head.
val) {
return
false;
}
else {
slow
=
slow.
next;
head
=
head.
next;
}
}
return
true;
}
/**
* 反转链表
*
* @param head
* @return
*/
public
ListNode
reverse(
ListNode
head) {
if (
head
==
null
||
head.
next
==
null) {
return
head;
}
ListNode
newNode
=
reverse(
head.
next);
head.
next.
next
=
head;
head.
next
=
null;
return
newNode;
}
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
- 15.
- 16.
- 17.
- 18.
- 19.
- 20.
- 21.
- 22.
- 23.
- 24.
- 25.
- 26.
- 27.
- 28.
- 29.
- 30.
- 31.
- 32.
- 33.
- 34.
- 35.
- 36.
- 37.
- 38.
- 39.
- 40.
- 41.
- 42.
- 43.
- 44.
- 45.
- 46.
- 47.
基于栈
利用回文链表的顺序和逆序都是相同的特点,遍历链表和遍历出栈比较
public
boolean
isPalindrome(
ListNode
head) {
if (
head
==
null
||
head.
next
==
null) {
return
true;
}
Stack
<
ListNode
>
stack
=
new
Stack();
//将链表所有元素放入栈中,此时出栈节点顺序是链表的逆序
ListNode
p
=
head;
while(
p
!=
null){
stack.
push(
p);
p
=
p.
next;
}
//利用回文链表的顺序和逆序都是相同的特点,遍历链表和遍历出栈比较
ListNode
cur
=
head;
while(
cur
!=
null){
if(
cur.
val
!=
stack.
pop().
val){
return
false;
}
cur
=
cur.
next;
}
return
true;
}
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
- 15.
- 16.
- 17.
- 18.
- 19.
- 20.
- 21.
4.相交链表
找到两个链表相交的起始节点

基于长度计算
计算出两链表长度后,根据长度,从相同起点出发,遍历链表,判断是否相等
public
ListNode
getIntersectionNode(
ListNode
headA,
ListNode
headB) {
if(
headA
==
null
||
headB
==
null) {
return
null;
}
ListNode
a
=
headA;
ListNode
b
=
headB;
int
lenA
=
0;
int
lenB
=
0;
//分别计算长度
while(
a
!=
null){
lenA
++;
a
=
a.
next;
}
while(
b
!=
null){
lenB
++;
b
=
b.
next;
}
//从同一起点出发
while(
lenA
!=
lenB){
if(
lenA
>
lenB){
headA
=
headA.
next;
lenA
--;
}
else{
headB
=
headB.
next;
lenB
--;
}
}
//遍历找到相交点
while(
headA
!=
headB){
headA
=
headA.
next;
headB
=
headB.
next;
}
return
headA;
}
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
- 15.
- 16.
- 17.
- 18.
- 19.
- 20.
- 21.
- 22.
- 23.
- 24.
- 25.
- 26.
- 27.
- 28.
- 29.
- 30.
- 31.
- 32.
- 33.
- 34.
基于哈希表实现
/**
* 基于哈希表
* @param headA
* @param headB
* @return
*/
public
ListNode
getIntersectionNode1(
ListNode
headA,
ListNode
headB) {
if(
headA
==
null
||
headB
==
null) {
return
null;
}
Set
<
ListNode
>
set
=
new
HashSet
<>();
while(
headA
!=
null){
set.
add(
headA);
headA
=
headA.
next;
}
while(
headB
!=
null){
if(
set.
contains(
headB)){
return
headB;
}
else{
headB
=
headB.
next;
}
}
return
null;
}
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
- 15.
- 16.
- 17.
- 18.
- 19.
- 20.
- 21.
- 22.
- 23.
- 24.
返回两个有环链表的相交节点
对于两个有环链表的相交有一下两种情况:
- 第一种情况就是只有一个唯一确定的相交节点
- 第二种情况就是有两个相交节点,返回第一个

5.删除节点
删除链表中的节点

其实这道题目实际上并不是删除了指定节点,而是进行拷贝删除后继节点的操作,意思就是:
- 先拷贝node节点的后继节点值,改变node的val为后继节点val
- 改变node后继指针指向为node后继节点的后继指针指向
这种操作其实是由缺陷的,当要删除的node节点是尾节点,这个操作是行不通的,删除不了尾节点
删除链表中的指定节点

双指针法,在单链表问题中,由于没有像双向链表那样,一个节点具有前驱和后继指针,所以,双指针法在单链表中是一种很好的解决问题的方法,比如下面的删除链表的指定节点,我自定义了两个指针
那么指定了这两个指针后,我们用当前指针遍历链表,只要找到这个指定值
那么双指针操作的简易性就出来了,要删除这个cur指向的节点,只需要前驱指针指向cur指向节点的后继节点,最后更新cur,防止后序还有重复需要删除节点
实现
public
ListNode
removeElements(
ListNode
head,
int
val) {
if(
head
==
null){
return
null;
}
while (
head.
val
==
val) {
head
=
head.
next;
if (
head
==
null) {
return
null;
}
}
//前驱指针
ListNode
pre
=
head;
//当前指针
ListNode
cur
=
head.
next;
while(
cur
!=
null){
if(
cur.
val
==
val){
pre.
next
=
cur.
next;
cur
=
cur.
next;
}
else{
pre
=
pre.
next;
cur
=
cur.
next;
}
}
return
head;
}
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
- 15.
- 16.
- 17.
- 18.
- 19.
- 20.
- 21.
- 22.
- 23.
- 24.
- 25.
删除排序链表中的重复元素

这个题目和上一个题目的区别是,并没有指定要删除的节点,这个节点可以有多种,虽然上题中可以解决重复节点的问题,但是仅限于一种节点
public
ListNode
deleteDuplicate(
ListNode
head) {
if(
head
==
null
||
head.
next
==
null){
return
head;
}
ListNode
cur
=
head;
while(
cur.
next
!=
null){
if(
cur.
val
==
cur.
next.
val){
cur.
next
=
cur.
next.
next;
}
else{
cur
=
cur.
next;
}
}
return
head;
}
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
删除排序链表中的重复元素II

而在这道题目中,与上题不同的是,重复节点要全部删除

实现:
public
ListNode
deleteDuplicates(
ListNode
head) {
if(
head
==
null
||
head.
next
==
null){
return
head;
}
//避免开头就出现重复数字,因此使用哑结点
ListNode
dump
=
new
ListNode(
-
1);
dump.
next
=
head;
ListNode
p
=
dump;
//遍历查找重复节点
while(
p.
next
!=
null
&&
p.
next.
next
!=
null){
//找到一个重复节点,就用val记录
if(
p.
next.
val
==
p.
next.
next.
val){
int
val
=
p.
next.
val;
//循环向后继续再找相同的重复节点
while(
p.
next
!=
null
&&
p.
next.
val
==
val){
//删除重复节点
p.
next
=
p.
next.
next;
}
}
else{
p
=
p.
next;
}
}
return
dump.
next;
}
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
- 15.
- 16.
- 17.
- 18.
- 19.
- 20.
- 21.
- 22.
- 23.
- 24.
删除链表的倒数第N个节点

方法一:
- 反转顺序,倒数第n个就是顺数第sum - n个,然后遍历到遍历到(sum - n)- 1个节点,再删除节点
public
ListNode
removeNthFromEnd(
ListNode
head,
int
n) {
ListNode
dump
=
new
ListNode(
-
1);
dump.
next
=
head;
ListNode
p
=
head;
int
sum
=
0;
while(
p
!=
null){
sum
++;
p
=
p.
next;
}
//反转顺序,倒数第n个就是顺数第sum - n个
sum
-=
n;
p
=
dump;
//遍历到(sum - n)- 1个节点
while(
sum
>
0){
sum
--;
p
=
p.
next;
}
//删除节点
p.
next
=
p.
next.
next;
return
dump.
next;
}
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
- 15.
- 16.
- 17.
- 18.
- 19.
- 20.
- 21.
方法二:
- 一次遍历优化(双指针),第一个指针从列表的开头向前移动 n+1 步,而第二个指针将从列表的开头出发。现在,这两个指针被 n 个结点分开。我们通过同时移动两个指针向前来保持这个恒定的间隔,直到第一个指针到达最后一个结点。此时第二个指针将指向从最后一个结点数起的第 n 个结点。
这样解释吧,假设现在链表节点数是2n个
- 第一个指针先走n+1个节点,还剩下 2n - (n + 1) = n - 1个节点
- 然后第二个指针和第一个指针同时走,直到第一个指针走完链表
- 此时第二个节点离走完链表还差n - 1个节点,即处于倒数第n-1个节点上,倒数第 n 个节点就是其后继
public
ListNode
removeNthFromEnd(
ListNode
head,
int
n) {
ListNode
dump
=
new
ListNode(
-
1);
dump.
next
=
head;
ListNode
p
=
dump;
ListNode
q
=
dump;
//p指针先走n + 1歩
for(
int
i
=
1;
i
<=
n
+
1;
i
++){
p
=
p.
next;
}
//p q同时开始走,知道p走到链表末尾为止
while(
p
!=
null){
p
=
p.
next;
q
=
q.
next;
}
//此时p q之间有n个节点,q处于 倒数n - 1个节点
q.
next
=
q.
next.
next;
return
dump.
next;
}
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
- 15.
- 16.
- 17.
- 18.
从链表中删除总和为0的连续节点

public
ListNode
removeZeroSumSublists(
ListNode
head) {
ListNode
dump
=
new
ListNode(
-
1);
dump.
next
=
head;
ListNode
pre
=
dump;
while(
pre.
next
!=
null){
ListNode
p
=
pre.
next;
ListNode
q
=
p;
//sum是【p,q】区间的节点值和
int
sum
=
p.
val;
while(
q.
next
!=
null
||
sum
==
0){
if(
sum
==
0){
//删除
pre.
next
=
q.
next;
break;
}
q
=
q.
next;
sum
+=
q.
val;
}
if(
sum
!=
0) {
pre
=
pre.
next;
}
}
return
dump.
next;
}
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
- 15.
- 16.
- 17.
- 18.
- 19.
- 20.
- 21.
- 22.
- 23.
- 24.
6.链表其他题目
链表中的下一个更大的节点
public
int[]
nextLargerNodes(
ListNode
head) {
if(
head
==
null
||
head.
next
==
null){
int[]
res
=
new
int[
1];
res[
0]
=
0;
return
res;
}
//链表节点数
int
size
=
0;
//stack1:逆序存储链表,栈顶是链表的最后一个节点
Stack
<
Integer
>
stack1
=
new
Stack
<>();
while(
head
!=
null){
stack1.
push(
head.
val);
head
=
head.
next;
size
++;
}
//stack2:储存当前节点前的节点
Stack
<
Integer
>
stack2
=
new
Stack
<>();
int[]
res
=
new
int[
size];
while(
!
stack1.
isEmpty()){
size
--;
while(
!
stack2.
isEmpty()
&&
stack1.
peek()
>=
stack2.
peek()){
//比当前节点小的节点全都出栈
stack2.
pop();
}
//如果stack2没有节点,栈为空,则没有节点比当前节点大
if(
stack2.
isEmpty()){
res[
size]
=
0;
}
else{
res[
size]
=
stack2.
peek();
}
stack2.
push(
stack1.
pop());
}
return
res;
}
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
- 15.
- 16.
- 17.
- 18.
- 19.
- 20.
- 21.
- 22.
- 23.
- 24.
- 25.
- 26.
- 27.
- 28.
- 29.
- 30.
- 31.
- 32.
- 33.
- 34.
两数相加

/**
* 两数相加
* @param l1
* @param l2
* @return
*/
public
ListNode
addTwoNumbers(
ListNode
l1,
ListNode
l2) {
//哑结点
ListNode
h
=
new
ListNode(
0);
ListNode
cur
=
h;
//进位
int
c
=
0;
while(
l1
!=
null
||
l2
!=
null
||
c
!=
0){
int
l1Val
= (
l1
!=
null
?
l1.
val :
0);
int
l2Val
= (
l2
!=
null
?
l2.
val :
0);
int
tmpSum
=
l1Val
+
l2Val
+
c;
c
=
tmpSum
/
10;
ListNode
tmp
=
new
ListNode(
tmpSum
%
10);
cur.
next
=
tmp;
cur
=
cur.
next;
if(
l1
!=
null) {
l1
=
l1.
next;
}
if(
l2
!=
null) {
l2
=
l2.
next;
}
}
return
h.
next;
}
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
- 15.
- 16.
- 17.
- 18.
- 19.
- 20.
- 21.
- 22.
- 23.
- 24.
- 25.
- 26.
- 27.
- 28.
- 29.
两数相加II

/**
* 两数相加II
* @param l1
* @param l2
* @return
*/
public
ListNode
addTwoNumbers2(
ListNode
l1,
ListNode
l2) {
//栈
LinkedList
<
Integer
>
s1
=
new
LinkedList
<>();
LinkedList
<
Integer
>
s2
=
new
LinkedList
<>();
while(
l1
!=
null) {
s1.
addFirst(
l1.
val);
l1
=
l1.
next;
}
while(
l2
!=
null) {
s2.
addFirst(
l2.
val);
l2
=
l2.
next;
}
int
carry
=
0;
ListNode
lastNode
=
null;
while(
!
s1.
isEmpty()
||
!
s2.
isEmpty()) {
int
a1
=
0,
a2
=
0;
if(
!
s1.
isEmpty()) {
a1
=
s1.
removeFirst();
}
if(
!
s2.
isEmpty()) {
a2
=
s2.
removeFirst();
}
ListNode
curNode
=
new
ListNode((
a1
+
a2
+
carry)
%
10);
carry
= (
a1
+
a2
+
carry)
/
10;
curNode.
next
=
lastNode;
lastNode
=
curNode;
}
if(
carry
>
0) {
ListNode
curNode
=
new
ListNode(
carry);
curNode.
next
=
lastNode;
lastNode
=
curNode;
}
return
lastNode;
}
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
- 15.
- 16.
- 17.
- 18.
- 19.
- 20.
- 21.
- 22.
- 23.
- 24.
- 25.
- 26.
- 27.
- 28.
- 29.
- 30.
- 31.
- 32.
- 33.
- 34.
- 35.
- 36.
- 37.
- 38.
- 39.
- 40.
K个一组反转链表

基于栈实现
/**
* 给你一个链表,每 k 个节点一组进行翻转,请你返回翻转后的链表。
* k 是一个正整数,它的值小于或等于链表的长度。
* 如果节点总数不是 k 的整数倍,那么请将最后剩余的节点保持原有顺序。
*
* 示例 :
* 给定这个链表:1->2->3->4->5
* 当 k = 2 时,应当返回: 2->1->4->3->5
* 当 k = 3 时,应当返回: 3->2->1->4->5
* @param head
* @param k
* @return
*/
public
ListNode
reverseKGroup(
ListNode
head,
int
k) {
ListNode
dumy
=
new
ListNode(
0);
ListNode
p
=
dumy;
Deque
<
ListNode
>
stack
=
new
ArrayDeque
<>();
while(
true){
//记录是否到达k个
int
count
=
0;
//记录每k个的节点逆序前的头结点
ListNode
tmp
=
head;
while(
count
!=
k
&&
tmp
!=
null){
//进栈
stack.
add(
tmp);
tmp
=
tmp.
next;
count
++;
}
//如果最后不足k个,则不需要逆序,直接接起来
if(
count
!=
k){
p.
next
=
head;
break;
}
while(
!
stack.
isEmpty()){
//完成逆序
p.
next
=
stack.
pollLast();
p
=
p.
next;
}
//前k个完成逆序后指向下k个逆序的头结点
p.
next
=
tmp;
head
=
tmp;
}
return
dumy.
next;
}
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
- 15.
- 16.
- 17.
- 18.
- 19.
- 20.
- 21.
- 22.
- 23.
- 24.
- 25.
- 26.
- 27.
- 28.
- 29.
- 30.
- 31.
- 32.
- 33.
- 34.
- 35.
- 36.
- 37.
- 38.
- 39.
- 40.
- 41.
- 42.
- 43.
- 44.
边栏推荐
- IJCAI 2022 outstanding papers published, China won two draft in 298 the first author
- Bika LIMS - SENAITE using open source LIMS set (users, roles and departments)
- HCIP第十三天笔记(BGP的路由过滤、BGP的社团属性、MPLS)
- Hash table implementation code
- Bika LIMS 开源LIMS集—— SENAITE的使用(分析/测试、方法)
- A recent paper summarizes
- 关闭线程池 shutdown 和 shutdownNow 的区别
- Dataset:Medical Data and Hospital Readmissions医疗数据和医院再入院情况数据集的简介、下载、使用方法之详细攻略
- [MySQL view] View concept, create, view, delete and modify
- Go - reading (7), CopySheet Excelize API source code (the from and to the int)
猜你喜欢

【C#】WCF和TCP消息通信练习,实现聊天功能

Gee engine modification UI interface graphic tutorial
Mysql stored procedures, rounding

阿里云官方 Redis 开发规范!

图解 Attention(完整版)!

C language game ------ greedy snake ---- for Xiaobai

How to set the explosion rate of legendary humanoid?Humanoid increase tutorial

Leetcode67. 二进制求和

The IDEA of Database plug-in Database Navigator plug-in

如何成为一名获得 Adobe 国际认证的专业设计师?
随机推荐
IO flow: node flow and process flow summarized in detail.
【LeetCode】Day105-递增的三元子序列
Create and copy conda environment
MySQL八股文背诵版
MySQL 安装报错的解决方法
Leetcode66. 加一
传奇版本添加npc修改增加npc方法以及配置参数教程
25年来最经典的电影特效名场面
The IDEA of Database plug-in Database Navigator plug-in
别再问我如何制作甘特图了!
十种实现延迟任务的方案
Error EPERM operation not permitted, mkdir ‘Dsoftwarenodejsnode_cache_cacach两种解决办法
从零开发一款相机APP, Day03: Camera 常用api和最新框架介绍
MySQL基础篇(三)-- 数据类型
MySQL常用的日期时间函数
Nacos hierarchical storage model - the cluster configuration and NacosRule load balance
Mysql stored procedures, rounding
为什么用了大牌工具后报表开发依然头痛
[Numpy] 创建数组
mariadbackup物理备份使用——筑梦之路