【C语言刷题】Leetcode238——除自身以外数组的乘积

Leetcode238——除自身以外数组的乘积

题目描述

给你一个整数数组 nums，返回数组 answer ，其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。
题目数据保证数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位整数范围内。
请不要使用除法，且在 O(n) 时间复杂度内完成此题。

链接：Leetcode238

示例 1
输入: nums = [1,2,3,4] 输出: [24,12,8,6]
示例 2
输入: nums = [-1,1,0,-3,3] 输出: [0,0,9,0,0]

提示
2 <= nums.length <= 105
-30 <= nums[i] <= 30
保证数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位整数范围内

进阶
你可以在O(1) 的额外空间复杂度内完成这个题目吗？（ 出于对空间复杂度分析的目的，输出数组不被视为额外空间。）

核心代码模式

/** * Note: The returned array must be malloced, assume caller calls free(). */
//第一个参数是目标数组的指针，第二个参数是目标数组大小，第三个数组是返回数组的大小
//返回值是要返回的数组的指针
int* productExceptSelf(int* nums, int numsSize, int* returnSize)
{
    
    
}

思路分析（C语言）

估计大部分人看到这道题第一时间想到的是把数组所有元素累乘，然后除以某个数就得到其他元素的乘积了，但是题目明确说明了不可以使用除法。
这里就介绍一种容易理解的解法——左右乘积列表

空间复杂度为O(n)的解法

首先，我们把数组中某个元素x前面的元素称为前缀，后面的元素称为后缀，我们要求的是除x外其他元素的乘积，也就相当于求出前缀元素乘积与后缀元素乘积的乘积，这就将问题分解了。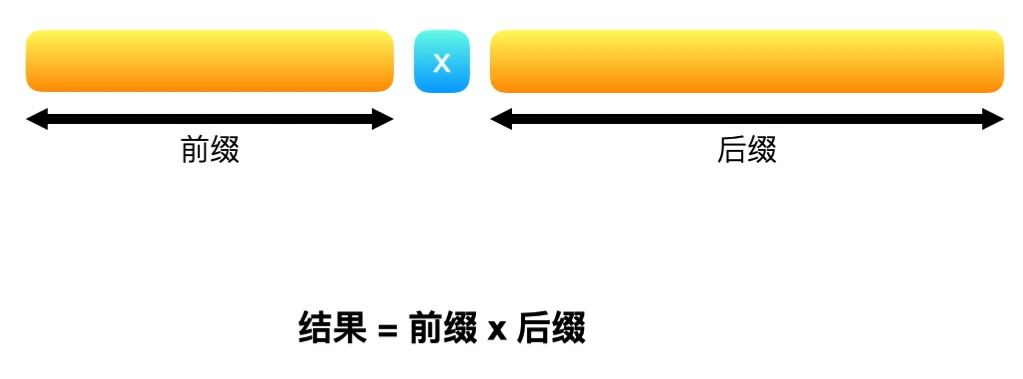

第一个元素是不是没有前缀可言？那它的前缀乘积是多少呢？我们设为1，这样就不会影响计算结果了，因为除第一个元素以外其他元素的乘积就是后缀乘积。同理，最后一个元素的后缀乘积也设为1。
我们创建两个数组L和R分别用来存放前缀乘积和后缀乘积。其中L[0] = 1且R[0] = 1（上面讲的）。
对于数组L，有L[i] = L[i - 1] * nums[i - 1]。如图：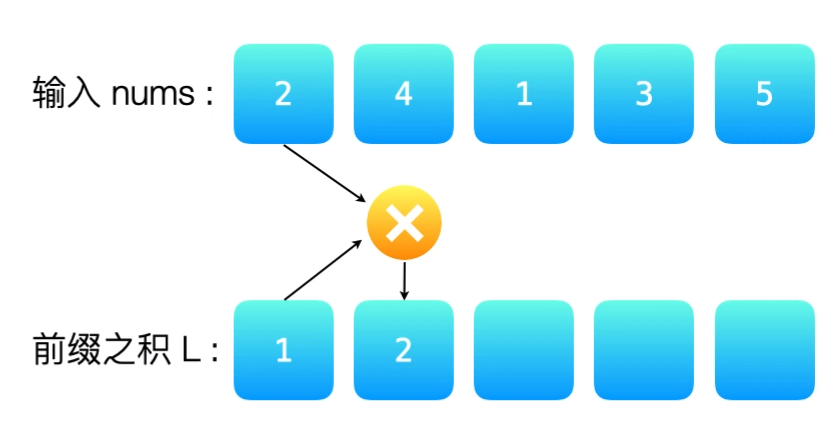


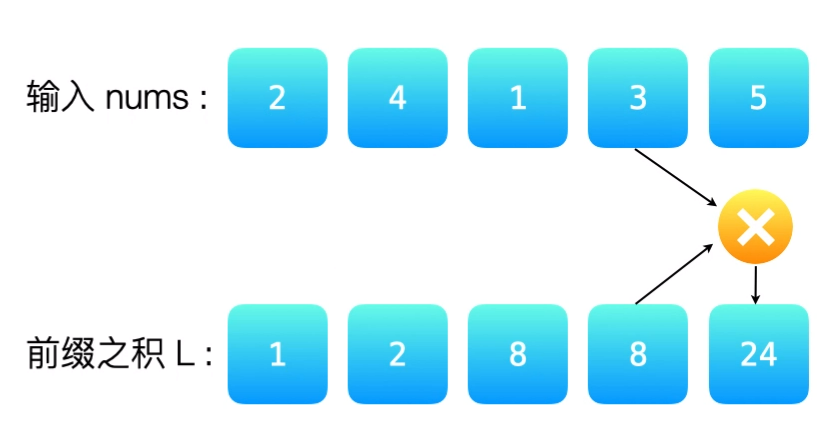
对于数组R，有R[i] = R[i + 1] * nums[i + 1]。如图：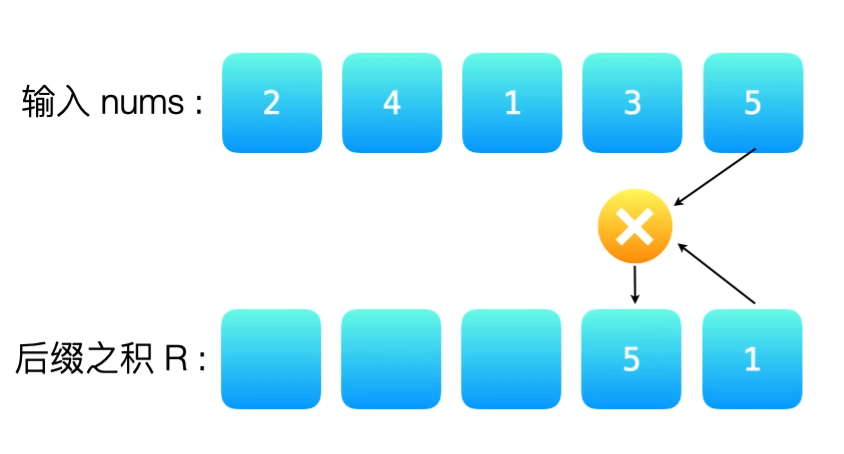


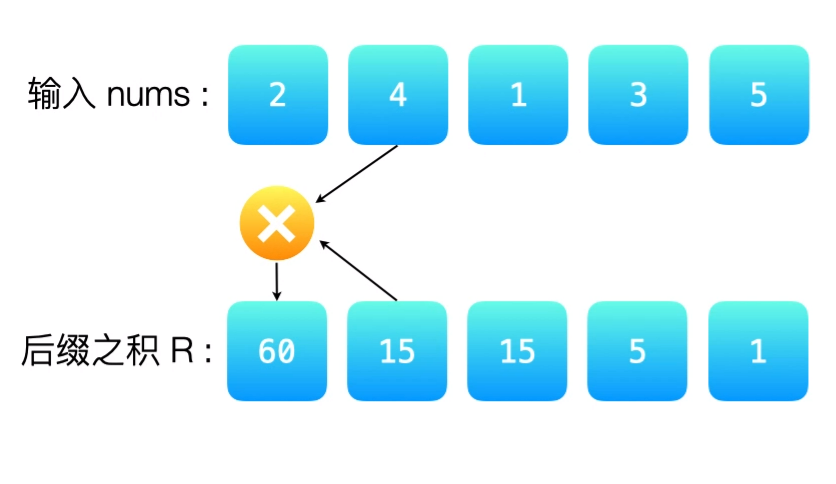
最后再把前缀乘积和后缀乘积一一对应乘起来放到要返回的数组中。

代码实现

int* productExceptSelf(int* nums, int numsSize, int* returnSize)
{
    
    int i = 0;
    int* ans = (int*)malloc(numsSize * sizeof(int));
    int L[numsSize];
    int R[numsSize];
    //两个元素置为1
    L[0] = 1;
    R[numsSize - 1] = 1;
    //计算前缀乘积
    for(i = 1; i < numsSize; i++)
    {
    
        L[i] = L[i - 1] * nums[i - 1];
    }
    //计算后缀乘积
    for(i = numsSize - 2; i >= 0; i--)
    {
    
        R[i] = R[i + 1] * nums[i + 1];
    }
    //前缀后缀乘积再相乘
    for(i = 0; i < numsSize; i++)
        ans[i] = L[i] * R[i];

    *returnSize = numsSize;
    return ans;
}

复杂度分析

空间复杂度为O(1)的解法

还能不能优化呢？
你想啊，可不可以减少创建的数组数量呢？
我们先求的前缀乘积，最后不还是要乘到ans数组里面去嘛，那可不可以直接就把前缀乘积放在ans数组里？那后缀乘积可不可以也不放在另外的数组，而是计算后也直接乘上ans数组的值呢？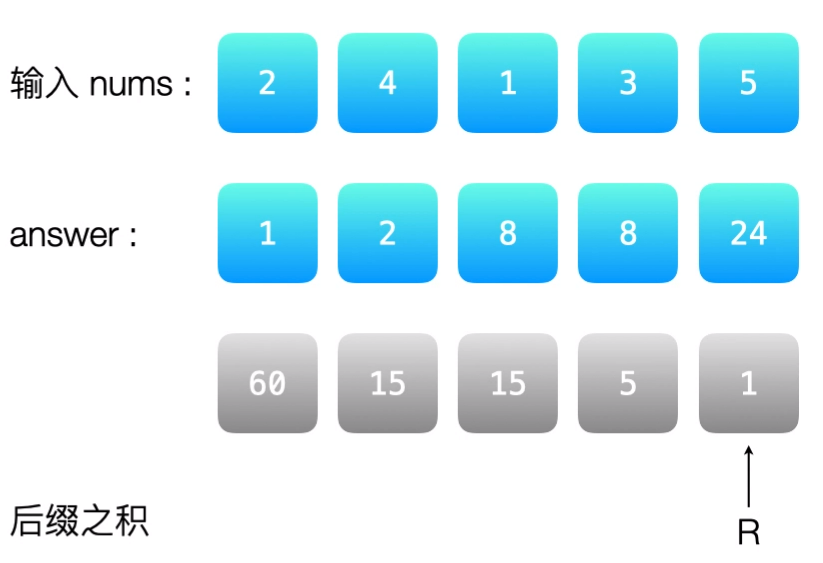

代码实现

int* productExceptSelf(int* nums, int numsSize, int* returnSize)
{
    
    int i = 0;
    int R = 1;
    int* ans = (int*)malloc(numsSize * sizeof(int));

    ans[0] = 1;
    ans[numsSize - 1] = 1;
    //前缀乘积
    for (i = 1; i < numsSize; i++)
    {
    
        ans[i] = ans[i - 1] * nums[i - 1];
    }
    //后缀乘积
    for (i = numsSize - 1; i >= 0; i--)
    {
       
        ans[i] *= R;
        R *= nums[i];
    }

    *returnSize = numsSize;
    return ans;
}

复杂度分析