当前位置:网站首页>Leetcode(695)——岛屿的最大面积
Leetcode(695)——岛屿的最大面积
2022-07-05 20:09:00 【SmileGuy17】
Leetcode(695)——岛屿的最大面积
题目
给你一个大小为 m × n m \times n m×n 的二进制矩阵 grid 。
岛屿 是由一些相邻的 1 (代表土地) 构成的组合,这里的「相邻」要求两个 1 必须在 水平或者竖直的四个方向上 相邻。你可以假设 grid 的四个边缘都被 0(代表水)包围着。
岛屿的面积是岛上值为 1 的单元格的数目。
计算并返回 grid 中最大的岛屿面积。如果没有岛屿,则返回面积为 0 。
示例 1:
输入:grid = [[0,0,1,0,0,0,0,1,0,0,0,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,1,1,0,1,0,0,0,0,0,0,0,0],[0,1,0,0,1,1,0,0,1,0,1,0,0],[0,1,0,0,1,1,0,0,1,1,1,0,0],[0,0,0,0,0,0,0,0,0,0,1,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,0,0,0,0,0,0,1,1,0,0,0,0]]
输出:6
解释:答案不应该是 11 ,因为岛屿只能包含水平或垂直这四个方向上的 1 。
示例 2:
输入:grid = [[0,0,0,0,0,0,0,0]]
输出:0
提示:
- m == grid.length
- n == grid[i].length
- 1 1 1 <= m, n <= 50 50 50
- grid[i][j] 为 0 0 0 或 1 1 1
题解
方法一:DFS(递归写法)
思路
- 我们想知道网格中每个连通形状的面积,然后取最大值。
- 如果我们在一个土地上,以 4 4 4 个方向探索与之相连的每一个土地(以及与这些土地相连的土地),那么探索过的土地总数将是该连通形状的面积。
- 为了确保每个土地访问不超过一次,我们每次经过一块土地时,将这块土地的值置为 0 0 0。这样我们就不会多次访问同一土地。
这里我们使用了一个小技巧,对于四个方向的遍历,可以创造一个数组 [-1, 0, 1, 0, -1],每相邻两位即为上下左右四个方向之一。
在辅函数里,一个一定要注意的点是辅函数内递归搜索时,边界条件的判定。边界判定一般有两种写法,一种是先判定是否越界,只有在合法的情况下才进行下一步搜索(即判断放在调用递归函数前);另一种是不管三七二十一先进行下一步搜索,待下一步搜索开始时再判断是否合法(即判断放在辅函数第一行)。我们这里分别展示这两种写法。
代码实现
Leetcode 官方题解:
class Solution {
int dfs(vector<vector<int>>& grid, int cur_i, int cur_j) {
if (cur_i < 0 || cur_j < 0 || cur_i == grid.size() || cur_j == grid[0].size() || grid[cur_i][cur_j] != 1) {
return 0;
}
grid[cur_i][cur_j] = 0;
int di[4] = {
0, 0, 1, -1};
int dj[4] = {
1, -1, 0, 0};
int ans = 1;
for (int index = 0; index != 4; ++index) {
int next_i = cur_i + di[index], next_j = cur_j + dj[index];
ans += dfs(grid, next_i, next_j);
}
return ans;
}
public:
int maxAreaOfIsland(vector<vector<int>>& grid) {
int ans = 0;
for (int i = 0; i != grid.size(); ++i) {
for (int j = 0; j != grid[0].size(); ++j) {
ans = max(ans, dfs(grid, i, j));
}
}
return ans;
}
};
我自己的:
class Solution {
void DFS(vector<vector<int>>& grid, int x, int y, int& area){
if(0 > x || x >= grid[0].size() || y >= grid.size() || 0 > y) return;
if(grid[y][x] == 1){
// 上下左右
area += 1;
grid[y][x] = 0; // 置为0防止再次访问该点
DFS(grid, x-1, y, area);
DFS(grid, x+1, y, area);
DFS(grid, x, y-1, area);
DFS(grid, x, y+1, area);
}
}
public:
int maxAreaOfIsland(vector<vector<int>>& grid) {
int ans = 0, area, yn = grid.size(), xn = grid[0].size();
for(int y = 0; y < yn; y++){
for(int x = 0; x < xn; x++){
if(grid[y][x] == 1){
area = 0;
DFS(grid, x, y, area);
ans = ans < area? area: ans;
}
}
}
return ans;
}
};
复杂度分析
时间复杂度: O ( m × n ) O(m×n) O(m×n)。其中 m m m 是给定网格中的行数, n n n 是列数。我们访问每个原本为1的网格最多一次。
空间复杂度: O ( m × n ) O(m \times n) O(m×n),递归的深度最大可能是整个网格的大小,因此最大可能使用 O ( m × n ) O(m \times n) O(m×n) 的栈空间。
方法二:DFS + 辅助栈(迭代写法)
思路
原理与方法一相同,只是实现方式采用了迭代而不是递归,并使用栈辅助实现。
- 方法一通过函数的调用来表示接下来想要遍历哪些土地,让下一层函数来访问这些土地。而方法二把接下来想要遍历的土地放在栈里,然后在取出这些土地的时候访问它们。
- 访问每一片土地时,我们将对围绕它四个方向进行探索,找到还未访问的土地,加入到栈 stack \textit{stack} stack 中;
- 另外,只要栈 stack \textit{stack} stack 不为空,就说明我们还有土地待访问,那么就从栈中取出一个元素并访问。
代码实现
Leetcode 官方题解:
class Solution {
public:
int maxAreaOfIsland(vector<vector<int>>& grid) {
int ans = 0;
for (int i = 0; i != grid.size(); ++i) {
for (int j = 0; j != grid[0].size(); ++j) {
int cur = 0;
stack<int> stacki;
stack<int> stackj;
stacki.push(i);
stackj.push(j);
while (!stacki.empty()) {
int cur_i = stacki.top(), cur_j = stackj.top();
stacki.pop();
stackj.pop();
if (cur_i < 0 || cur_j < 0 || cur_i == grid.size() || cur_j == grid[0].size() || grid[cur_i][cur_j] != 1) {
continue;
}
++cur;
grid[cur_i][cur_j] = 0;
int di[4] = {
0, 0, 1, -1};
int dj[4] = {
1, -1, 0, 0};
for (int index = 0; index != 4; ++index) {
int next_i = cur_i + di[index], next_j = cur_j + dj[index];
stacki.push(next_i);
stackj.push(next_j);
}
}
ans = max(ans, cur);
}
}
return ans;
}
};
我自己的:
class Solution {
public:
int maxAreaOfIsland(vector<vector<int>>& grid) {
int ans = 0, area, yn = grid.size(), xn = grid[0].size();
stack<pair<int, int>> island;
pair<int, int> tmp;
for(int y = 0; y < yn; y++){
for(int x = 0; x < xn; x++){
if(grid[y][x] == 1){
area = 0;
island.push(make_pair(y, x));
while(!island.empty()){
tmp.first = island.top().first;
tmp.second = island.top().second;
island.pop();
if(grid[tmp.first][tmp.second] != 1) continue;
grid[tmp.first][tmp.second] = 0;
area++;
if(tmp.second-1 >= 0) island.push(make_pair(tmp.first, tmp.second-1));
if(tmp.second+1 < xn) island.push(make_pair(tmp.first, tmp.second+1));
if(tmp.first-1 >= 0) island.push(make_pair(tmp.first-1, tmp.second));
if(tmp.first+1 < yn) island.push(make_pair(tmp.first+1, tmp.second));
}
ans = max(area, ans);
}
}
}
return ans;
}
};
复杂度分析
时间复杂度: O ( m × n ) O(m \times n) O(m×n)。其中 m m m 是给定网格中的行数, n n n 是列数。我们访问每个原本为1的网格最多一次。
空间复杂度: O ( m × n ) O(m \times n) O(m×n),栈中最多会存放所有的土地,土地的数量最多为 m × n m \times n m×n 块,因此使用的空间为 O ( m × n ) O(m \times n) O(m×n)。
方法三:BFS + 队列
思路
把方法二中的栈改为队列,每次从队首取出土地,并将接下来想要遍历的土地放在队尾,就实现了广度优先搜索算法。
代码实现
Leetcode 官方题解:
class Solution {
public:
int maxAreaOfIsland(vector<vector<int>>& grid) {
int ans = 0;
for (int i = 0; i != grid.size(); ++i) {
for (int j = 0; j != grid[0].size(); ++j) {
int cur = 0;
queue<int> queuei;
queue<int> queuej;
queuei.push(i);
queuej.push(j);
while (!queuei.empty()) {
int cur_i = queuei.front(), cur_j = queuej.front();
queuei.pop();
queuej.pop();
if (cur_i < 0 || cur_j < 0 || cur_i == grid.size() || cur_j == grid[0].size() || grid[cur_i][cur_j] != 1)
continue;
++cur;
grid[cur_i][cur_j] = 0;
int di[4] = {
0, 0, 1, -1};
int dj[4] = {
1, -1, 0, 0};
for (int index = 0; index != 4; ++index) {
int next_i = cur_i + di[index], next_j = cur_j + dj[index];
queuei.push(next_i);
queuej.push(next_j);
}
}
ans = max(ans, cur);
}
}
return ans;
}
};
我自己的:
class Solution {
public:
int maxAreaOfIsland(vector<vector<int>>& grid) {
int ans = 0, area, yn = grid.size(), xn = grid[0].size();
queue<pair<int, int>> island;
pair<int, int> tmp;
for(int y = 0; y < yn; y++){
for(int x = 0; x < xn; x++){
if(grid[y][x] == 1){
area = 0;
island.push(make_pair(y, x));
while(!island.empty()){
tmp.first = island.front().first;
tmp.second = island.front().second;
island.pop();
if(grid[tmp.first][tmp.second] != 1) continue;
grid[tmp.first][tmp.second] = 0;
area++;
if(tmp.second-1 >= 0) island.push(make_pair(tmp.first, tmp.second-1));
if(tmp.second+1 < xn) island.push(make_pair(tmp.first, tmp.second+1));
if(tmp.first-1 >= 0) island.push(make_pair(tmp.first-1, tmp.second));
if(tmp.first+1 < yn) island.push(make_pair(tmp.first+1, tmp.second));
}
ans = max(area, ans);
}
}
}
return ans;
}
};
复杂度分析
时间复杂度: O ( m × n ) O(m×n) O(m×n)。其中 m m m 是给定网格中的行数, n n n 是列数。我们访问每个原本为1的网格最多一次。
空间复杂度: O ( m × n ) O(m \times n) O(m×n),队列中最多会存放所有的土地,土地的数量最多为 m × n m \times n m×n 块,因此使用的空间为 O ( m × n ) O(m \times n) O(m×n)。
边栏推荐
- Leetcode skimming: binary tree 16 (path sum)
- B站UP搭建世界首个纯红石神经网络、基于深度学习动作识别的色情检测、陈天奇《机器学编译MLC》课程进展、AI前沿论文 | ShowMeAI资讯日报 #07.05
- Fundamentals of deep learning convolutional neural network (CNN)
- selenium 元素信息
- c——顺序结构
- 2023年深圳市绿色低碳产业扶持计划申报指南
- 多分支结构
- CADD课程学习(7)-- 模拟靶点和小分子相互作用 (半柔性对接 AutoDock)
- 线程池参数及合理设置
- 【数字IC验证快速入门】8、数字IC中的典型电路及其对应的Verilog描述方法
猜你喜欢
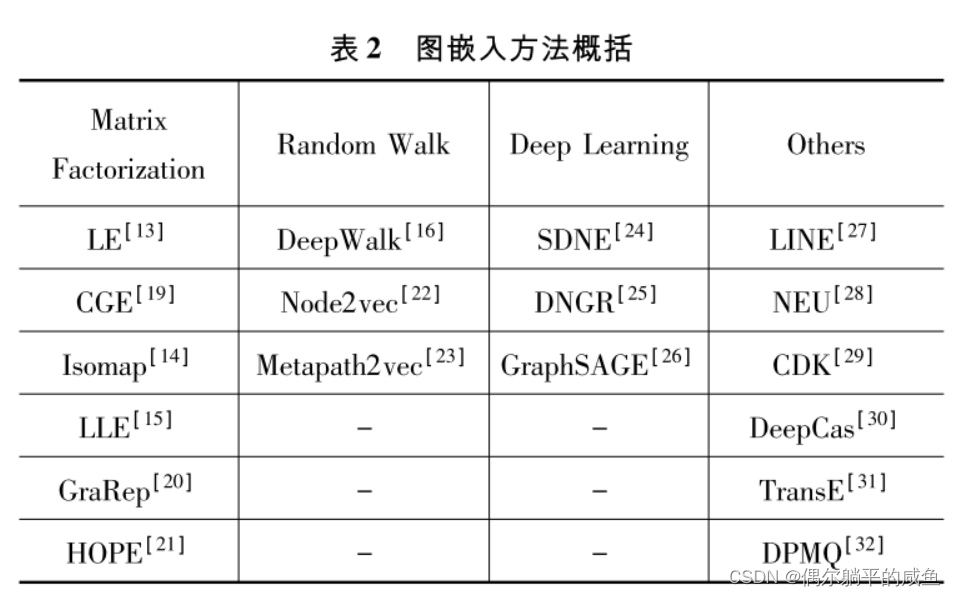
图嵌入Graph embedding学习笔记

Parler de threadlocal insecurerandom

Leetcode skimming: binary tree 12 (all paths of binary tree)

No matter how busy you are, you can't forget safety

leetcode刷题:二叉树15(找树左下角的值)
Scala基础【HelloWorld代码解析,变量和标识符】

kubernetes资源对象介绍及常用命令(五)-(ConfigMap&Secret)
Wechat applet regular expression extraction link
Leetcode skimming: binary tree 10 (number of nodes of a complete binary tree)

leetcode刷题:二叉树14(左叶子之和)
随机推荐
Tasks in GStreamer
How to safely and quickly migrate from CentOS to openeuler
Fundamentals of deep learning convolutional neural network (CNN)
ByteDance dev better technology salon was successfully held, and we joined hands with Huatai to share our experience in improving the efficiency of web research and development
Guidelines for application of Shenzhen green and low carbon industry support plan in 2023
Debezium series: parsing the default value character set
c语言oj得pe,ACM入门之OJ~
【c语言】快速排序的三种实现以及优化细节
安信证券在网上开户安全吗?
解决Thinkphp框架应用目录下数据库配置信息修改后依然按默认方式连接
Autumn byte interviewer asked you any questions? In fact, you have stepped on thunder
【数字IC验证快速入门】1、浅谈数字IC验证,了解专栏内容,明确学习目标
无卷积骨干网络:金字塔Transformer,提升目标检测/分割等任务精度(附源代码)...
Is it safe to open a mobile stock account? Is it reliable?
. Net distributed transaction and landing solution
Relationship between floating elements and parent and brother boxes
【数字IC验证快速入门】8、数字IC中的典型电路及其对应的Verilog描述方法
【c语言】归并排序
MySql的root密码忘记该怎么找回
字节跳动Dev Better技术沙龙成功举办,携手华泰分享Web研发效能提升经验
