Dynamic programming knapsack problem 01 knapsack explanation

One 、 Problem introduction

1. What is dynamic programming ?

Dynamic programming （ English ：Dynamic programming, abbreviation DP）, It's kind of in math 、 management science 、 Computer science 、 Used in economics and bioinformatics , A method of solving complex problems by decomposing the original problem into relatively simple subproblems . Dynamic programming is often applied to problems with overlapping subproblems and optimal substructure properties
The core idea : By dividing the problem into small problems , Record past results , Reduce repetition
Small example ：

A ： "1+1+1+1+1+1+1+1 =？"
A ： " What is the value of the above equation "
B ：  Calculation  "8"
A :  Write... On the left side of the equation above  "1+"  Well ？
A : " What is the value of the equation "
B :  It's a quick answer  "9"
A : " How can you know the answer so quickly "
A : " As long as 8 On the basis of 1 That's it "
A : " So you don't have to recalculate , Because you remember that the value of the first equation is 8! Dynamic programming algorithm can also be said to be  ' Remember to save time by asking for solutions '"

2. What is the knapsack problem ？

knapsack problem (Knapsack problem) It's a kind of combinatorial optimization NP Problem completely . The problem can be described as ： Given a set of items , Each item has its own weight and price , Within the total weight limit , How do we choose , To maximize the total price of the item . The name of the problem comes from how to choose the most suitable item to put in a given backpack . Similar problems often arise in business 、 Combinatorial mathematics , Computational complexity theory 、 In the fields of cryptography and applied mathematics . The knapsack problem can also be described as a decisive problem , That is, the total weight does not exceed W Under the premise of , Whether the total value can reach V？ It's in 1978 Year by year Merkle and Hellman Proposed .
Common categories ：

1. 01 knapsack
2. Completely backpack
3. Multiple backpack
4. Pack in groups

3. What is? 01 knapsack ？

01 Knapsack is the simplest problem in knapsack problem .01 The constraint of knapsack is to give several items , Each item has and only one , And there are two attributes: weight and volume . stay 01 In the knapsack problem , Because there is only one of each kind , For each item, you only need to consider the selection and non selection . If you don't choose to put it in your backpack , There is no need to deal with . If you choose to put it in your backpack , Because I don't know how much space the previously placed items occupy , You need to enumerate all the situations that may occupy the backpack space after putting this item into the backpack .

4. How to solve the knapsack problem ？

It can be roughly divided into these steps ：

1. State means / Determine the state variable （ function ）
2. State calculation / Set partitioning / Determine the state transfer equation （ Recurrence equation ）
3. Determine the boundary conditions

Two 、 Example explanation

1. subject ：

2. analysis

2.1 First step ： State means

The greatest value is Quantity of articles i and Backpack Capacity j Function of .
Let's set the function f[i][j] Express front i Item Put in Capacity of j The backpack Maximum value of .
The ultimate maximum value is the number of items i from 0 Growth to n, Backpack Capacity j from 0 Growth to m At the time of the f[n][m] value .

2.2 The second step : Determine the state transfer equation

State variables ：f[i][j] Before presentation i The capacity of items is j The biggest value of our backpack

The current capacity is j, We have to consider the second i Item Can you put in ？ Whether to put in ？

1. If the current Backpack Capacity j<v[i], Can't put , be f[i][j]=f[i-1][j]
2. If the current Backpack Capacity j>=v[i], It can be put in, but the cost should be compared
   2.1 If the first i Items are not put into the backpack , be f[i][j]=f[i-1][j]
   2.2 If the first i Put this item into your backpack , be f[i][j]=f[i-1][j-v[i]]+w[i]

If the first i Put this item into your backpack , Then the backpack capacity is left j-v[i], So take the front i-1 Items are put into the remaining capacity of the backpack j-v[i] The maximum value obtained f[i-1][j-v[i]].

State transition equation ：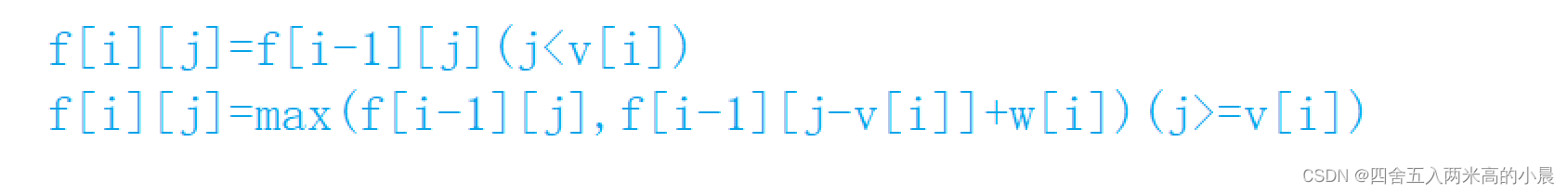

It can be illustrated as :

2.3 The boundary conditions

about 01 For backpacks, the boundary is f[i][j]=0, When i=0 perhaps j=0 when f[i][j] The value of is 0.

i=0 when , It means that there is no item in the backpack , At this time, the maximum value of backpacks is impossible , So for 0;
j=0 when , Indicates that the capacity of the backpack is 0, Then you can't put items at this time , So the maximum value is 0;

3. The process represents

3.1 Core code

3.2 Manual calculation

The green line indicates that every time you put i About items , And it shows its source

3.3 Code validation

3.4 Complete code

#include<iostream>
#include<algorithm>
using namespace std;
const int N=1010;
int n,m;
int v[N],w[N];//v Array storage volume ,w Array storage value 
int f[N][N];
int main ()
{
    
    cin>>n>>m;
    for(int i=1;i<=n;i++) cin>>v[i]>>w[i];
    
    for(int i=1;i<=n;i++)
        for(int j=0;j<=m;j++)
            {
    
                f[i][j]=f[i-1][j];// Will not be placed in the i The condition of an item is combined with the condition that it can be put but not put 
                if(j>=v[i]) f[i][j]=max(f[i][j],f[i-1][j-v[i]]+w[i]);
            }
    cout<<f[n][m]<<endl;
    return 0;
}

3、 ... and 、 Optimize

1. Optimization purpose ：

Optimize the two-dimensional representation into one-dimensional , Reduce the use of space , Use a one-dimensional array f[j] Only one line of data is recorded , Give Way j Value sequence loop , Sequential update f[j]

2. Optimized code < Not necessarily right >

3. Program validation

The answer is clearly wrong , Why? ？？？

4. Error point analysis

If j Is a sequential update , that f[j-v[i]] Will precede f[j] to update , When comparing , In fact, it is comparing with the updated value , This leads to the wrong answer , So here's the solution j Reverse cycle . When j When it is in reverse order ,f[j] Will precede f[j-v[i]] to update , That is to say, use the old value f[j-v[i]] To update f[j], Equivalent to using the previous line f[j-v[i]] Go to more f[j], So the answer is correct .

5. Improved code

There is another small mistake at this time , That's it j The scope is not >=1, because j If it is less than v[i] Will lead to f[j-v[i]] The subscript in becomes negative , So make improvements , The final code is ：