当前位置:网站首页>20220621 Three Conjugates of Dual Quaternions
20220621 Three Conjugates of Dual Quaternions
2022-06-23 05:28:00 【我起个什么名字呢】
Dual Quaternions. Yan-Bin Jia

If we view a dual quaternion σ = p + ϵ q \sigma=p+\epsilon q σ=p+ϵq as just an 8-tuple, its conjugate could be a vector generated from σ \sigma σ by flipping the signs of some of its elements. The dual quaternion indeed has three conjugates, the first of which is from the conjugate of a dual number:
σ ∙ = p − ϵ q . \sigma^{\bullet}=p-\epsilon q . σ∙=p−ϵq.Or, viewed as an 8-tuple, it is
σ ∙ = ( p 0 , p 1 , p 2 , p 3 , − q 0 , − q 1 , − q 2 , − q 3 ) \sigma^{\bullet}=\left(p_{0}, p_{1}, p_{2}, p_{3},-q_{0},-q_{1},-q_{2},-q_{3}\right) σ∙=(p0,p1,p2,p3,−q0,−q1,−q2,−q3)In this sense, the product of σ \sigma σ with σ ∙ \sigma^{\bullet} σ∙ ought to be treated as an inner product to yield a scalar. This is not the case, however, if under the multiplication rule (14), for we have
σ ⊗ σ ∙ = ( p + ϵ q ) ( p − ϵ q ) = p p + ϵ ( q p − p q ) \begin{aligned} \sigma \otimes \sigma^{\bullet} &=(p+\epsilon q)(p-\epsilon q) \\ &=p p+\epsilon(q p-p q) \end{aligned} σ⊗σ∙=(p+ϵq)(p−ϵq)=pp+ϵ(qp−pq)Generally, the quaternion product p p p p pp is not a scalar, and q p ≠ p q q p \neq p q qp=pq following the non-commutativity of quaternion multiplication. The first conjugate is seldom used other than for deriving the third conjugate to be introduced shortly.
The second conjugate of σ \sigma σ follows from the classical quaternion conjugation:
σ ∗ = p ∗ + ϵ q ∗ \sigma^{*}=p^{*}+\epsilon q^{*} σ∗=p∗+ϵq∗
where p ∗ p^{*} p∗ and q ∗ q^{*} q∗ are the conjugates of the quaternions p p p and q q q, respectively. The conjugate σ ∗ \sigma^{*} σ∗ can also be viewed as an 8-tuple:
σ ∗ = ( p 0 , − p 1 , − p 2 , − p 3 , q 0 , − q 1 , − q 2 , − q 3 ) . \sigma^{*}=\left(p_{0},-p_{1},-p_{2},-p_{3}, q_{0},-q_{1},-q_{2},-q_{3}\right) . σ∗=(p0,−p1,−p2,−p3,q0,−q1,−q2,−q3).
Let us calculate the product of σ \sigma σ with σ ∗ \sigma^{*} σ∗ below:
σ ⊗ σ ∗ = ( p + ϵ q ) ( p ∗ + ϵ q ∗ ) = p p ∗ + ϵ ( p q ∗ + q p ∗ ) = ( p 0 2 + p 1 2 + p 2 2 + p 3 2 ) + 2 ϵ ( p 0 q 0 + p 1 q 1 + p 2 q 2 + p 3 q 3 ) = ∥ p ∥ 2 + 2 ϵ ( p 0 q 0 + p ⋅ q ) \begin{aligned} \sigma \otimes \sigma^{*} &=(p+\epsilon q)\left(p^{*}+\epsilon q^{*}\right) \\ &=p p^{*}+\epsilon\left(p q^{*}+q p^{*}\right) \\ &=\left(p_{0}^{2}+p_{1}^{2}+p_{2}^{2}+p_{3}^{2}\right)+2 \epsilon\left(p_{0} q_{0}+p_{1} q_{1}+p_{2} q_{2}+p_{3} q_{3}\right) \\ &=\|p\|^{2}+2 \epsilon\left(p_{0} q_{0}+\boldsymbol{p} \cdot \boldsymbol{q}\right) \end{aligned} σ⊗σ∗=(p+ϵq)(p∗+ϵq∗)=pp∗+ϵ(pq∗+qp∗)=(p02+p12+p22+p32)+2ϵ(p0q0+p1q1+p2q2+p3q3)=∥p∥2+2ϵ(p0q0+p⋅q)
It is a dual scalar but not a scalar unless p 0 q 0 + p ⋅ q = 0 p_{0} q_{0}+\boldsymbol{p} \cdot \boldsymbol{q}=0 p0q0+p⋅q=0, that is, unless p p p and q q q are orthogonal 4-tuples.
The third conjugate of σ \sigma σ combines the first two conjugation operators:
σ ⋄ = p ∗ − ϵ q ∗ \sigma^{\diamond}=p^{*}-\epsilon q^{*} σ⋄=p∗−ϵq∗
As an 8-tuple, it takes the form
σ ∘ = ( p 0 , − p 1 , − p 2 , − p 3 , − q 0 , q 1 , q 2 , q 3 ) . \sigma^{\circ}=\left(p_{0},-p_{1},-p_{2},-p_{3},-q_{0}, q_{1}, q_{2}, q_{3}\right) . σ∘=(p0,−p1,−p2,−p3,−q0,q1,q2,q3).
Similarly, we calculate the product of σ \sigma σ with the above conjugate:
σ ⊗ σ ⋄ = ( p + ϵ q ) ( p ∗ − ϵ q ∗ ) = p p ∗ + ϵ ( q p ∗ − p q ∗ ) . \begin{aligned} \sigma \otimes \sigma^{\diamond} &=(p+\epsilon q)\left(p^{*}-\epsilon q^{*}\right) \\ &=p p^{*}+\epsilon\left(q p^{*}-p q^{*}\right) . \end{aligned} σ⊗σ⋄=(p+ϵq)(p∗−ϵq∗)=pp∗+ϵ(qp∗−pq∗). The product is a dual quaternion whose real part is a scalar and dual part is a vector.
For each of the three introduced conjugates, the conjugate of the conjugate of σ \sigma σ is σ \sigma σ itself. The conjugate of the product of dual quaternions equals the product of the individual conjugates of these dual quaternions in the reverse order. This is established below for all three conjugates:
( σ 1 ⊗ σ 2 ) ∙ = ( p 1 p 2 + ϵ ( p 1 q 2 + q 1 p 2 ) ) ∙ = p 1 p 2 − ϵ ( p 1 q 2 + q 1 p 2 ) = ( p 1 − ϵ q 1 ) ( p 2 − ϵ q 2 ) = σ 1 ∙ ⊗ σ 2 ∙ ; \begin{aligned} \left(\sigma_{1} \otimes \sigma_{2}\right)^{\bullet}&=\left(p_{1} p_{2}+\epsilon\left(p_{1} q_{2}+q_{1} p_{2}\right)\right)^{\bullet} \\ &=p_{1} p_{2}-\epsilon\left(p_{1} q_{2}+q_{1} p_{2}\right) \\ &=\left(p_{1}-\epsilon q_{1}\right)\left(p_{2}-\epsilon q_{2}\right) \\ &=\sigma_{1}^{\bullet} \otimes \sigma_{2}^{\bullet} ; \end{aligned} (σ1⊗σ2)∙=(p1p2+ϵ(p1q2+q1p2))∙=p1p2−ϵ(p1q2+q1p2)=(p1−ϵq1)(p2−ϵq2)=σ1∙⊗σ2∙;
( σ 1 ⊗ σ 2 ) ∗ = ( p 1 p 2 + ϵ ( p 1 q 2 + q 1 p 2 ) ) ∗ = ( p 1 p 2 ) ∗ + ϵ ( p 1 q 2 + q 1 p 2 ) ∗ = ( p 1 p 2 ) ∗ + ϵ ( ( p 1 q 2 ) ∗ + ( q 1 p 2 ) ∗ ) = p 2 ∗ p 1 ∗ + ϵ ( q 2 ∗ p 1 ∗ + p 2 ∗ q 1 ∗ ) = ( p 2 ∗ + ϵ q 2 ∗ ) ( p 1 ∗ + ϵ q 1 ∗ ) = σ 2 ∗ ⊗ σ 1 ∗ \begin{aligned}\left(\sigma_{1} \otimes \sigma_{2}\right)^{*}&=\left(p_{1} p_{2}+\epsilon\left(p_{1} q_{2}+q_{1} p_{2}\right)\right)^{*}\\ &=\left(p_{1} p_{2}\right)^{*}+\epsilon\left(p_{1} q_{2}+q_{1} p_{2}\right)^{*}\\ &=\left(p_{1} p_{2}\right)^{*}+\epsilon\left(\left(p_{1} q_{2}\right)^{*}+\left(q_{1} p_{2}\right)^{*}\right)\\ &=p_{2}^{*} p_{1}^{*}+\epsilon\left(q_{2}^{*} p_{1}^{*}+p_{2}^{*} q_{1}^{*}\right)\\ &=\left(p_{2}^{*}+\epsilon q_{2}^{*}\right)\left(p_{1}^{*}+\epsilon q_{1}^{*}\right)\\ &=\sigma_{2}^{*} \otimes \sigma_{1}^{*} \end{aligned} (σ1⊗σ2)∗=(p1p2+ϵ(p1q2+q1p2))∗=(p1p2)∗+ϵ(p1q2+q1p2)∗=(p1p2)∗+ϵ((p1q2)∗+(q1p2)∗)=p2∗p1∗+ϵ(q2∗p1∗+p2∗q1∗)=(p2∗+ϵq2∗)(p1∗+ϵq1∗)=σ2∗⊗σ1∗
( σ 1 ⊗ σ 2 ) ⋄ = ( p 1 p 2 + ϵ ( p 1 q 2 + q 1 p 2 ) ) ⋄ = ( p 1 p 2 ) ∗ − ϵ ( p 1 q 2 + q 1 p 2 ) ∗ = ( p 1 p 2 ) ∗ − ϵ ( ( p 1 q 2 ) ∗ + ( q 1 p 2 ) ∗ ) = p 2 ∗ p 1 ∗ − ϵ ( q 2 ∗ p 1 ∗ + p 2 ∗ q 1 ∗ ) = ( p 2 ∗ − ϵ q 2 ∗ ) ( p 1 ∗ − ϵ q 1 ∗ ) = σ 2 ∘ ⊗ σ 1 ∘ \begin{aligned} \left(\sigma_{1} \otimes \sigma_{2}\right)^{\diamond}&=\left(p_{1} p_{2}+\epsilon\left(p_{1} q_{2}+q_{1} p_{2}\right)\right)^{\diamond}\\&=\left(p_{1} p_{2}\right)^{*}-\epsilon\left(p_{1} q_{2}+q_{1} p_{2}\right)^{*}\\&=\left(p_{1} p_{2}\right)^{*}-\epsilon\left(\left(p_{1} q_{2}\right)^{*}+\left(q_{1} p_{2}\right)^{*}\right)\\&=p_{2}^{*} p_{1}^{*}-\epsilon\left(q_{2}^{*} p_{1}^{*}+p_{2}^{*} q_{1}^{*}\right)\\&=\left(p_{2}^{*}-\epsilon q_{2}^{*}\right)\left(p_{1}^{*}-\epsilon q_{1}^{*}\right)\\&=\sigma_{2}^{\circ} \otimes \sigma_{1}^{\circ} \end{aligned} (σ1⊗σ2)⋄=(p1p2+ϵ(p1q2+q1p2))⋄=(p1p2)∗−ϵ(p1q2+q1p2)∗=(p1p2)∗−ϵ((p1q2)∗+(q1p2)∗)=p2∗p1∗−ϵ(q2∗p1∗+p2∗q1∗)=(p2∗−ϵq2∗)(p1∗−ϵq1∗)=σ2∘⊗σ1∘.
边栏推荐
- MySQL5.6 (5.7-8) 基于shardingsphere5.1.1 Sharding-Proxy模式读写分离
- 2022-01-12: give a positive array arr, length N, subscript 0~n-1, a
- Topic35——34. Find the first and last positions of elements in a sorted array
- Fastdata pole | insight report on e-commerce consumption of young Chinese users 2021
- C语言 踩坑:文档编码错误,导致base64中文编码错误
- Give up Visio, this drawing tool is really fragrant!
- C# wpf 附加属性实现界面上定义装饰器
- 从 WAN 到 SD-WAN 边缘设备的网络架构
- 下载oss文件并修改文件名
- Haas 506 2.0 Tutoriel de développement - bibliothèque de composants avancés - modem. SMS (ne prend en charge que les versions supérieures à 2,2)
猜你喜欢

开源生态|超实用开源License基础知识扫盲帖(下)

Illustration Google V8 18: asynchronous programming (I): how does V8 implement micro tasks?
Link of Baidu URL parameter? Research on URL parameter encryption and decryption (code example)

射频内容学习

综合培养学生脑力思维的少儿编程

Day_ 05 smart communication health project - appointment management - appointment settings
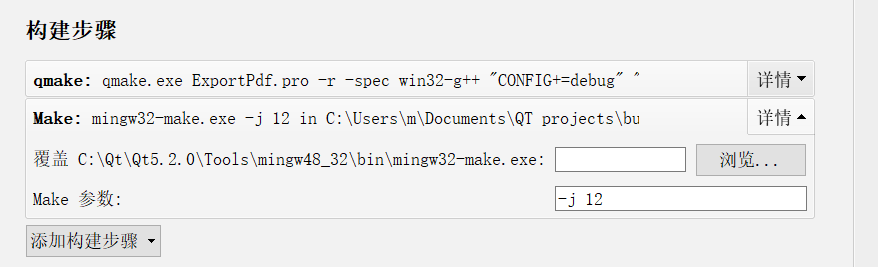
Qt使用多线程编译项目的方法

Haas 506 2.0 Tutoriel de développement - bibliothèque de composants avancés - modem. SMS (ne prend en charge que les versions supérieures à 2,2)

Softing dataFEED OPC Suite将西门子PLC数据存储到Oracle数据库中

Summary of business logic security ideas
随机推荐
2022-01-12: give a positive array arr, length N, subscript 0~n-1, a
剑指 Offer 42. 连续子数组的最大和
There are so many code comments! I laughed
开源生态|超实用开源License基础知识扫盲帖(下)
Leetcode topic resolution valid anagram
Leetcode topic resolution single number II
设计师需要懂的数据指标与数据分析模型
综合培养学生脑力思维的少儿编程
【踩坑记录】数据库连接未关闭连接,释放资源的坑
haas506 2.0开发教程-高级组件库-modem.sms(仅支持2.2以上版本)
Topic35——34. 在排序数组中查找元素的第一个和最后一个位置
疫情下的传媒产业,小程序生态驱动数字化转型探索
解析创客教育中的造物原理
haas506 2.0开发教程-高级组件库-modem.net(仅支持2.2以上版本)
haas506 2.0开发教程-高级组件库-modem.voiceCall(仅支持2.2以上版本)
Day_02 传智健康项目-预约管理-检查项管理
坐标 转化
Functions and basic structure of CPU
Day_ 09 smart health project - mobile terminal development - Mobile quick login and permission control
百度URL參數之LINK?URL參數加密解密研究(代碼實例)
