当前位置:网站首页>当今的数学是否过于繁琐?
当今的数学是否过于繁琐?
2022-06-21 06:01:00 【Channing Lewis】
当我们看到某个定理动辄几十上百页的证明时,我们不禁会思考这是这个定理最简单的证明吗?是否还有简化的空间?当今的数学理论是否像曾经的地心说,使用繁琐的过程贴近某个可以用更简单的方式理解的事实?
这似乎涉及到数学是发明还是发现的问题——如果是发明,那么肯定有改进的空间;如果是发现,那它就是事实本身,不能再简化。然而,即使数学是发现,也会有不同的理解方式,就像同一个物理现象有不同的解释一样。
如果当今的数学不是最优的理解方式,那么很可能会出现一次革命性简化,这会以什么方式出现?是当数学发展到一定阶段,人类对数学的繁琐忍无可忍,最终诞生一位“哥白尼”?还是一位没有受过目前的数学教育的数学天才,自我推导出一种全新的数学?或者是人工智能发展到一定阶段,自我领悟出了数学的真谛?甚至于,人类遇到外星文明,发现它们的数学更加简化而采纳……
需要注意的是,不管是哪种情况,这场革命必然不会那么顺利,我们不能忘记“日心说”的历史。当一种新的数学出现时,即使能够给出更高效、更合理的解释,也会受到顽强的守旧派的怀疑、攻击。在人类目前的数学教育体系下,更简化的数学要出现是非常困难的。因为每一个孩子从小接受的都是同一套数学,这套数学被我们当成了理解数学世界的最佳方式,等到孩子长大以后想提出不同的思想时,传统数学的观念已经根深蒂固了。因此,只有两种情况可以突破这种限制:一是孩子是一个神童,在接受传统数学之前就建立了自己的数学体系;二是孩子在学习传统数学时能够保持自己的想法,忍受误解、嘲讽,最终取得成功。那么有没有可能改变目前的数学教育体系,允许孩子从小就接受不同的数学思想呢?当然是可能的,只是推行比较困难,因为有能力推动变革的人都是深受传统数学影响的人,甚至可以说是既得利益者,推动变革的意愿和动力不足。这就成为了一个死循环。
数学的革命性简化的突破口一定是非常基础的,否则在传统的数学大厦上想要建立起全新的理论是几乎不可能的。这场革命很可能和一些本质问题有关,例如“数的本质是什么”、“计算的本质是什么”、“空间的本质是什么”……即使是目前的顶尖数学家对这些千年难题的回答也只是见仁见智、盲人摸象而已,还没有一个公认的、可以深刻改变人类对世界的理解的答案。
一旦数学实现了革命性简化,一些以数学为基础的领域将会跟着产生突破,例如通用人工智能和基础物理。我们知道现在的人工智能都是专用的,需要针对某个领域专门编写程序,事实上肯定存在一种通用程序,经过简单的调整就能够适用于任何场景,这也是人工智能从诞生开始就设定的目标,但是从1956年到现在,迟迟都没有突破,甚至可以说没有实质性进展,这和当今数学的局限性有很大关系。同样的,基础物理也已经几十年没有突破性进展了,虽然原因是多方面的,但是和当今数学的滞后有很大关系。
当今的数学肯定不是最优的数学,革命肯定会到来,我们要做的是保持开放的心态,不能把当今的数学奉若神明。
转载于公众号:智能探索
边栏推荐
- Aurora8b10b IP usage-03-ip configuration application guide
- 397 linked list (206. reverse linked list & 24. exchange nodes in the linked list in pairs & 19. delete the penultimate node of the linked list & interview question 02.07. link list intersection & 142
- 直击2022互联网大裁员:繁花落地,一地鸡毛
- 平衡二叉树详解 通俗易懂
- FPGA - 7系列 FPGA SelectIO -02- 源语简介
- NumPy的广播机制
- 5254. 卖木头块 动态规划
- tf. compat. v1.MetaGraphDef
- Construction and protection of small-scale network examination
- nametuple的源码为什么要使用.replace(‘,‘, ‘ ‘).split()而不是.split(‘,‘)
猜你喜欢

模块 14 - 15:网络应用通信考试
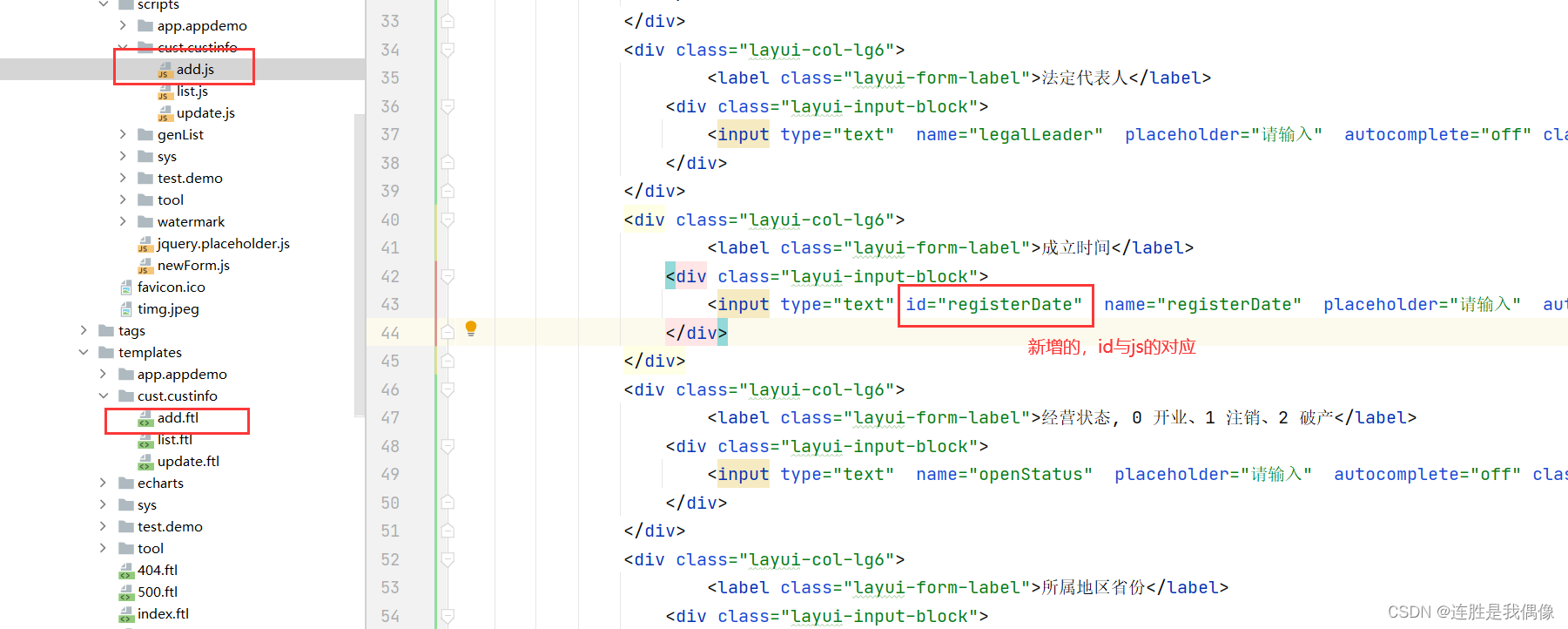
The time plug-in is used for the establishment time, but when modifying parameters on the web page, if the time is not modified, an error will be reported when saving it for the first time, and it can

FPGA - 7系列 FPGA SelectIO -02- 源语简介

FPGA - 7系列 FPGA SelectIO -06- 逻辑资源之ODELAY

【数据挖掘】期末复习 第五章
![Leetcode 75 - three implementation methods of color classification [medium]](/img/52/61ae051babf6b5c6b603093a17e55c.png)
Leetcode 75 - three implementation methods of color classification [medium]

深度理解RNN的梯度消失和LSTM为什么能解决梯度消失

正则表达式基础

sqli-labs25

contos7 安装svn服务端
随机推荐
tf.AUTO_REUSE作用
Aurora8B10B IP使用 -03- IP配置应用指南
【你所熟悉的网络真的安全吗?】万字文
sqli-labs-17
【MYSQL】MySQL的SQL语句执行流程
Do you want to manually implement CSDN dark mode for web page '?
【【毕业季·进击的技术er】------老学长心得分享
FPGA - 7系列 FPGA SelectIO -03- 逻辑资源之ILOGIC
BN的一些细节
数字信号处理-07-DDS IP应用实例
第二章:数据模型(数据库期末复习)
scala中函数和方法
Gpushare- members are coming online~
上手自定义线程池
tf.compat.v1.get_default_graph
内卷大厂系列《LRU 缓存淘汰算法》
C language course design (detailed explanation of clothing management system)
xshell7远程连接服务器,挂起进程一直维持程序的运行
DDD 实践手册(4. Aggregate — 聚合)
微生物生态数据分析——冗余分析