当前位置:网站首页>第六章——分枝限界法
第六章——分枝限界法
2022-06-10 22:14:00 【酉鬼2333】
分枝限界法概述
分枝限界法和回溯法一样,也是一种在问题的解空间树上搜可行解的穷举算法。
其中“分枝”指的是“分枝限界法”搜索可行解采用的策略为广度优先搜索或实现方法和思路类似的代价优先搜索。
广度优先搜索的概念和实现前面已经介绍过很多次了,这里不再做赘述;代价优先搜索的目的是以某种定义下的优先级,按照优先级从高到低的顺序处理所有的结点。
(从低到高和从高到低本质上是一样的,这里以从高到低为例)。
如果状态结点能够按照优先级不严格(可以相等)降低的顺序,在解空间树上按照结点高度从高到低,同高度结点从左到右或从右到左的排列,那我们可以用广度优先搜索来达到代价优先搜索的目的(广度优先搜索的搜索顺序和代价优先搜索的搜素顺序相同)。
但是状态空间树上的状态结点是通过决策联系起来的,决策对于状态优先级相关的属性的变化多样(可能增大,可能减小,可能线性,可能非线性),状态结点按照优先级从高到低的顺序在状态空间树上的出现往往会是跳跃式的,与解空间树的结构无关。
如果策略能够始终保持状态结点到子节点优先级相关的属性递增或递减(即树上的结点从属性数值的角度来看符合堆的性质),我们可以在代价优先搜索中用堆数据结构来存储状态空间中未处理过的结点,处理节点过程中根据可选策略扩展结点加入容器的方法和广度优先搜索相同。
根据堆数据结构的性质,我们每次取堆顶(队首)结点进行处理,即是剩余未处理结点中优先级最高的结点(未加入容器的子孙节点,容器中一定存在一个结点的优先级高于该子孙节点的优先级,所以是未处理中结点中优先级最高的结点),这样一直处理即是按照优先级最高到低的顺序处理所有的状态节点。
(具体原因和用反证法证明,不做赘述)。
“限界”指的是限界函数,和回溯法中的限界函数一样,在广度(代价)优先搜索将被扩展的结点加入到(优先)队列中时,删除掉一些不必要的子节点,从而将选择变得更有效以加速搜索的进程。
个人归纳认为:回溯法=(状态空间树上的)一般深度优先搜索+限界函数,分枝限界法=(状态空间树上的)一般广度(代价)优先搜索+限界函数。
作为两种在状态空间书上搜索可行解的算法,我们一般考虑状态空间树的宽度和深度来选择使用回溯法还是分枝限界法:存在根节点到部分叶子结点的路径过长时,选择分枝限界法避免进入某条过长路径的搜索;如果可选择的决策过多,即树的宽度过大时,选择回溯法来避免扩展状态空间树同一高度过多的状态节点。
如果两种情况同时存在,可以采取限定单次回溯法搜素最大深度的方法来避免回溯法搜素进入过深的分支,不断扩大单次回溯法搜素的最大深度直到某次的回溯法寻找到可行解为止,这种策略称为迭代加深。
如果状态节点的属性满足代价优先搜索的要求,即子节点的优先级都高于父节点的优先级,我们也可以用分枝限界法去寻找特定意义上的最优解。
如果属性值(优先级)按照层次从上到下递减且最优解的“优”指的就是按照层次从上到下递减的优先级,那么以代价优先搜索为模板搜素到的第一个可行解即为我们的最优解,在这种问题背景下不需要进行与当前最优解比较判断能否得到更优解的剪枝函数。
确定可行解(最优解)所进行的决策
即在图(树)的搜索问题中,求解根结点到当前结点的路径,一般有两种通用的策略:
第一种是对每个节点保存根节点到该节点的路径,在扩展时通过根结点到父节点的路径获得根结点到子节点的路径。
这种方法实现起来简单,但是往往会浪费空间和时间。
第二种是在扩展子节点时对每个结点保存它在状态空间上的前驱节点,即父节点,然后通过对父节点的回溯得到该节点到根节点的路径,逆序即是根节点到该节点的路径。
分枝限界法的时间性能
分枝限界法和回溯法本质上都属于穷举法(广度优先搜索和深度优先搜索),在最坏情况下与穷举法的复杂度相同(甚至更糟,因为需要进行限界值的计算和限界函数的判断),实际求解效率基本上由限界函数决定。
求解0/1背包问题
即前面介绍过很多遍的0/1背包问题。
重量小于规定重量的结点通过决策构成解空间树,由于0/1背包问题的决策保证子节点中的价值属性一定大于等于父节点的价值属性,结点的价值属性用于确定结点的优先级,我们可以通过优先队列式分枝限界法,即以代价优先搜索为模板的分枝限界法求解0/1背包问题的最优解。
代价预先搜索求解0/1背包问题,就是在解空间树上以状态节点的价值属性作为优先级高度的标准进行上的代价优先搜索。
限界函数中的左孩子剪枝策略与回溯法中的左孩子剪枝策略一致;上一章节中提到0/1背包的右孩子剪枝相当于固定右子节点后续的策略向左,即将所有还没有选择的物品加入背包来得到一个价值的上界。
实际上这种价值上界的估计是比较粗糙的,因为剩余的物品我们往往无法全部加入到当前的背包中。这种上界估计的方式就相当于固定策略跳跃到右子树最左边的状态节点,没有进行真正的搜索,实际上这个扩展得到的“最左边的状态节点”可能并不满足问题规范的条件,即不是一个满足要求的可行解(实际不存在于解空间树上),上界被估计得过高了。
那如果我们是通过实际搜索,搜索到右子树满足问题条件的最左状态节点呢?即课件上的原做法:

这种价值上界的估计方法在重量小价值高的物品出现在解空间树下层的决策时会出现反例。解决的方案也很简单,就是避免重量小价值高的物品出现在解空间树的下层,或者说避免重量小价值高的物品在物品序列中出现在重量大价值小的物品之后,即对物品序列进行一个预处理:在进行分枝限界法之前,先按照“价值/重量”的值对物品序列进行从大到小的排序。
对应的队列式分枝限界法求解如下(只介绍一个框架,在能够使用代价优先搜索的情况下一般还是使用代价优先搜索):
//队列中的状态结点类型
struct NodeType{
int no;//结点编号
int i;//当前结点在搜索空间中的层次
int w;//搜素到当前结点的总重量
int v;//搜素到当前结点的总价值
int x[MAXN];//搜素到当前状态结点进行过的决策
double ub;//限界函数bound预估的价值上界
};
//计算状态结点e的价值上界
//需要对物品价值/重量的值进行一个排序
void bound(NodeType &e){
//固定后续的决策向左,搜索右子树满足问题条件的最左状态节点
int i=e.i+1;
int sumw=e.w;
double sumv=e.v;
while ((sumw+w[i]<=W)&&i<=n){
sumw+=w[i]; sumv+=v[i]; i++;
}
//如果所有剩余的物品不能全部装入背包,对于不能完全装入背包的物品,采用分块极限的方式估计价值上界
if (i<=n) e.ub=sumv+(W-sumw)*v[i]/w[i];
//如果所有剩余的物品都能装入背包
else e.ub=sumv;
}
//将结点加入容器并通过结点的层次判断可行解,通过比较得到最优解
void EnQueue(NodeType e,queue<NodeType> &qu){
//通过结点的层次判断可行解
if (e.i==n){
if (e.v>maxv){
//保存最优解的信息
maxv=e.v;
for (int j=1;j<=n;j++) bestx[j]=e.x[j];
}
}
else qu.push(e);//非叶子结点进队
}
//队列式分枝限界法求0/1背包的最优解
void bfs(){
int j;
NodeType e,e1,e2;
queue<NodeType> qu;//定义一个队列
//根结点置初值
e.i=0; e.w=0; e.v=0; e.no=total++;
for (j=1;j<=n;j++) e.x[j]=0;
bound(e);//计算根结点的价值上界
qu.push(e);//根结点进队
while (!qu.empty()){
//对队首结点进行不同的决策进行扩展
e=qu.front(); qu.pop();
//左孩子剪枝
if (e.w+w[e.i+1]<=W){
//建立左孩子结点
e1.no=total++;
e1.i=e.i+1; e1.w=e.w+w[e1.i]; e1.v=e.v+v[e1.i];
//复制决策
for (j=1;j<=n;j++) e1.x[j]=e.x[j];
e1.x[e1.i]=1;//添加新的决策
bound(e1);//求左孩子结点的价值上界
EnQueue(e1,qu);//左孩子结点进队
}
//建立右孩子结点
e2.no=total++;
e2.i=e.i+1; e2.w=e.w; e2.v=e.v;
//复制决策
for (j=1;j<=n;j++) e2.x[j]=e.x[j];
e2.x[e2.i]=0;//添加新的决策
//计算右孩子节点的价值上界进行右孩子剪枝
bound(e2);
if (e2.ub>maxv){
EnQueue(e2,qu);//右孩子结点进队
}
}
}
优先队列式分枝限界法和队列式分枝限界法实现上的区别就是:
1.容器为优先队列。
2.需要结构体的定义中重载关系函数保证优先队列能够应用(0/1背包问题中按照当前装入背包的价值排序)。
优先队列式分枝限界法的求解过程不做赘述。
无论采用队列式分枝限界法还是优先队列式分枝限界法求解0/1背包问题,最坏情况下都要搜索整个解空间树,所以最坏时间和空间复杂度均为O(2n),其中n为物品个数。
求解任务分配问题
即还是前面介绍过的任务分配问题。
任务分配对应的解空间树为排列树,从根节点开始的第i次决策表示给第i个人分配任务。我们考虑当前已经分配了的任务的代价之和属性,由决策得到的子节点的代价之和一定大于父节点的代价之和,于是我们可以使用优先队列式分枝限界法处理这个问题。
代价预先搜索求解任务分配问题,就是在解空间树上以状态节点的代价属性作为优先级高度的标准进
行代价优先搜索。
代价之和从上到下递增,而我们想要求的是可行解(进行了n次决策的叶子节点)中代价之和最小的结点,所以优先队列式分枝限界法搜索到的第一个可行解即是我们需要的代价之和最小的最优解,不需要与当前最优解进行比较判断能否得到更优解。
(但我们还是学习一下剪枝函数的设计方法)
那么能否进行剪枝呢?虽然上一章节没有对这个问题进行介绍(因为认为任务分配问题不应该用子集树的框架去处理而是该用排列树的框架去处理),但我们仍然能得到一个简单的剪枝方法:
对于某个状态节点,将它的代价值与目前的最小代价进行比较,如果代价值大于目前的最小代价,那么就没有必要对该子树进行搜索。
这种剪枝方法尝试估计从该节点向下搜索的价值下界(后面简称价值下界),但和前面未优化的右孩子剪枝策略一样,对于下界的估计过于粗略。
一种优化的估计策略是:不管后续的选择之间是否会发生冲突,给后面每个人分配他们除去当前状态已经分配过的任务以外代价最低的任务,来估算代价的下界。
这样估计是否能够保证为代价的下界呢?显然是可以的,因为对于任意一种分配方案每一个人实际选择的任务的代价都要大于等于上述估计策略给他分配的任务代价,所以上述策略分配的代价之和一定小于等于实际的最小代价。
这也是一种常见的剪枝函数的设计方法:违反整体规则的各局部最优设计方法(注意不是违反整体最优)。
(如果在估计时避免后续的选择发生冲突,那么就是一个贪心策略得到的局部最优方案,不一定能够得到整体的最优,更别说用来做下界估计了)
对应的优先队列式分枝限界法如下(含与当前最优解比较的剪枝函数):
//状态结点类型
struct NodeType{
int no;//结点编号
int i;//当前结点在搜索空间中的层次,即人员编号
int x[MAXN];//x[i]为第i层给人员i分配的任务编号
bool worker[MAXN];//worker[i]=true表示任务i已经分配
int cost;//已经分配的任务所需要的成本
int lb;//代价下界
//重载<关系函数
//通过cost进行比较而不是代价下界
bool operator<(const NodeType &s) const{
return cost>s.cost;
}
};
//计算状态结点的代价下界
void bound(NodeType &e){
int minsum=0;
//不管后续的选择之间是否会发生冲突
//给后面每个人分配他们除去当前状态已经分配过的任务以外代价最低的任务
for (int i1=e.i+1;i1<=n;i1++ ){
int minc=INF;
for (int j1=1;j1<=n;j1++)
if (e.worker[j1]==false&&c[i1][j1]<minc) minc=c[i1][j1];
minsum+=minc;
}
//估计得到当前状态结点向下搜索的最小代价
e.lb=e.cost+minsum;
}
//优先队列式分枝限界法求解任务分配问题
void bfs(){
int j;
NodeType e,e1;
priority_queue<NodeType> qu;
memset(e.worker,0,sizeof(e.worker));
//初始化根节点
e.i=0; e.cost=0; bound(e); e.no=total++;
memset(e.x,0,sizeof(e.x));
qu.push(e);//根结点进队列
while (!qu.empty()){
e=qu.top(); qu.pop();
//第一达到经过n次决策的可行解,即是我们想要的代价最低的可行解
//(因为是按照代价从低到高搜索的)
if (e.i==n){
for (j=1;j<=n;j++) bestx[j]=e.x[j];
}
e1.i=e.i+1;//扩展分配下一个人员的任务
for (j=1;j<=n;j++){
if (e.worker[j]) continue;//考虑没有分配过的任务
//复制已经分配过的任务
for (int i2=1;i2<=n;i2++) e1.worker[i2]=e.worker[i2];
//复制给哪些人分配了哪些任务
for (int i1=1;i1<=n;i1++) e1.x[i1]=e.x[i1];
e1.x[e1.i]=j;//给第i个人分配第j个任务
e1.worker[j]=true;//表示任务j已经分配
e1.cost=e.cost+c[e1.i][j];
e1.no=total++;
bound(e1);//估计代价下界,进行剪枝
if (e1.lb<=mincost) qu.push(e1);
}
}
}
求解流水作业调度问题
即上一章节的流水作业调度问题。
根据上一章节的分析,流水作业调度问题的解空间树也为排列树,从根节点开始的第i次决策表示给第i轮分配需要加工的作业。我们考虑状态节点M1和M2处理完当前分配的任务的时长之和属性,由决策得到的子节点的时长之和一定大于父节点的时长之和,于是我们可以使用优先队列式分枝限界法处理这个问题。
代价预先搜索求解流水作业调度问题,就是在解空间树上以状态节点的时长属性作为优先级高度的标准进行代价优先搜索。
时长之和从上到下递增,而我们想要求的是可行解(进行了n次决策的叶子节点)中时长之和最小的结点,也就是说仍然可以直接确定最优解,不需要通过与当前最优解的比较进行剪枝。
(但我们也还是学习一下剪枝函数的设计方法)
和前面问题一样,能够得到最粗糙的剪枝法:将状态结点的执行时长属性与最优解的时长进行比较。
那么有没有优化的设计方案呢?
固定决策的方向得到只是一种可行解,得到的值无法作为下界的估值,考虑违反整体规则的各局部最优设计方法。
但是我们这里的每个任务无论放在第几个加入流水线,它需要加工的时间都是一样的,即不存在一个选择让局部最优。
那指的是什么最优呢?对于一次决策我们实际上希望避免出现的情况是糟糕的分配方案导致M2需要等待M1工作完再进行工作,即每一次决策都只需要计算M2加工作业的时间(M2始终有事可做,没有进入闲置的状态)。
那么优化的下界估价函数,就是保证后面所有还没有分配的任务,M2都是立即完成的,即在当前状态节点的时长之和加上剩余作业在M2上需要进行的时间来估计完成所有作业的时长下界。
对应的算法如下(含与当前最优解比较的剪枝函数):
//状态节点类型
struct NodeType{
int no;//结点编号
int x[MAX];//x[i]表示第i次决策分配进流水线的作业编号
int y[MAX];//y[i]=1表示编号为i的作业已经分配
int i;//进行到的决策编号,即当前结点在搜索空间中的层次
int f1;//已经分配作业在M1的执行时间
int f2;//已经分配作业在M2的执行时间
//前一章节的结论如下:
//f1=f1+a[j];
//f2[i]=max(f1,f2[i-1])+b[j]
int lb;//时长下界
//重载<关系函数
bool operator<(const NodeType &s) const{
return f2>s.f2;//通过M2执行完当前任务分配的时间进行比较
};
//计算状态结点的代价下界
void bound(NodeType &e){
//在当前状态节点的时长之和
//加上剩余作业在M2上需要进行的时间来估计完成所有作业的时长下界
int sum=0;
for (int i=1;i<=n;i++) if (e.y[i]==0) sum+=b[i];
e.lb=e.f1+sum;
}
//求优先队列式分枝限界法解流水作业调度问题
void bfs(){
NodeType e,e1;
priority_queue<NodeType> qu;
//初始化根节点信息
memset(e.x,0,sizeof(e.x));
memset(e.y,0,sizeof(e.y));
e.i=0; e.f1=0; e.f2=0;
e.no=total++;
bound(e);//计算根节点的时长下界
qu.push(e);//根结点进队列
while (!qu.empty()){
e=qu.top(); qu.pop();
//第一达到经过n次决策的可行解,即是我们想要的时长最低的可行解
//(因为是按照时长从低到高搜索的)
if (e.i==n){
for (int j1=1;j1<=n;j1++) bestx[j1]=e.x[j1];
}
e1.i=e.i+1; //扩展分配下一个作业
for (int j=1;j<=n;j++){
if (e.y[j]==1) continue;//考虑未分配的作业
//复制每一步之前分配的哪些作业
for (int i1=1;i1<=n;i1++) e1.x[i1]=e.x[i1];
//复制已经分配过的作业的编号
for (int i2=1;i2<=n;i2++) e1.y[i2]=e.y[i2];
e1.x[e1.i]=j;//为第i步分配作业j
e1.y[j]=1;//表示作业j已经分配
e1.f1=e.f1+a[j];//f1=f1+a[j]
e1.f2=max(e.f2,e1.f1)+b[j];//f2[i+1]=max(f2[i],f1)+b[j]
bound(e1);//计算下界进行剪枝
if (e1.f2<=bestf){
e1.no=total++;
qu.push(e1);
}
}
}
}
总结
代价优先搜索适用于子节点的值(优先级)比父节点的值(优先级)高的树,可以对解空间树上的状态结点按照优先级从高到低(从低到高)的顺序进行搜素。
回溯法=一般深度优先搜索+限界函数。
分枝限界法=一般广度(代价)优先搜索+限界函数。
当分枝限界法的模板为代价优先搜索时,按照优先级从高到低进行搜索时,我们搜索到的第一个可行解即为优先级最低的可行解,如果优先队列中的优先级与我们需要的优先级恰好相反,那代表我们已经得到了我们需要的最优解,这时候就不需要与当前最优解比较判断能否得到更优解的剪枝函数了。
边栏推荐
- Why is the video fusion cloud service easycvr cluster video event query invalid?
- Software features and functions of the blind box mall app system development
- DC2 of vulnhub
- Redis数据结构
- Executor - Shutdown、ShutdownNow、awaitTermination 詳解與實戰
- Vscode common shortcuts
- vulnhub之dc3
- 上海股票开户是安全的吗?
- Auto. JS Pro development environment configuration
- 期货开户有什么限制嘛?哪里最安全?
猜你喜欢

Vscode common shortcuts

Lenovo explained for the first time the five advantages of hybrid cloud Lenovo xcloud and how to build an intelligent digital base

原生支持 ARM64 的首个版本!微软 Win11/10 免费工具集 PowerToys 0.59 发布
![[论文分享] PATA: Fuzzing with Path Aware Taint Analysis](/img/f6/627344c5da588afcf70302ef29d134.png)
[论文分享] PATA: Fuzzing with Path Aware Taint Analysis

2022g1 industrial boiler stoker test questions and online simulation test
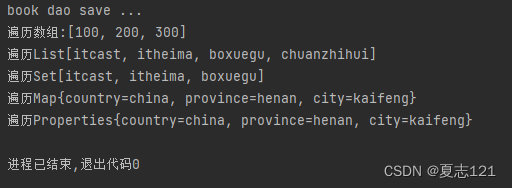
Array, list, set, map, properties dependency injection format

PwnTheBox,Web:hello

Development and implementation of AI intelligent video analysis easycvr platform device channel batch deletion function

Introduction to software testing: the concept and process of software testing (brilliant content)

盲盒商城APP系统开发的软件特点和盲盒功能介绍
随机推荐
Introduction to software testing: the concept and process of software testing (brilliant content)
HALCON联合C#检测表面缺陷——仿射变换(二)
Vulnhub练习 DC-1靶机
Optimize code to remove if else
Gather for summer Yiping: not everything is reported to Robin Lee. They compete with Xiaomi Huawei by products
数组、List、Set、Map、Properties依赖注入格式
项目实训11——对数据库的定时备份
Basic SQL statement - insert
IPO can't cure Weima's complications?
Sealem Finance-基于Web3的全新去中心化金融平台
unity 代码为动画注册事件
Project training 13 - Interface supplement
MySQL MVCC 多版本并发控制
爬虫学习知识
DependencyManagement 和 Dependencies
Creation of thread pool
Ribbon负载均衡策略
JS sensitive information leak detection tool
数据与信息资源共享平台(七)
Untiy reset animation