浅层了解欧拉函数

基础知识

根据算数基本定理：任何一个大于1的自然数 N,如果N不为质数，那么N可以唯一分解成有限个质数的乘积，即 $N={p_1}^{{\alpha }_1}{p_2}^{{\alpha }_2}...{p_n}^{{\alpha }_n}$， 其中 $p_1、p_2、...、p_n$ 称为N的质因数
$eg:12=2\ast 2\ast 3=2^2\ast 3$

欧拉函数

通式：$\phi (n)=n(1-\frac{1}{p_1})(1-\frac{1}{p_2})...(1-\frac{1}{p_n})$，这里的 $p_1、p_2、...、p_n$ 也就是上面基础知识所介绍的质因数。
欧拉函数解决的是小于n的正整数中与n互质的数的数目问题，因此 $\phi (1)=1$。
$eg:$由 $12=2\ast 2\ast 3=2^2\ast 3$，得 $\phi (12)=12\ast (1-\frac{1}{2})\ast (1-\frac{1}{3})=4$ 。
我们列举小于12的正整数，1、2、3、4、5、6、7、8、9、10、11，发现与12互质的数字是 1、5、7、11，正好是4个，这也侧面说明了欧拉函数的正确性。

实现代码

//求一个数的欧拉函数值
int Euler(int n){
    
    int phi=n;
//为什么i只需要到sqrt(n)呢？因为两个大于sqrt(n)的数相乘就会大于n。
    for(int i=2;i*i<=n;++i){
    
        if(n%i==0)phi=phi/i*(i-1); //找到质因数i
        while(n%i==0)n/=i; //消去i
    }
    if(n>1)phi=phi/n*(n-1); //特判
    return phi;
}

//区间预处理欧拉函数
void euler(int n){
    
    for(int i=1;i<=n;++i)Phi[i]=i; //假设i是质数
    for(int i=2;i<=n;++i){
    
        if(Phi[i]==i){
     //Phi[i]==i说明i是质数
            for(int j=i;j<=n;j+=i){
    
                Phi[j]=Phi[j]/i*(i-1);
            }
        }
    }
}

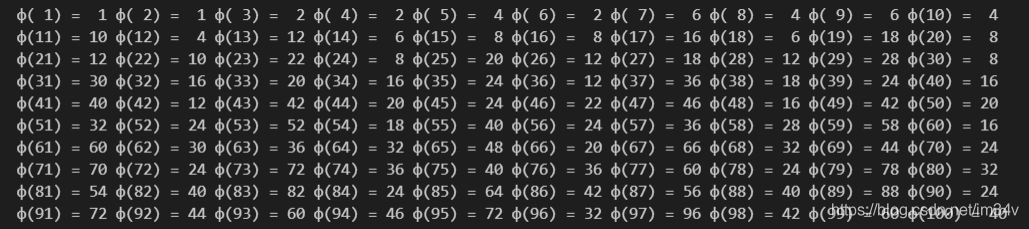
欧拉函数的性质

通过代码的运行结果，我们可以发现欧拉函数的一些性质：（不严谨但是直观）
1、n为质数时，$\phi (n)=n-1$
2、n为奇质数时，$\phi (2n)=\phi (n)$

积性函数

积性函数指对于所有互质的整数a和b有性质 $f(ab)=f(a)f(b)$ 的数论函数，其中欧拉函数就属于积性函数，即 $gcd(m,n)==1时，\phi (mn)=\phi (m)\phi (n)$。