A simple understanding of hill ordering

Detailed description

Hill sort is also called reduced incremental sort , It mainly groups the sequences according to a certain increment of subscript , Sort each group using the direct insertion sort algorithm ; As the increment decreases , Each group contains more and more keywords , When the increment is reduced to 1 when , The whole document is just a group , The algorithm terminates .

The detailed execution steps of hill sorting are as follows ：

1. Select a sequence of deltas t1, t2, ..., tk, among ti > tj,tk = 1;
2. By incremental sequence number k Proceeding on sequence k Trip to sort ;​​
3. Every trip to sort , According to the corresponding increment ti The sequence to be sorted is divided into several pieces of length m The subsequence , Direct insertion sort is performed on each subtable respectively ;
4. The incremental factor is only 1 when , The entire sequence is treated as a table , The table length is the length of the entire sequence .

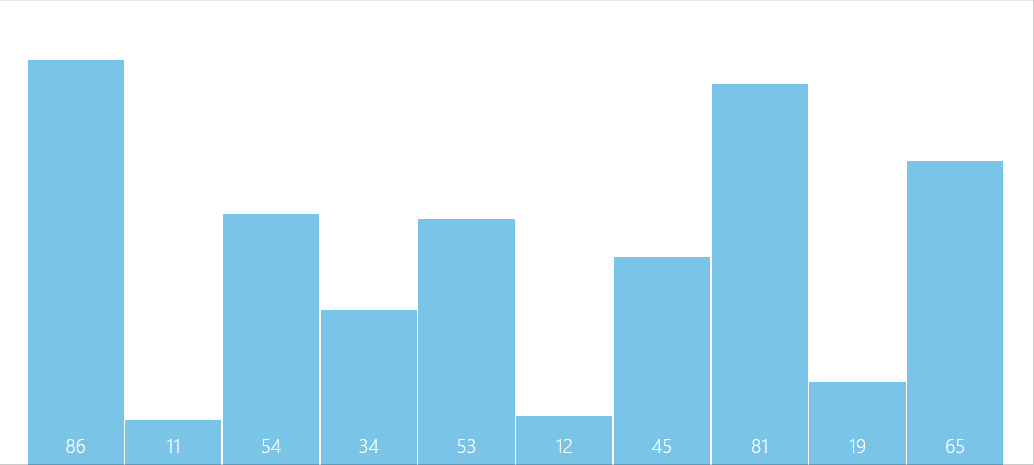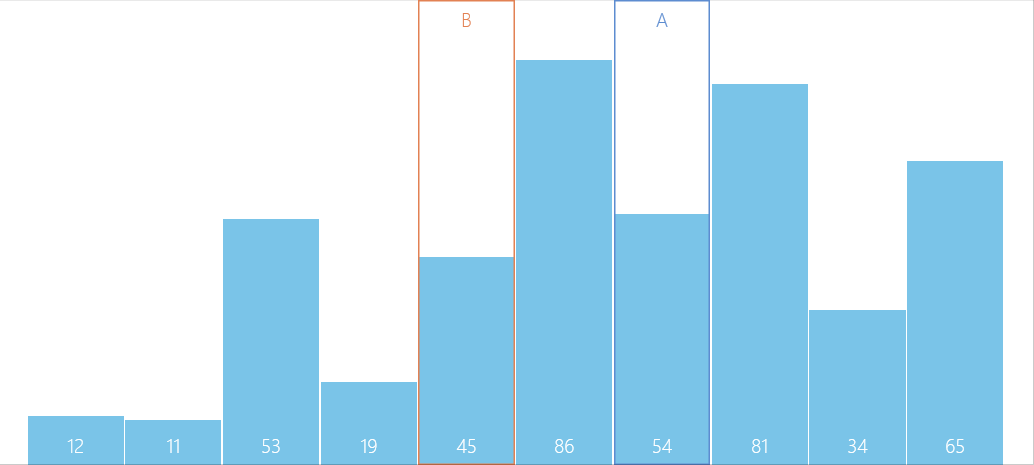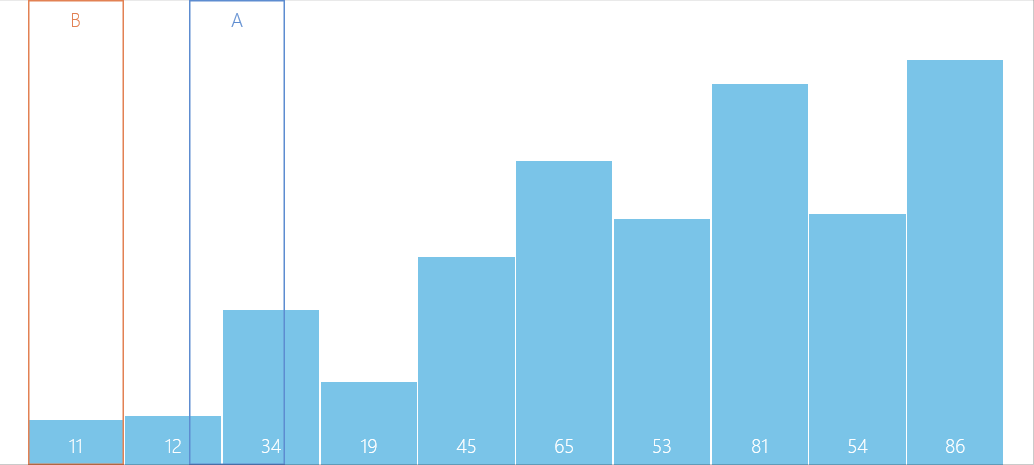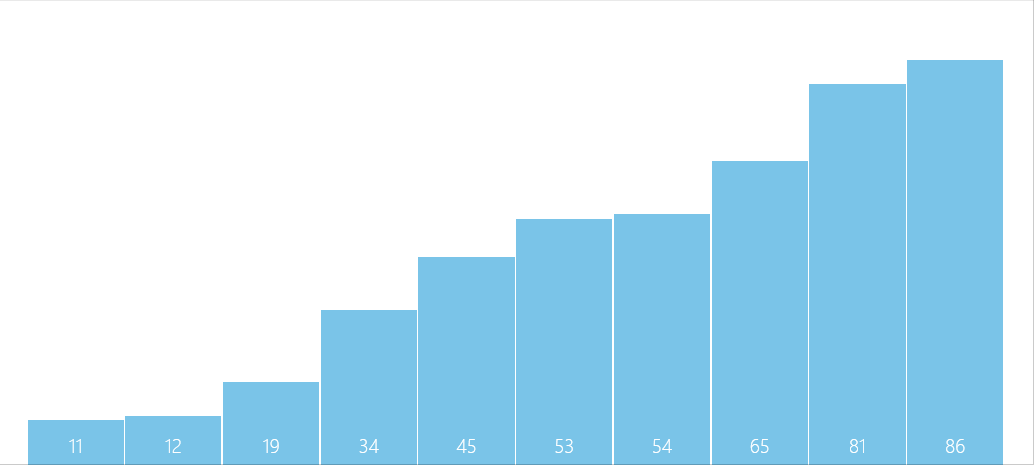
Algorithm diagram

Problem solving

Is Hill sort in place ?

Hill sort is an optimized version of insert sort , Use an optimized strategy to use insert sorting , Increase of efficiency , No extra memory space is used , So Hill sort is a sort in place algorithm .

Is Hill sort a stable sort algorithm ？

Insert sort is a stable sort algorithm , however , Because Hill sort uses incremental intervals for insert sort , Hill sort is not as stable as insert sort , In the sorting process, there will be two equal numbers with different order .

What is the time complexity of hill sorting ？

The best time complexity is \(O(n)\); The worst case time complexity is \(O(n^2)\); Because the time spent in Hill sorting is also determined by the increment interval , The average time complexity is not clear , The average time complexity can be seen as \(O(n^{1.3 \sim 2})\).

Code implementation

package cn.fatedeity.algorithm.sort;

/**
 *  Hill sort algorithm 
 */
public class ShellSort {
    public static int[] sort(int[] numbers) {
        int length = numbers.length;
        //  Usually, the incremental sequence is bisected to split the original sequence 
        for (int gap = length >> 1; gap > 0; gap = gap >> 1) {
            for (int i = gap; i < length; i++) {
                int j = i, current = numbers[i];
                while (j >= gap && numbers[j - gap] > current) {
                    numbers[j] = numbers[j - gap];
                    j = j - gap;
                }
                numbers[j] = current;
            }
        }
        return numbers;
    }
}