当前位置：网站首页>Leetcode bit operation

Leetcode bit operation

2022-07-03 10:04:00 【Σίσυφος one thousand and nine hundred】

An operation , Learn to forget , Brush questions and learn , Can't remember , Maybe I haven't learned the essence , Go ahead ！

Original code / Inverse code / Complement code

Inverse code ：

If it's a positive number , Original code = Inverse code ;
If it's a negative number , take 0 Turn into 1,1 Turn into 0, The sign bit is fixed （ The fixed sign here means that the sign bit cannot be 1 Turn into 0）
Complement code ：
If it's a positive number , Original code = Inverse code = Complement code ;
If it's a negative number , Add the inverse code 1 operation , The sign bit is fixed （ The fixed sign bit here means that when changing from inverse code to complement code , Sign bits do not participate in carry operations , Do not participate in borrow operation when changing from complement to inverse ）
8 Source code ： 0000000000000000000000000000 1000
-8 The original code of ：1000000000000000000000000000 1000
-8 The inverse of ：11111111111111111111111111110111
-8 Complement ：11111111111111111111111111111000

         * [+3] = [00000000 00000000 00000000 000000011] primary 
         *      = [00000000 00000000 00000000 000000011] back 
         *      = [00000000 00000000 00000000 000000011] repair 
         * [-3] = [10000000 00000000 00000000 000000011] primary 
         *      = [11111111 11111111 11111111 111111100] back 
         *      = [11111111 11111111 11111111 111111101] repair

 Source code 、 Inverse code 、 Complement code 、 An operation （ And Application ）
  Subtracting a positive number from the algorithm is equal to adding a negative number ,  namely : 1-1 = 1 + (-1) = 0 ,  So machines can only add without subtraction ,  In this way, the design of computer operation is simpler .
         *
         *  So people began to explore   Take the sign bits in the operation ,  And just keep the method of addition .  First of all, let's look at the original code :
         *
         *  Calculate the decimal expression : 1-1=0
         *
         *  In order to solve the problem of subtraction of original code ,  There's an irony :
         *
         *     1 - 1 = 1 + (-1) = [0000 0001] primary  + [1000 0001] primary = [0000 0001] back  + [1111 1110] back  = [1111 1111] back  = [1000 0000] primary  = -0
         *
         *  We find that the subtraction is calculated by inverse code ,  The truth part of the result is right .  The only problem is that "0" On this particular value .  Although people understand +0 and -0 It's the same ,
         *          however 0 There's no point in having symbols .  And there will be [0000 0000] Original sum [1000 0000] The original two codes represent 0.
         *
         *  So the emergence of complement ,  It's solved 0 And two coding problems :
         *
         *     8 position ：1-1 = 1 + (-1) = [0000 0001] primary  + [1000 0001] primary 
         *                        = [0000 0001] repair  + [1111 1111] repair  //  Sign bits are also involved in the calculation of 
         *                        = [0000 0000] repair   
         *                          =[0000 0000] primary 
         *
         *  such 0 use [0000 0000] Express ,  And what happened before -0 There is no . And you can use [1000 0000] Express -128:
         *
     * (-1) + (-127) = [1000 0001] primary  + [1111 1111] primary  = [1111 1111] repair  + [1000 0001] repair  = [1000 0000] repair 
         *
         * -1-127 The result should be -128,  In the result of complement operation , [1000 0000] repair   Namely -128.  But notice because it's actually using the old -0 The complement of -128,
         *       therefore -128 There is no original code and no inverse code .( Yes -128 The complement of means [1000 0000] The original code to be calculated is [0000 0000] primary ,  This is not true )
         *
         *  Use complement ,  It's not just fixed 0 There are two coding problems ,  It can also represent a minimum number .  That's why 8 Bit binary ,
         *       The range represented by the original code or the inverse code is [-127, +127],  And the range represented by complement is [-128, 127].
         *
         *  Because the machine uses complement ,  So for the programming commonly used in 32 position int type ,  The range can be expressed as : [-231, 231-1]  Because the first bit represents the sign bit .
         *       When using the complement representation, you can save another minimum value .
 
         *      First int Most of the current computers are 32 position , Here we are for simplicity , Just as 8 Bit to handle （ Note that the highest bit is the sign bit , That is to say 8 The data representation range of bits is ：-128~127）,
         *      You only need to meet a few digits larger than it . Because computers are calculated by complement , The final result of the calculation is also the complement , The computer saves... In complement . However, it has to be transformed into 
         *      Original code （ Original code -> Inverse code -> Complement code -> Inverse code -> Original code ）. therefore 8 position 、6 position 、10 position 、32 position ....  It should be possible .
         *       8 position ： 1-1  See above 
         *       12 position ：1-1 = 1 + (-1) = [0000 0000 0001] primary  + [1000 0000 0001] primary 
         *                           = [0000 0000 0001] repair  + [1111 1111 1111] repair  //  Sign bits are also involved in the calculation of 
         *                           = [0000 0000 0000] repair  
         *                           = [0000 0000 0000] primary 
         *       32 position ： The calculation is the same 
         */
        /**
         *  Take the opposite ~ Operator   And   Inverse code is a different concept .
         *       Take the opposite ： Reverse all bits of complement , Get the result complement （ Computer storage ）, Finally, the original code is converted to the user .
         *       Inverse code ：1.  The high bit of the original code remains unchanged , Reverse other bits 
         *           2.  Complement to inverse , Complement code -1 It's the inverse code .
         *
         *  Computer calculations are based on complement , Storage is also the result of complement . If you show it to the user, you have to convert it into the original code .
         *          Complement to original ： The high complement is 0  Then complement = Inverse code = Original code 
         *                   The high complement is 1  Then the reverse code = Complement code -1, Original code = In addition to the high bit, the inverse code , All negative 
         *  1     ->    2      ->      3      ->     4     ->       5
         *  expression         Complement expression        result （ Complement code ）       Inverse code              Original code           Original code （10）
         * 1 & 3       0001 & 0011    0001( High position 0 just )  0001           0001           1
         * 1 & -3      0001 & 1101    0001( High position 0 just )  0001           0001           1
         * 1 ^ 3       0001 ^ 0011    0010( High position 0 just )  0010           0010           2
         * 1 | 3       0001 | 0011    0011( High position 0 just )  0011           0011           3
         * ~1    0001 First, reverse by bit to get the complement    1110( High position 1 negative )  1101           1010           -2
         *  For the calculation results （ Complement code ）, If it's a positive number , Just calculate to the second step . Because positive numbers   Original code == Inverse code == Complement code 
         *                   If it's negative , Then it needs to be calculated to the 4 Step .
         *

In this case 1 and -1 As shown in the following table ：

Common bit operations and skills - Simple books

<< >>

Shift operation ： Logical operations Arithmetic operations

Logical shift ： The removed bits are discarded , To use in a vacancy "0" fill .
Arithmetic shift ： The removed bits are discarded , To use in a vacancy " Sign bit " Fill in

Move left ： take a The whole binary of moves to the left N position , beyond 32 Give up a bit , The right side is not enough 0 To add .

int A = 12
int C = A << B    // C = A * 2^B（ If it doesn't overflow ）

eg： overflow 
INT_MAX              // 01111111 11111111 11111111 11111111( Complement code ) = 2147483647
INT_MAX << 1         // 11111111 11111111 11111111 11111110( Complement code ) = -2  ( Logical shift )

UINT_MAX             // 11111111 11111111 11111111 11111111 = 4294967295
UINT_MAX << 1        // 11111111 11111111 11111111 11111110 = 4294967294  ( Logical shift )

Move right

C++ Inside , Shift right operation is related to data type , Unsigned numbers are logical shifts , Signed numbers are arithmetic shifts .

https://leetcode-cn.com/problems/subsets/submissions/https://leetcode-cn.com/problems/subsets/submissions/https://leetcode-cn.com/problems/number-of-1-bits/submissions/

eg: No addition, subtraction, multiplication and division operators are needed to calculate a = b * 9( Don't think about spillovers )

// 1  analysis ： a=b*9=b*8+b
            8=<<3
            =b<<3   +b
// 2   test ： a=4*9=4<<3+4=32+4=36
             a=4*6=4<<2+4+4=24

int plusWithBit(int num1, int num2) {
    int xor_result = 0;
    int and_result = 0;

    while (num2) {
        xor_result = num1 ^ num2; // Different for 1  , Same as 0;
        and_result = num1 & num2;  // 1 1 1 Otherwise 0 

        num1 = xor_result;
        num2 = and_result << 1;
    }

    return xor_result;
}

int getNumber(int num1) {
    return  plusWithBit(num1 << 3, num1);
}

int A = 12
int C = A << B    // C = A / 2^B

eg：
INT_MIN              // 10000000 00000000 00000000 00000001( Complement code ) = -2147483648
INT_MIN >> 1         // 11000000 00000000 00000000 00000000( Complement code ) = -1073741824  ( Arithmetic shift )

UINT_MAX             // 11111111 11111111 11111111 11111111 = 4294967295
UINT_MAX >> 1        // 01111111 11111111 11111111 11111111 = 2147483647  ( Logical shift )

& All for 1 It's just 1,1 1 =1

    0 0 1 0 1 0
&   1 0 1 1 0 0
-------------------
    0 0 1 0 0 0

lowbit Method

11000 ===24

The lowest 1 1000=8;

n -n Everyone is against Add 1 ,24 -24

 10：01010 ( Complement code , The highest bit is the sign bit )
-10：10101( Inverse code , The inverse of a positive number is the original code , The inverse of a negative number is a sign bit invariant , The rest of the bits are reversed )
-10：10110（ Complement code , The complement of a positive number is the original code , The complement of a negative number is the inverse +1）

n &= -n;  // n The last one in the is 1 The position of is 1, The rest are 0

   0 1 0 1 0
&  1 0 1 1 0
----------------
   0 0 0 1 0

11000 & 01000==1

n&（-n）=lowbit; n-lowbit Remove one 1 n==0 Stop when

| As long as there is 1 Namely 1

    0 0 1 0 1 0
|   1 0 1 1 0 0
-------------------
    1 0 1 1 1 0

eg： Eliminate the rightmost one in the binary 1

// Binary data 
x=1100;
x-1=1011;
x&(x-1)=1000;  // & ==1 1 1 

bool cutRithtof1(int n) 
{
    return n > 0 && (n & (n-1)) == 0;
}

~ a Bitwise non 1 0 swap

    0 0 1 0 1 0
~  
-------------------
    0 1 0 1 0 1

^ Exclusive or - The most investigated

Different for 1 Otherwise 0;

    0 0 1 0 1 0
^   1 0 1 1 0 0
-------------------
    1 0 0 1 1 0

Exclusive or operation ：x ^ 0 = x , x ^ 1 = ~x
And operation ：x & 0 = 0 , x & 1 = x
a ^ b ^ b = a
b ^ b = 0
Use XOR exchange without extra space 2 Elements
The quality of XOR operation ：
If a ^ b = c, that a ^ c = b And b ^ c = a Simultaneous establishment , Use this , So exchange 2 There are the following methods for the value of variables ：
a = a ^ b
b = a ^ b
a = a ^ b
a = a + b    // new_a = old_a + old_b
b = a - b    // new_b = new_a - old_b = old_a + old_b - old_b = old_a
a = a - b    // new_a = new_a - new_b = old_a + old_b - old_a

eg 1

 Write a function , Input is an unsigned integer （ In the form of a binary string ）, Returns the number of digits in its binary expression as  '1'  The number of （ Also known as Han Ming weight ）.
 Input ：00000000000000000000000000001011
 Output ：3
 explain ： Binary string of input  00000000000000000000000000001011  in , There are three of them  '1'.
 Example  2：

 Input ：00000000000000000000000010000000
 Output ：1
 explain ： Binary string of input  00000000000000000000000010000000  in , There is one in all for  '1'.

 int hammingWeight(uint32_t n) 
    {
        int  cnt=0;

        for(int  i=0;i<32;i++ )
        {
           if((n>>i)&1)  //  Extract the most status 
           {
            cnt++;
           }
        }  //  The degree of time replication is  32
      //  return  cnt;
           // lowbit 
        int  count=0;

          while(n){
            int  lowbit=n&(-n);
            count++;
            n-=lowbit;
          } //  The degree of time replication is  O（logn）

     //  return  count;

      while (n != 0) 
      {
        n = n & (n - 1);
        count++;
       }
      return count;
    }

eg2： Power button

 Give you an array of integers  nums , Except that one element only appears   once   Outside , Every other element just happens to appear   Three times  . Please find and return the element that only appears once .

 

 Example  1：

 Input ：nums = [2,2,3,2]
 Output ：3



  
 int singleNumber(vector<int>& nums) 
    {
      //  The first method    Hash 
    //   unordered_map<int,int> map;
    //   for(int n:nums) map[n]++;
    //   for(const  auto& [num,count]:map)
    //   {
    //     if(count==1) return num;
    //   }
    //  return -1;
  

     //  second   in     An operation 
      int ones = 0, twos = 0;
        for(int num : nums){
            ones = ones ^ num & ~twos;
            twos = twos ^ num & ~ones;
        }
        return ones;
  
    }

eg3

 Array   Only one number appears once , The others appeared twice , Find this number 
   vector<int>  ans;
        unordered_map<int, int> freq;
        for (int num: nums)
         {
            ++freq[num];
        }
       
        for (const auto& [num, occ]: freq) {
            if (occ == 1) {
                ans.push_back(num);
            }
        }
        return ans;

 Give you an array of integers  nums , Except that one element only appears   once   Outside , Every other element just happens to appear   Three times  . Please find and return the element that only appears once .
      unordered_map<int,int> map;
      for(int n:nums) map[n]++;
      for(const  auto& [num,count]:map)
      {
        if(count==1) return num;
      }
      return -1;

eg; Power button https://leetcode-cn.com/problems/count-triplets-that-can-form-two-arrays-of-equal-xor/

eg5 ： Power button https://leetcode-cn.com/problems/number-complement/submissions/

eg： Power button https://leetcode-cn.com/problems/single-number/ Power button https://leetcode-cn.com/problems/bitwise-and-of-numbers-range/

    int rangeBitwiseAnd(int left, int right) 
    {
      int  ret=0;
     for(int i=30;i>=0;i--)
     {
       int  bl=(left>>i)&1;
       int  br=(right>>i)&1;
       if(bl&&br) //  The number of digits obtained is 1 
       {
         ret+=(1<<i);
       }else if(!bl&&br)
       {
         break;
       }
     } 
     return  ret;
    }

eg: Give you an array of integers nums , Except that one element only appears once Outside , Every other element just happens to appear Three times . Please find and return the element that only appears once . Power button https://leetcode-cn.com/problems/single-number-ii/


//  The idea of using numbers ,  By bit    Calculation 
    int singleNumber(vector<int>& nums)
     {
       int ret =0;
       // Process by bit 
       for(int  i=0;i<32;i++)
       {
         //  Count this one  0,1  The number of （0  In fact, the quantity of can be different ）
         int  cnt=0;
         for(int x:nums){
           int  b=(x>>i)&1;// Take it as a place  
           cnt +=b;
         }
         if(cnt%3)
         {
           ret+=(1<<i);
         }
       }
      return  ret;
    }

eg： Given an array of integers nums, There are exactly two elements that only appear once , All the other elements appear twice . Find the two elements that only appear once . You can press In any order Return to the answer . Power button https://leetcode-cn.com/problems/single-number-iii/

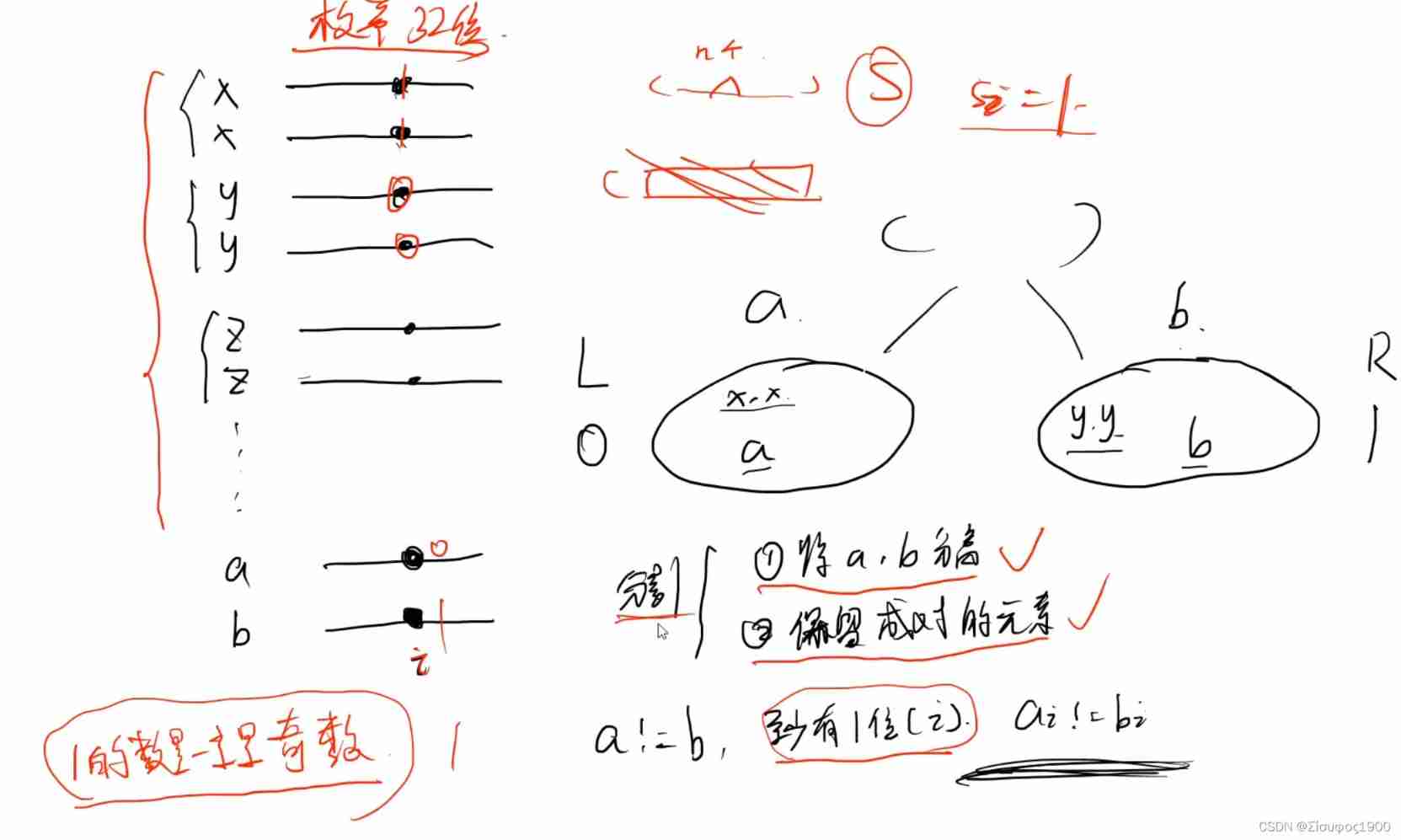
 vector<int> singleNumber(vector<int>& nums) 
    {
        // 1   The first 1 Kind of   Method 
        // vector<int>  res;
        // unordered_map<int, int> freq;
        // for (int num: nums)
        //  {
        //     ++freq[num];
        // }
       
        // for (const auto& [num, occ]: freq) {
        //     if (occ == 1) {
        //         res.push_back(num);
        //     }
        // }
        // return res;
       //




//   The second method  
       // 1  take a  b  Separate from  , Second, the same data must be put into the same group 
       vector<int> res;
       //  enumeration 32 position    find 1  The number of 
       int  s =0;//  XOR result of all elements 
       for(int n:nums)
       {
          s^=n;
       }

       // s   i =  1    In the original sequence , Give a seat yes   An odd number 1 
       int  pos=-1;
       for(int  i=0;i<32;i++)
       {
           if((s>>i)&1)  // Get is 1 
           {
               pos=i;
               break;
           }
       }

       //  grouping   
       int x=0;
       int y=0;
       for(int n:nums)
       {
           int  m=(n>>pos)&1;
           if(!m){
               x^=n;
           }else{
              y^=n;
           }
       }

       return {x,y};

    }

eg Give you an array of integers nums , return nums[i] XOR nums[j] The largest operation result of , among 0 ≤ i ≤ j < n .

Power button

class Solution {
public:

//   Dictionary tree 
    typedef  struct  Node
    {
      int  son[2];
      Node(){
        son[0]=-1;
        son[1]=-1;
      }
    }Node;
     // int  b2=1^b   ====1-b;
    vector<Node>   nodes;

    void insert(int x)
    {
        int  id=0;
        for(int i=31;i>=0;i--)
        {
             int  b=(x>>i)&1;
             if(nodes[id].son[b]==-1)
             {
               nodes.push_back({});
               nodes[id].son[b] = nodes.size()-1;
             }
             id=nodes[id].son[b];
        }
    }

    int  query(int x)
    {
      int  ret=0;
      int  id=0;
       for(int i=31;i>=0;i--)
        {
             int  b=(x>>i)&1;
             int   b2=1^b;// 1-b

             if(nodes[id].son[b2]!=-1){
               id=nodes[id].son[b2];
               ret+=(1<<i);
             }else{
               id=nodes[id].son[b];
             }

       }

       return  ret;

    }

    int findMaximumXOR(vector<int>& nums) 
    {
         //  From high position to position 
         if(nums.empty())  return 0;


     nodes.push_back({});

     insert(nums.back());
     int ret=0;
     for(int  i=nums.size()-2;i>=0;i--){
         int  ans=query(nums[i]);
         ret =max(ret,ans);
         insert(nums[i]);
     }

      return  ret;
    }
};

skill 4： Of the circular queue buffer size Why do we need to guarantee 2 The power of ？

Why do you need to guarantee buffer size by 2 The power of ？

Because usually the incoming and outgoing operations of the circular queue need to be constantly correct size Make a balance , In order to improve efficiency , take buffer size Expand to 2 The power of , You can use bit operations .kfifo->in % kfiifo->size Equate to kfifo->in & (kfifo->size – 1).

Suppose now size by 16：
8 & (size - 1) = 01000 & 01111 = 01000 = 8
15 & (size -1) = 01111 & 01111 = 01111 = 15
16 & (size - 1) = 10000 & 01111 = 00000 = 0
26 & (size - 1 ) = 11010 & 01111 = 01010 = 10

So promise size yes 2 Under the premise of the power of , The remainder can be obtained by bit operation , In the case of frequent operation on columns, it can greatly improve the efficiency .

原网站

版权声明
本文为[Σίσυφος one thousand and nine hundred]所创，转载请带上原文链接，感谢
https://yzsam.com/2022/02/202202150539425701.html