当前位置:网站首页>【多任务优化】DWA、DTP、Gradnorm(CVPR 2019、ECCV 2018、 ICML 2018)
【多任务优化】DWA、DTP、Gradnorm(CVPR 2019、ECCV 2018、 ICML 2018)
2022-08-01 19:53:00 【chad_lee】
多任务学习模型的优化
有多个task就有多个loss,常见的MTL模型loss可以直接简单的对多个任务的loss相加:
L = ∑ i L i L=\sum_{i} L_{i} L=i∑Li
显然这种做法有很大问题,因为不同task的label分布不同,同时不同task的loss量级也不同,整个模型很可能被一些loss特别大的任务主导。最简单的方法是加权loss,人工设计权重:
L = ∑ i w i ∗ L i L=\sum_{i} w_{i} * L_{i} L=i∑wi∗Li
但是这样这个权重在整个训练周期中都是固定的,不同训练阶段权重可能变化,动态权重则为:
L = ∑ i w i ( t , θ ) ∗ L i L=\sum_{i} w_{i}(t, \theta) * L_{i} L=i∑wi(t,θ)∗Li
t是训练的step,theta是模型其他参数。但是这种做法也不一定有人工设计权重好。
一些设计 w i ( t , θ ) w_{i}(t, \theta) wi(t,θ) 的方法:
《End-to-End Multi-Task Learning with Attention》 CVPR 2019
CVPR 2019的《End-to-End Multi-Task Learning with Attention》提出的Dynamic Weight Averaging(DWA),核心公式如下所示:
r n ( t − 1 ) = L n ( t − 1 ) L n ( t − 2 ) w i ( t ) = N exp ( r i ( t − 1 ) / T ) ∑ n exp ( r n ( t − 1 ) / T ) \begin{gathered} r_{n}(t-1)=\frac{L_{n}(t-1)}{L_{n}(t-2)} \\ w_{i}(t)=\frac{N \exp \left(r_{i}(t-1) / T\right)}{\sum_{n} \exp \left(r_{n}(t-1) / T\right)} \end{gathered} rn(t−1)=Ln(t−2)Ln(t−1)wi(t)=∑nexp(rn(t−1)/T)Nexp(ri(t−1)/T)
$L_{n}(t-1) 是任务 n 在 t − 1 时的训练 l o s s ,因此 是任务 n 在 t-1 时的训练loss,因此 是任务n在t−1时的训练loss,因此r_{n}(t-1) $ 是此时loss的下降速度,$r_{n}(t-1) $越小,训练速度越快。(已经开始收敛,loss=0时结束了)
w i ( t ) w_i(t) wi(t)代表不同任务loss的权重,直观理解就是loss收敛越快的任务,权重越小,权重的平均程度由温度系数T控制
《Dynamic task prioritization for multitask learning》 ECCV 2018
DTP(Dynamic Task Prioritization):
w i ( t ) = − ( 1 − k i ( t ) ) γ i log ( k i ( t ) ) w_{i}(t)=-\left(1-k_{i}(t)\right)^{\gamma_{i}} \log \left(k_{i}(t)\right) wi(t)=−(1−ki(t))γilog(ki(t))
$k_i(t) $ 表示第t步的某衡量kpi值,取值维0~1之间,比如在分类任务中KPI可以是训练集上的准确率等,可以反应模型在这个任务上的拟合程度,γ是人工调节的温度系数。直观理解就类似focal loss,优化的越好的任务,获得的权重越小。
《Gradnorm: Gradient normalization for adaptive loss balancing in deep multitask networks》 ICML 2018
影响力最大的是GradNorm。其核心思想相对前述的DWA和DTP更为复杂,核心观点为
不仅考虑loss收敛的速度,进一步希望loss本身的量级能尽量接近
不同的任务以相近的速度训练(与gradient相关)
从带参数的动态权重 $L=\sum_{i} w_{i}(t, \theta) * L_{i} $出发,作者还定义了一个训练权重 $w_i(t,\theta) $ 相关的 gradient loss。(定一个loss用来优化训练loss的权重)
w i ( t ) w_i(t) wi(t) 刚开始初始化为1 或者超参,然后用gradient loss来优化。
首先得到任务 i 在 t 时刻的 梯度的2范数,以及所有任务的平均值:
G W ( i ) ( t ) = ∥ ∇ W ( w i ( t ) L i ( t ) ) ∥ 2 G ˉ W ( t ) = A V G ( G W ( i ) ( t ) ) \begin{gathered} G_{W}^{(i)}(t)=\left\|\nabla_{W}\left(w_{i}(t) L_{i}(t)\right)\right\|_{2} \\ \bar{G}_{W}(t)=A V G\left(G_{W}^{(i)}(t)\right) \end{gathered} GW(i)(t)=∥∇W(wi(t)Li(t))∥2GˉW(t)=AVG(GW(i)(t))
其中W是模型参数的子集,也是需要应用Gradient Normalization的参数集,一般是选择模型中共享参数的最后一层。然后得到不同任务loss的训练速度:
L ~ i ( t ) = L i ( t ) / L i ( 0 ) r i ( t ) = L ~ i ( t ) / A V G ( L ~ i ( t ) ) \begin{gathered} \tilde{L}_{i}(t)=L_{i}(t) / L_{i}(0) \\ r_{i}(t)=\tilde{L}_{i}(t) / A V G\left(\tilde{L}_{i}(t)\right) \end{gathered} L~i(t)=Li(t)/Li(0)ri(t)=L~i(t)/AVG(L~i(t))
$r_{i}(t) $衡量任务训练的速度, $r_{i}(t) $ 越大,表明任务训练的越慢。这点和DWA的思想接近,但是这里使用的是第一步的loss,而不是DWA中的前一步loss。
最终gradient loss为:
L g r a d ( t ; w i ( t ) ) = ∑ i ∣ G W ( i ) ( t ) − G ˉ W ( t ) ∗ [ r i ( t ) ] α ∣ 1 L_{g r a d}\left(t ; w_{i}(t)\right)=\sum_{i}\left|G_{W}^{(i)}(t)-\bar{G}_{W}(t) *\left[r_{i}(t)\right]^{\alpha}\right|_{1} Lgrad(t;wi(t))=i∑∣∣GW(i)(t)−GˉW(t)∗[ri(t)]α∣∣1
- $\bar{G}{W}(t) *\left[r{i}(t)\right]^{\alpha} $表示理想的梯度标准化后的值。**这里的gradient loss只用于更新 $w_{i}(t) ∗ ∗ 。 **。 ∗∗。w_{i}(t) $还会经过最终的重normalize,使得 $\sum_{i} w_{i}(t)=N $,N是任务的数量。
- α是设定恢复力强度的超参数,即将任务的训练速度调节到平均水准的强度。如果任务的复杂程度很不一样,大致人物之间的学习速率大不相同,就应该使用较高的alpha来进行较强的训练速率平衡;反之对于多个相似的任务,应该使用较小的α。
- 从gradient loss的定义来看, $r_i(t) $ 越大,表明训练越快,gradient loss越大;$\left|G_{W}^{(i)}(t)-\bar{G}{W}(t)\right| 表明 l o s s 量级的变化,不论 表明loss量级的变化,不论 表明loss量级的变化,不论G{W}^{(i)}(t) $过大或者过小都会导致gradient loss变大。
- 所以gradient loss 希望:1、不同任务的loss的量级接近;2、不同任务以相近的速度训练(收敛速度)

边栏推荐
- 密码学的基础:X.690和对应的BER CER DER编码
- SQL的 ISNULL 函数
- GEE(8):使用MODIS填补由去云后的Landsat影像计算得到的NDVI数据
- 有序双向链表的实现。
- 洛谷 P2440 木材加工
- MLX90640 Infrared Thermal Imager Temperature Measurement Module Development Notes (Complete)
- JS数组过滤
- 57: Chapter 5: Develop admin management services: 10: Develop [get files from MongoDB's GridFS, interface]; (from GridFS, get the SOP of files) (Do not use MongoDB's service, you can exclude its autom
- What are the application advantages of SaaS management system?How to efficiently improve the digital and intelligent development level of food manufacturing industry?
- 第55章 业务逻辑之订单、支付实体定义
猜你喜欢
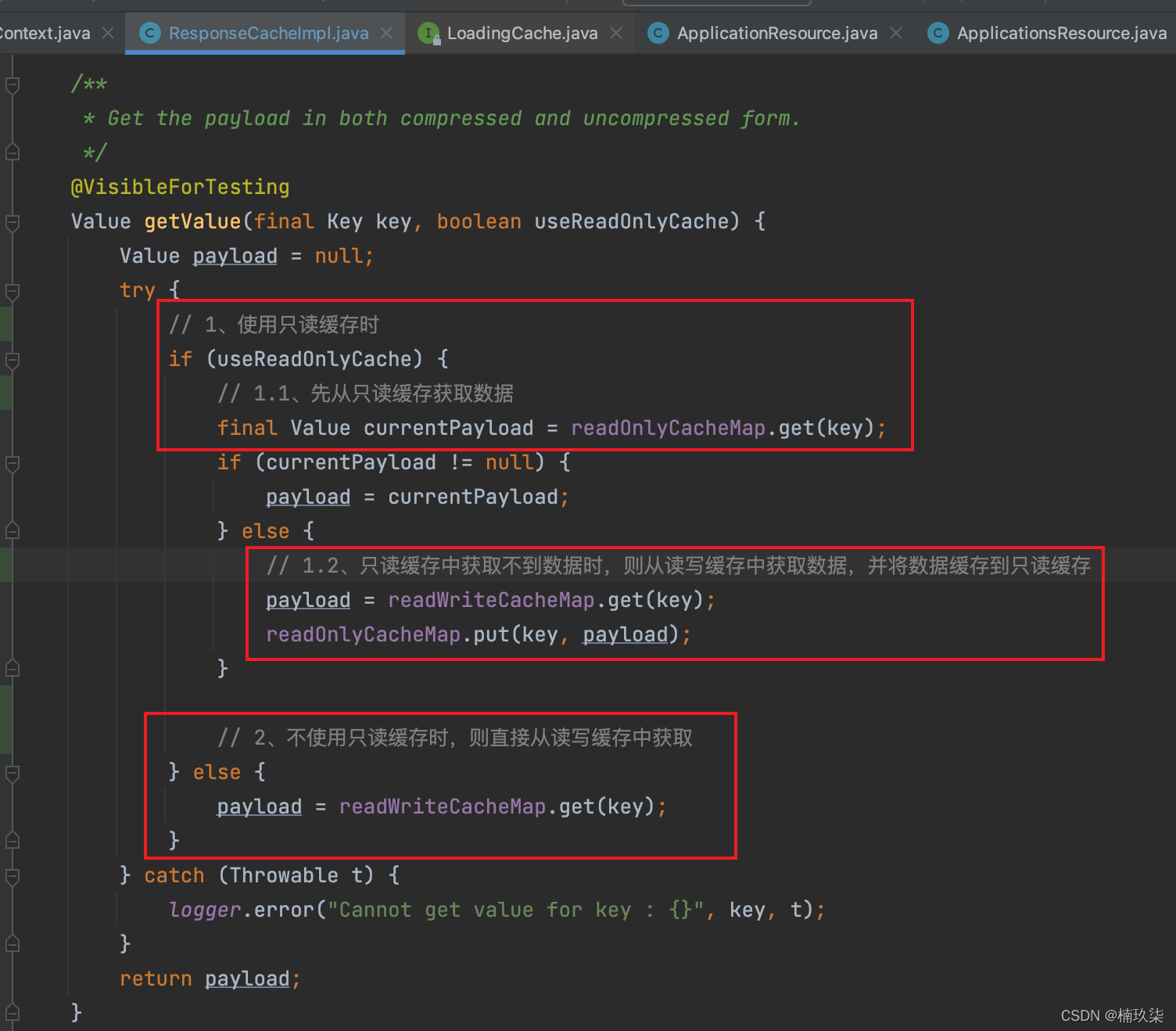
The graphic details Eureka's caching mechanism/level 3 cache

正则表达式

为什么限制了Oracle的SGA和PGA,OS仍然会用到SWAP?

MySQL你到底都加了什么锁?
What should I do if the Win11 campus network cannot be connected?Win11 can't connect to campus network solution

因斯布鲁克大学团队量子计算硬件突破了二进制

我的驾照考试笔记(1)
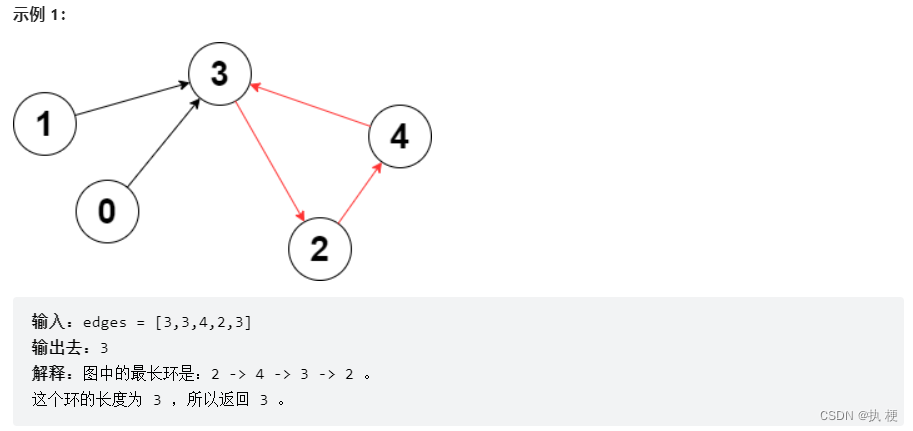
【周赛复盘】LeetCode第304场单周赛

小白系统初始化配置资源失败怎么办

Ha ha!A print function, quite good at playing!
随机推荐
The solution to the vtk volume rendering code error (the code can run in vtk7, 8, 9), and the VTK dataset website
不恰当Equatable协议==方法的实现对SwiftUI中@State修饰属性的影响
Pytorch模型训练实用教程学习笔记:四、优化器与学习率调整
Arthas 常用命令
大整数相加,相减,相乘,大整数与普通整数的相乘,相除
数据库系统原理与应用教程(072)—— MySQL 练习题:操作题 121-130(十六):综合练习
LabVIEW 使用VISA Close真的关闭COM口了吗
油猴hook小脚本
[Server data recovery] Data recovery case of offline multiple disks in mdisk group of server Raid5 array
八百客、销售易、纷享销客各行其道
第60章 ApplicationPart自动集成整体性和独立性插件项
【Redis】缓存雪崩、缓存穿透、缓存预热、缓存更新、缓存击穿、缓存降级
Try compiling QT test on Allwinner V853 development board
【kali-信息收集】(1.2)SNMP枚举:Snmpwalk、Snmpcheck;SMTP枚举:smtp-user-enum
使用常见问题解答软件的好处有哪些?
1个小时!从零制作一个! AI图片识别WEB应用!
XSS靶场中级绕过
From ordinary advanced to excellent test/development programmer, all the way through
Choosing the right DevOps tool starts with understanding DevOps
C语言实现-直接插入排序(带图详解)