当前位置:网站首页>LeetCode 497. 非重叠矩形中的随机点(前缀和+二分)
LeetCode 497. 非重叠矩形中的随机点(前缀和+二分)
2022-06-12 11:46:00 【xylitolz】
题目



解法:前缀和+二分
整体思路:先随机确定在哪个矩形内取点,再在该矩形内随机取点。
对于第二步,根据矩形特质,只需在该矩形的 XY 坐标范围内随机即可确保等概率
对于第一步(随机确定矩形)为了确保是等概率,需要结合每个矩形覆盖的点数来做。
矩形 rects [ i ] \textit{rects}[i] rects[i] 的左下角点为 ( a i , b i ) (a_i, b_i) (ai,bi), 右上角点为 ( x i , y i ) (x_i, y_i) (xi,yi),则它覆盖的整数点有 s i = ( x i − a i + 1 ) × ( y i − b i + 1 ) s_i = (x_i-a_i+1)\times(y_i-b_i+1) si=(xi−ai+1)×(yi−bi+1)个。
将 rects [ 0 ] \textit{rects}[0] rects[0] 覆盖的点编号为 1 至 s 0 s_0 s0, rects [ 1 ] \textit{rects}[1] rects[1] 覆盖的整数点有 s 1 s_1 s1个,编号为 s 0 + 1 s_0 + 1 s0+1 至 s 0 + s 1 s_0+s_1 s0+s1,依此类推。
预处理一个前缀和数组 arr(前缀和数组下标默认从 1 开始),其中 arr[i] 代表前 i 个矩形的覆盖的点数之和(即下标范围 [0, i - 1] 的点数总和),最终 arr[n] 为所有矩形的覆盖的总点数,可以在 [1, arr[n]] 范围内随机,假定随机到的值为 k,然后利用 arr 数组的具有单调性,进行「二分」,找到 k 所在的矩形,然后在该矩形中进行随机,得到最终的随机点。
class Solution {
Random rand;
int[][] rects;
// arr[0] = 0;
// arr[1] = n; 第一个矩形有n个点
// arr[2] = m + n; 第二个矩形有m个点
List<Integer> arr; // 前缀和数组
int num; // 一共有 num - 1 个矩形
public Solution(int[][] rects) {
rand = new Random();
this.rects = rects;
arr = new ArrayList<>();
arr.add(0);
// 构造前缀和数组
for (int[] r : rects) {
int a = r[0], b = r[1], x = r[2], y = r[3];
// 前面矩形覆盖的总点数
int n = arr.get(arr.size() - 1);
// 当前矩形覆盖的点数
int m = (x - a + 1) * (y - b + 1);
arr.add(n + m);
}
num = arr.size();
}
public int[] pick() {
// 1. 确定在哪个矩形内取点
// 获取[0, rects覆盖的总点数 - 1]之间的一个随机数
int k = rand.nextInt(arr.get(num - 1));
// 利用二分确定该点属于第几个矩形(对应到rects的索引应该减1)
// k + 1 是因为点的编号是从1开始的
int rectIndex = binarySearch(arr, k + 1);
// 2. 在rects[rectIndex - 1]对应的矩形内选点
int[] rect = rects[rectIndex - 1];
int x = rect[2] - rect[0] + 1;
int y = rect[3] - rect[1] + 1;
int a = rand.nextInt(x) + rect[0];
int b = rand.nextInt(y) + rect[1];
return new int[]{
a, b};
}
private int binarySearch(List<Integer> arr, int target) {
int left = 0, right = num;
while (left < right) {
int mid = left + (right - left) / 2;
if (arr.get(mid) < target) {
left = mid + 1;
} else {
right = mid;
}
}
return left;
}
}
/** * Your Solution object will be instantiated and called as such: * Solution obj = new Solution(rects); * int[] param_1 = obj.pick(); */
时间复杂度:构造函数复杂度为 O ( n ) O(n) O(n), pick \textit{pick} pick 函数复杂度为 O ( log n ) O(\log n) O(logn),其中 n n n 为 rects \textit{rects} rects 的长度。构造函数需要构造前缀和数组, pick \textit{pick} pick函数需要在前缀和数组内进行二分。
空间复杂度:构造函数复杂度为 O ( n ) O(n) O(n), pick \textit{pick} pick 函数复杂度为 O ( 1 ) O(1) O(1)。构造函数需要构造前缀和数组, pick \textit{pick} pick 函数只需要使用常数空间。
Reference
边栏推荐
猜你喜欢

Logrotate log rotation method create and copyruncate principles

manuscript手稿格式准备

Design of secure chat tool based on C #

MySQL45讲 01 | 基础架构:一条SQL查询语句是如何执行的?
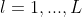
Inter class and intra class relations in video classification -- regularization

Node crawler puppeter usage

UML series articles (31) architecture modeling - deployment diagram

Manuscript manuscript format preparation

Index in MySQL show index from XXX the meaning of each parameter

6.6 RL:MDP及奖励函数
随机推荐
Windows10 install mysql-8.0.28-winx64
Les humains veulent de l'argent, du pouvoir, de la beauté, de l'immortalité, du bonheur... Mais les tortues ne veulent être qu'une tortue.
C# 36. DataGridView line number
6.6 RL:MDP及奖励函数
Rich text editor copying pictures in word documents
Why is there no traffic after the launch of new products? How should new products be released?
TinyMCE realizes automatic uploading of pasted pictures
【藍橋杯單片機 國賽 第十一届】
Design of tablewithpage
ARM处理器模式与寄存器
UML series articles (30) architecture modeling -- product diagram
C# 37. textbox滚动条与多行
标品和非标品如何选品,选品的重要性,店铺怎样布局
MySQL45讲 01 | 基础架构:一条SQL查询语句是如何执行的?
【QNX Hypervisor 2.2 用户手册】4 构建QNX Hypervisor系统
如何确定首页和搜索之间的关系呢?首页与搜索的关系
Architecture training module 7
TinyMCE series (IV) introduction to common built-in UI components of TinyMCE
Lambda表达式 | 浅解
UML series articles (31) architecture modeling - deployment diagram