C语言进阶篇——浮点型在内存中的存储

大家好我是沐曦希

---

1.浮点型在内存中的存储

常见的浮点数：

3.14159
1E10//1*10^10（1*10的10次方）
浮点数家族包括：float(单精度浮点数）；double(双精度浮点数）;long double类型。
浮点数家族表示的范围：float.h中定义
整型家族表示的范围：limits.h中定义

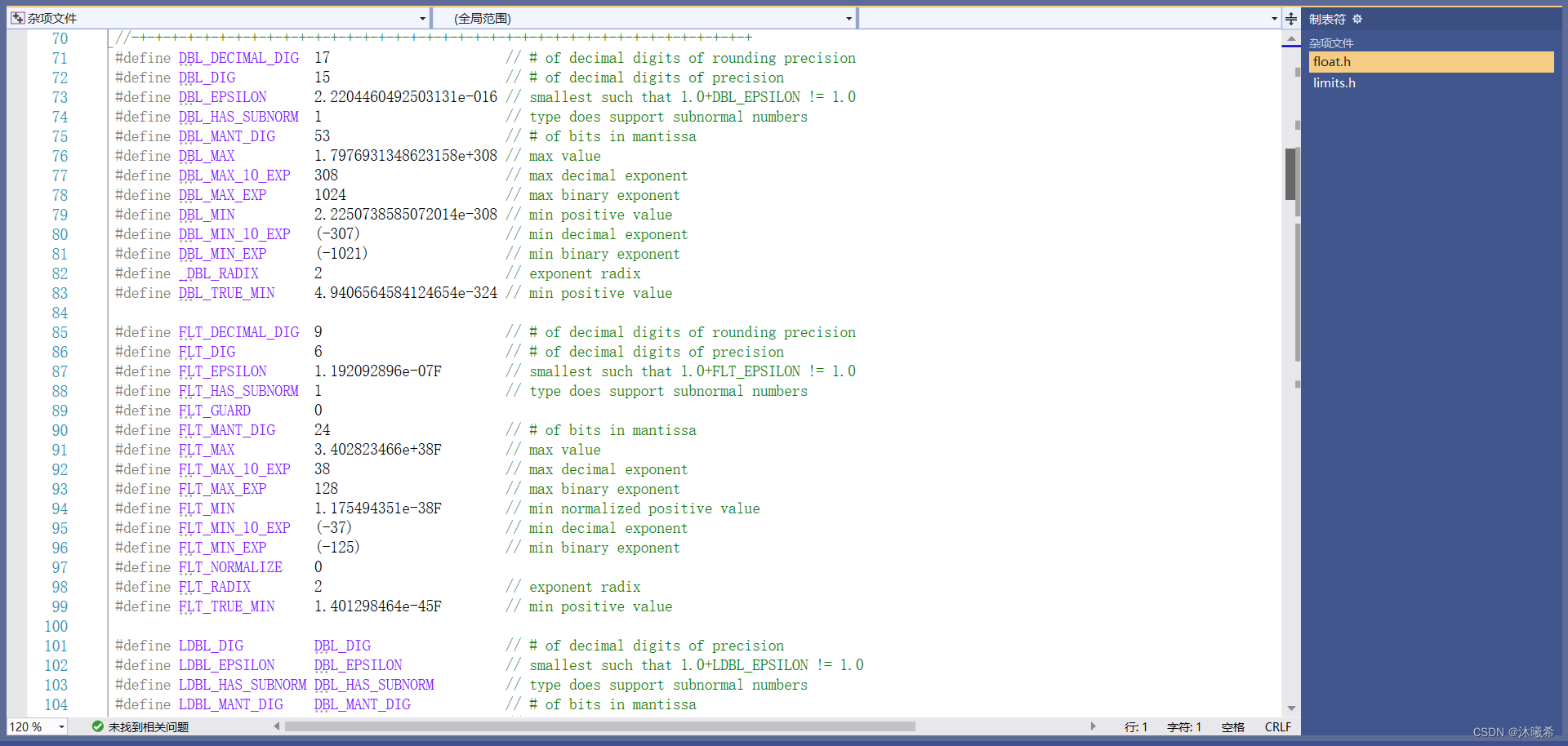
例子

浮点数存储的例子：

int main()
{
    
 int n = 9;
 float *pFloat = (float *)&n;
 printf("n的值为：%d\n",n);
 printf("*pFloat的值为：%f\n",*pFloat);
 *pFloat = 9.0;
 printf("num的值为：%d\n",n);
 printf("*pFloat的值为：%f\n",*pFloat);
 return 0;
}

输出的结果是什么呢？

由此可见整型的存储规则与浮点数存储的规则不一样。

浮点数存储规则

n 和 *pf 在内存中明明是同一个数，为什么浮点数和整数的解读结果会差别这么大？
要理解这个结果，一定要搞懂浮点数在计算机内部的表示方法。
根据国际标准IEEE（电气和电子工程协会） 754，任意一个二进制浮点数V可以表示成下面的形式：

(-1)^S * M * 2^E
(-1)^S表示符号位，当S=0，V为正数；当S=1，V为负数。
M表示有效数字，大于等于1，小于2。
2^E表示指数位。

例如：
十进制中的5.0转换成二进制是101.0，相当于1.01*2^2
(二进制中0.1表示1*2^(-1); 0.11表示1*2^(-1)+1*2^(-2))
那么，按照上面V的格式，可以得出S=0，M=1.01，E=2。
十进制的-5.0，写成二进制是 -101.0 ，相当于 -1.01×2^2 。那么，S=1，M=1.01，E=2。
V=9.5f=1001.1=(-1)^0*1.0011*2^3
相当于S=0；M=1.0011；E=3。

IEEE 754规定

对于32位的浮点数，最高的1位是符号位s，接着的8位是指数E，剩下的23位为有效数字M。
单精度浮点数存储模型：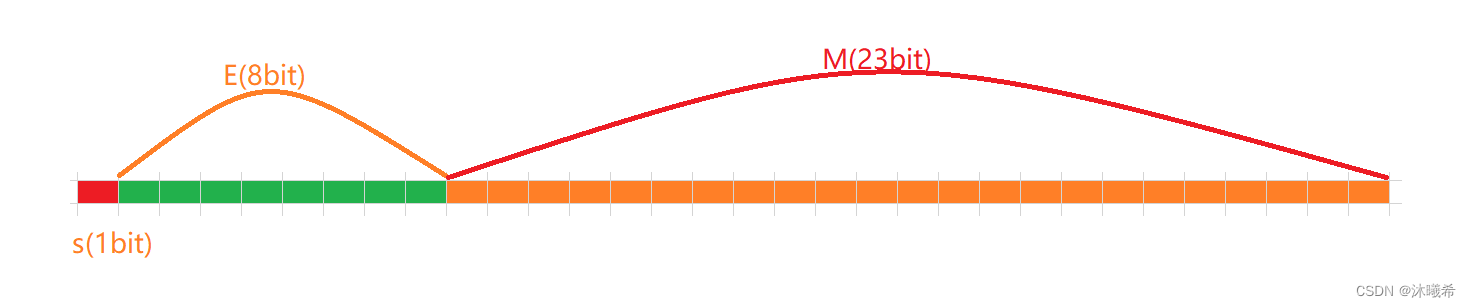

对于64位的浮点数，最高的1位是符号位S，接着的11位是指数E，剩下的52位为有效数字M。
双精度浮点数存储模型：

IEEE 754对有效数字M和指数E，还有一些特别规定。
前面说过， 1≤M<2 ，即M可以写成 1.xxxxxx 的形式，其中xxxxxx表示小数部分。

IEEE 754规定，在计算机内部保存M时，默认这个数的第一位总是1，因此可以被舍去，只保存后面的xxxxxx部分。比如保存1.01的时候，只保存01，等到读取的时候，再把第一位的1加上去。这样做的目的，是节省1位有效数字。以32位浮点数为例，留给M只有23位，将第一位的1舍去以后，等于可以保存24位有效数字。

对于指数E的规定更为复杂。

指数E

E为一个无符号整数

这意味着，如果E为8位，它的取值范围为0_{255；如果E为11位，它的取值范围为0}2047。但是，我们知道，科学计数法中的E是可以出现负数的，所以IEEE 754规定，存入内存时E的真实值必须再加上一个中间数，对于8位的E，这个中间数是127；对于11位的E，这个中间数是1023。比如，2^10的E是10，所以保存成32位浮点数时，必须保存成10+127=137，即1000 1001。保存成64位浮点数时，必须保存成10+1023=1024，即100 0000 1001。
例如：
V=0.5f；
\\（-1）^0*1.0*2^(-1)
保存成32位浮点数时，必须保存成E+127–>126
保存成64位浮点数时，必须保存成E+1023–>1022
即float–>E（真实值）+127（中间值）–>存储值
即double–>E（真实值）+1023（中间值）–>存储值
然后，指数E从内存中取出还可以再分成三种情况：

E不全为0或不全为1

这时，浮点数就采用下面的规则表示，即指数E的计算值减去127（或1023），得到真实值，再将有效数字M前加上第一位的1。 比如：
0.5（1/2）的二进制形式为0.1，由于规定正数部分必须为1，即将小数点右移1位，则为1.0*2^(-1)，其阶码为-1+127=126，表示为01111110，而尾数1.0去掉整数部分为0，补齐0到23位00000000000000000000000，则其二进制表示形式为:
0 01111110 00000000000000000000000

E全为0

当浮点数的指数E等于1-127（或者1-1023）即为真实值，
有效数字M不再加上第一位的1，而是还原为0.xxxxxx的小数。这样做是为了表示±0，以及接近于0的很小的数字。

E全为1

当有效数字M全为0，表示±无穷大（正负取决于符号位s）；

解释例子

第一部分，将 0x00000009 拆分，得到第一位符号位s=0，后面8位的指数 E=00000000 ，
最后23位的有效数字M=000 0000 0000 0000 0000 1001。

9 -> 0000 0000 0000 0000 0000 0000 0000 1001

由于指数E全为0，所以符合上一节的第二种情况。因此，浮点数V就写成：
　　 V=(-1)^0 * 0.00000000000000000001001*2^(-126)=1.001*2^(-146)
显然，V是一个很小的接近于0的正数，所以用十进制小数表示就是0.000000。
第二部分
首先，浮点数9.0等于二进制的1001.0，即1.001×2^3。

9.0 -> 1001.0 ->(-1)^01.0012^3 -> s=0, M=1.001,E=3+127=130

那么，第一位的符号位s=0，有效数字M等于001后面再加20个0，凑满23位，指数E等于3+127=130，即10000010。
所以，写成二进制形式，应该是s+E+M，即

0 10000010 001 0000 0000 0000 0000 0000

这个32位的二进制数，还原成十进制，正是 1091567616 。

4.写在最后

友友们觉得不错的可以给个关注，点赞或者收藏哦！感谢各位友友们的支持。

你的️点赞是我创作的动力的源泉
你的收藏是我奋斗的方向
你的关注是对我最大的支持
你的️评论是我前进的明灯
创作不易，希望大佬你支持一下小沐吧