当前位置:网站首页>损失函数(第五周)
损失函数(第五周)
2022-08-03 05:23:00 【白小李】
目录
前言
设计损失函数的三种方法
1、最小二乘法
2、极大似然估计法
3、交叉熵法
最小二乘法

x是经过人的认定后给图片打上的标签结果,x为0,则代表不是猫,为1则代表是猫
y则是图片经过神经网络后,由sigmoid函数输出的一个值,范围是0到1,即待变这个图片是猫的概率是多大。
w代表神经网络中感知机线性函数未知数的系数,b是代表线性函数的偏置系数。
在最后就是算x和y之间的差距,每一张图的差值都算出来,最后选取一个最小的,相当于神经网络中判断猫的模型和人脑中判断猫的模型最近似的结果。

上述的说法即是最小二乘法。
缺陷:当用它作为损失函数进行梯度下降的时候,会特别麻烦。
极大似然估计法
理念世界会指导显示世界。倘若硬币的概率分布按照正反都是0.5的方式进行,那抛硬币的结果就是正反0.5分布。
现实世界也能往理念世界进行反推,抛了10次硬币结果是正反各5个,即认定硬币遵守的概率分布就是正反0.5。
但理念世界和现实世界中间隔着一层次元壁。即抛10次硬币,正反不一定是0.5。
通过在现实世界的情况算出在理论世界中这种模型发生正或反情况的概率。


似然值是真实的情况已经发生,假设它有很多模型,在这个概率模型下,发现这种情况的可能性。
即从结果去反推产生这个结果的概率模型的时候往往会用到最大似然估计法。
极大似然估计本质上是计算神经网络里面的概率模型的似然值,找到极大似然值,这个就是最接近现实情况的那个概率模型。
同样是对神经网络输入猫的例子。

转换过来就是

最后得到的值就是似然值,当这个似然值最大的时候,则可以认定神经网络里的模型和人脑中的模型是最接近的。
总结
还剩一个交叉熵法没学,计划在下周对其进行学习。
边栏推荐
猜你喜欢
Sentinel初次使用Demo测试
Apache2-XXE vulnerability penetration
磁盘空间管理

下拉框数据字典应用案例
Execute the mysql script file in the docker mysql container and solve the garbled characters

让小程序开发进入 `tailwind jit` 时代

【解读合约审计】Harmony的跨链桥是如何被盗一亿美金的?
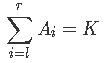
A-B数对问题|UPC-Count Interval|洛谷-P1102A-B数对
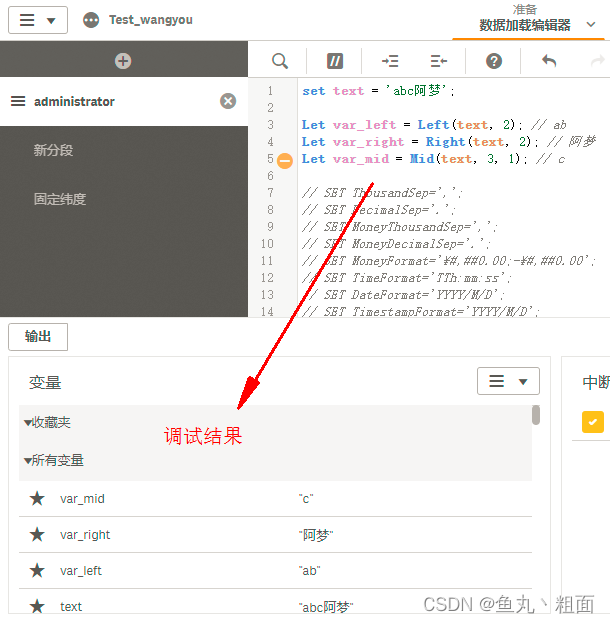
Qlik Sense 字符串截取和拼接详解(Left、Right、&)
对页码的使用总结
随机推荐
The result of request.getParameter is on
中国柔性制造系统(FMS)市场发展动态及未来趋势预测报告2022~2028年
request.getParameter的结果为on
Browser multi-threaded off-screen rendering, compression and packaging scheme
该描述怎么写成SQL语句
【 command execution and middleware loopholes 】
优雅的拦截TabLayout的点击事件
Sqli-labs-master shooting range 1-23 customs clearance detailed tutorial (basic)
Oracle count(1)、count(*)、count(列) 区别详解
C# Base64加密
pta a.1003 的收获
东南亚跨境电商
MySQL 安装报错的解决方法
【frp内网穿透】
中国石油行业并购重组趋势与投资战略规划建议报告2022~2028年
自定义封装组件-国际化-下拉搜索
中国生产力促进中心”十四五”规划与发展规模分析报告2022~2028年
opencv
Leetcode刷题——一些用层次遍历解决的问题(111. 二叉树的最小深度、104. 二叉树的最大深度、226. 翻转二叉树、剑指 Offer 27. 二叉树的镜像)
Django从入门到放弃三 -- cookie,session,cbv加装饰器,ajax,django中间件,redis缓存等