当前位置:网站首页>Combination series - there are combinations when there are arrangements
Combination series - there are combinations when there are arrangements
2022-07-31 14:07:00 【DiGeT】
The focus of the combined questions is the sequence problem,He's not like a permutation,Different orders represent a permutation,So combined traversal.Of course, the last question is a combination of the title itself,所以会有所不同.
77. 组合
选择1~n中的k个数,构造出所有组合,Each of these numbers cannot be reused(隐含条件)
思路:DFS,回溯
- 参数说明:
pre,Used to record the subscript of the previous number,Note that combination is not the same as arrangement,The combination doesn't matter the order,也就是12和21是一样的,So need to avoid repeated combinations.==The specific method is to ensure that the subscripts of the elements in the combination are in order,That is, the subscript of the currently traversed element is greater than the previous one,也就是pre<i.需要注意的是,这里的pre初始化是0,而不是-1,because the given element is 1-n,直接用1-nThe subscript corresponding to .layer,代表递归层数,Or the number of combinations,kRepresents a combination withk个数,当layer==k +1时,说明已经找到k个数,Save the combined result directly,No more recursion needed. - 剪枝条件:
k-layer > n-ik-layerThe representative combination is still a few numbers away,n-iIndicates how many numbers are left to choose.If the number of combinations required exceeds the selectable,Indicates that the number of choices is not enough,Unable to make a combination,直接return.例如12345,k=4,layer=1,i=4,If the first combination number selected is 3,还差3个,But only available4和5两个数,所以直接返回
No pruning,code is correct,Pruning is for efficiency,减少不必要的计算.
class Solution {
//Just record the combined result,你也可以用list集合代替
private boolean[] record;
//结果
private List<List<Integer>> res;
public List<List<Integer>> combine(int n, int k) {
record = new boolean[n + 1];
res = new ArrayList<>();
dfs(n, k, 0, 1);
return res;
}
public void dfs(int n, int k, int pre, int layer) {
//边界
if (layer == k + 1) {
//也可用List集合
Integer[] zuhe = new Integer[k];
int idx=0;
for (int i = 1; i <=n; i++) {
if (record[i]) {
zuhe[idx++] = i;
}
}
res.add(Arrays.asList(zuhe));
return;
}
//递归
for (int i = 1; i <= n; i++) {
//剪枝
if(k - layer > n - i) {
return;
}
if (pre < i) {
record[i] = true;
dfs(n, k, i, layer + 1);
record[i] = false;
}
}
}
}
️优化:对于pre<i,由于preThe record is the subscript of the previous number,Then the lower recursive loop,直接让i=pre+1,去掉对1~pre这部分的if判断,不然每次for循环都是1-n的判断.The following topics will also be used in the following way
//递归,修改i=pre+1
for (int i = pre + 1; i <= n; i++) {
//剪枝
if(k - layer > n - i) {
return;
}
record[i] = true;
dfs(n, k, i, layer + 1);
record[i] = false;
}
39. 组合总和
Given an array with no repeating elements,Find the element sum for target的所有组合,And each element can be used multiple times in a combination
思路:DFS,回溯
- Although the title says the same element can be reused,But the order is still immutable,也就是12和21is the same combination.跟上一题一样,The same applies to the order problempreto record the previous element,due to repeatability,需要讲
i=pre+1 改为 i=pre - Since the size of each combination is uncertain,Not suitable for record arrays
record进行标记,Can be replaced by a collection,Select to add to the end of the collection,Remove from end without selection. - Pruning has also changed,This is related to the solution goal,That is, the sum of the combinations must be equaltarget,That means that the greater than the direct skip.(不是return,因为这里candidatesThe elements of an array are not necessarily ordered,You can't guarantee that the following elements are necessarily larger,除非,You use quicksort first)
class Solution {
//记录每个组合
private List<Integer> zuhe;
//结果
private List<List<Integer>> res;
public List<List<Integer>> combinationSum(int[] candidates, int target) {
res = new ArrayList<>();
zuhe = new ArrayList<>();
dfs(candidates, target, 0, 0);
return res;
}
private void dfs(int[] candidates, int target, int sum, int pre) {
if (sum == target) {
res.add(new ArrayList<>(zuhe));
return;
}
int l = candidates.length;
//Due to repeatable selection,i=pre
for (int i = pre; i < l; i++) {
//剪枝
if(sum + candidates[i] > target) {
continue;
}
zuhe.add(candidates[i]); //选择添加
dfs(candidates, target, sum + candidates[i], i);
zuhe.remove(zuhe.size() - 1); //Uncheck Remove
}
}
}
The first two questions are for no repeating elements
40. 组合总和 II
Given an array with duplicate elements,Find the element sum for target的组合,And each element cannot be reused
思路:DFS,回溯
- Since each element is not reusable,跟第一道题类似,通过preSaves the subscript of the previous element,This way the next layer is traversedi=pre+1This avoids revisiting the previous element.
- But there is still one big problem with this question,The array has duplicate elements,例如,1121,target=3,会出现1211和1211的情况(preIt's just a matter of ensuring access order),The problem is that the access to the repeated numbers is not in order,也就是对于21,1is preceded by a repeating number,But haven't visited yet,At this point, if the access is repeated,So we only need to guarantee access when repeating numbers,The repeating numbers in front of it must be visited.The specific method is to compare with the previous number(The premise is that the array needs to be sorted)例如1211排序后就是1112,If the first number of the combination number is selectedi=1,此时
[i]==[i-1],That is to exist0The number of duplicates has not been visited yet,I am not eligible to visit,继续下一个,i=2,此时[i]==[i-1], Not eligible to visit,只有i=0was visited,i=1才能访问,i=1访问过,i=2才能访问.The essence is that the guarantee is in the recursion tree,Points on the same level cannot have duplicate elements.大体如下图,Red means inaccessible.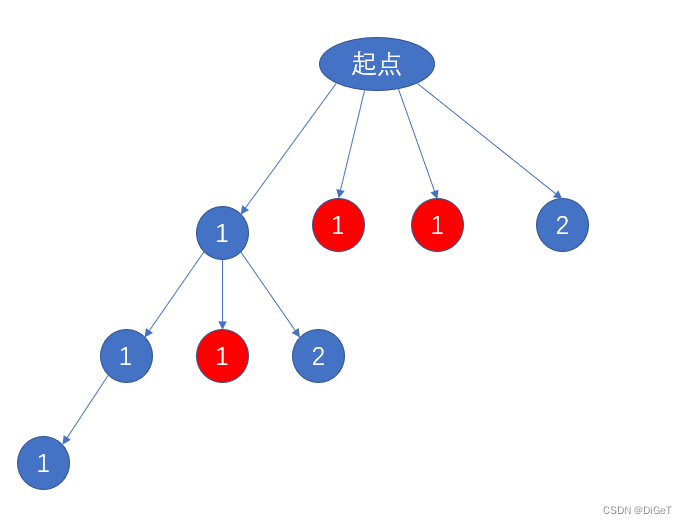
- Since the size of each combination is uncertain,Similarly, use a collection to save the combined result,Select to add to the end of the collection,Remove from end without selection.
- 剪枝,同上,And here can be directlyreturn,因为数组有序,往后遍历,The result will only be bigger
class Solution {
private List<Integer> zuhe;
private List<List<Integer>> res;
public List<List<Integer>> combinationSum2(int[] candidates, int target) {
res = new ArrayList<>();
zuhe = new ArrayList<>();
//排序
Arrays.sort(candidates);
//pre为-1是因为数组下标从0开始,注意和第一题的区别
dfs(candidates, target, 0, -1);
return res;
}
private void dfs(int[] candidates, int target, int sum, int pre) {
if (sum == target) {
res.add(new ArrayList<>(zuhe));
return;
}
int l = candidates.length;
for (int i = pre+1; i < l; i++) {
//pre+1不需要判断,Because the previous element must have been visited(上一层)
if(i>pre+1 && candidates[i]==candidates[i-1]) continue;
//剪枝
if(sum + candidates[i] > target) {
return; //直接返回
}
zuhe.add(candidates[i]); //添加
dfs(candidates, target, sum + candidates[i], i);
zuhe.remove(zuhe.size() - 1); //移除
}
}
}
216. 组合总和 III
给定1-9的数组,挑出kThe number constitutes and isn的组合,And each element can only be used once in the composition.
compared to the previous two,This one is rather simple.
思路:DFS,回溯
- Same as the first combination,数组是固定的,It's just the sum of the combinations,The same applies to the order problempreto record the previous element
- The combined size is determined,An array of records can be used
record进行标记,Collections are also available - There are two prunings,When the combined sum is equal totarget,That means greater than is returned directly.There is also the number of elements,也就是
k > 10-i直接返回,这里用k递减,So there is no first questionlayer
class Solution {
private List<Integer> record;
private List<List<Integer>> res;
public List<List<Integer>> combinationSum3(int k, int n) {
record = new ArrayList<>();
res = new ArrayList<>();
dfs(k, n, 0, 0);
return res;
}
public void dfs(int k, int n, int sum, int pre) {
//边界
if (k == 0 && sum == n) {
res.add(new ArrayList<>(record));
return;
}
for (int i = pre + 1; i <= 9; i++) {
//剪枝
if (sum + i > n || k > 10-i) {
return;
}
record.add(i); //添加
dfs(k - 1, n, sum + i, i);
record.remove(record.size() - 1); //移除
}
}
}
377. 组合总和 Ⅳ
Given an array with no repeating elements,Find the element sum for targetthe number of all combinations of ,And each element can be used multiple times in a combination,且112和211不一样,Because there is no order,所以不需要pre,但是需要剪枝,因为数据过大,容易超时.
https://leetcode.cn/problems/combination-sum-iv/
思路:dfs + 缓存(Also known as memoized search on the Internet),In fact, it is to save some recursive results,Thereby avoiding double calculation by pruning
例如:如果不缓存,The following example times out
[10,20,30,40,50,60,70,80,90,100,110,120,130,140,150,160,170,180,190,200,210,220,230,240,250,260,270,280,290,300,310,320,330,340,350,360,370,380,390,400,410,420,430,440,450,460,470,480,490,500,510,520,530,540,550,560,570,580,590,600,610,620,630,640,650,660,670,680,690,700,710,720,730,740,750,760,770,780,790,800,810,820,830,840,850,860,870,880,890,900,910,920,930,940,950,960,970,980,990,111]
999
class Solution {
//Record remaining value cache
int[] cache;
public int combinationSum4(int[] nums, int target) {
cache = new int[target+1];
//Note that initialization cannot be0,因为0也可以缓存,你如果用hashmap就知道为什么了,因为hashmap也会对0进行缓存
Arrays.fill(cache, -1);
int count = dfs(nums,target);
return count;
}
public int dfs(int[] nums, int rest) {
if(rest == 0) {
return 1;
}
//错误判断if(cache[rest] != 0)
//Prune according to cache,正确的判断
if(cache[rest] != -1) return cache[rest];
int l = nums.length;
int sum = 0;
for(int i = 0; i < l; i++) {
if(nums[i] <= rest) {
sum += dfs(nums, rest - nums[i]);
}
}
cache[rest] = sum; //缓存
return sum;
}
}
边栏推荐
- BigDecimal 简介,常用方法
- MySQL 23道经典面试吊打面试官
- Shell script classic case: detecting whether a batch of hosts is alive
- LeetCode旋转数组
- 深度剖析 Apache EventMesh 云原生分布式事件驱动架构
- Controller层代码这么写,简洁又优雅!
- 技能大赛dhcp服务训练题
- C# control StatusStrip use
- Comparison of Optical Motion Capture and UWB Positioning Technology in Multi-agent Cooperative Control Research
- Nuget打包并上传教程
猜你喜欢

go使用makefile脚本编译应用

The JVM a class loader

Linux bash: redis-server: command not found
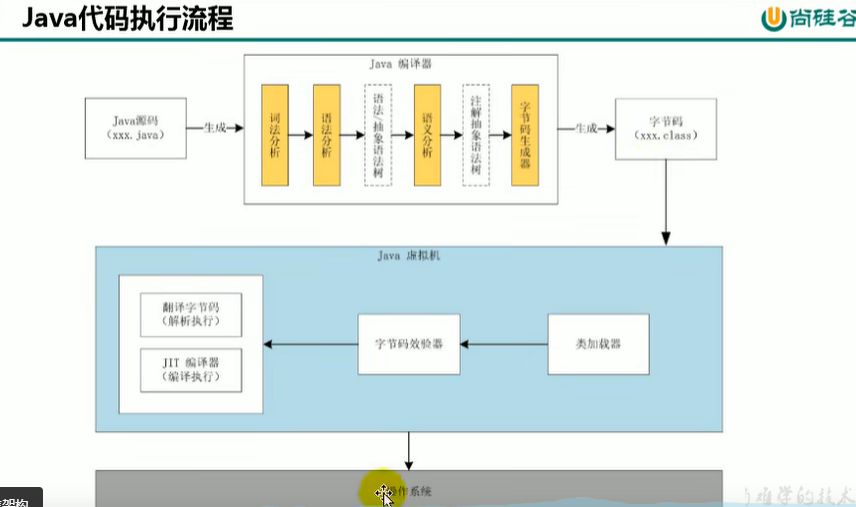
尚硅谷-JVM-内存和垃圾回收篇(P1~P203)
以后面试官问你 为啥不建议使用Select *,请你大声回答他!

LeetCode·304竞赛·6132·使数组中所有元素都等于零·模拟·哈希
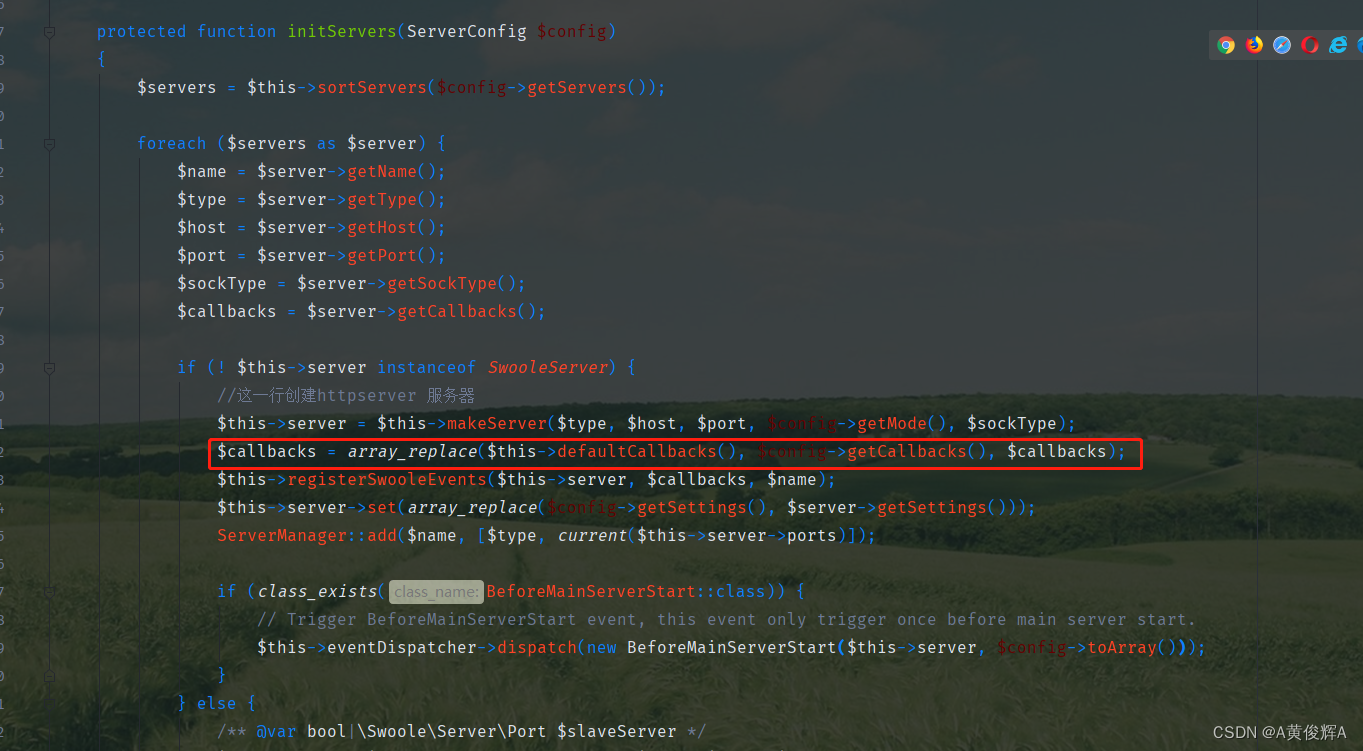
Analysis of the startup source code of hyperf (2) - how the request reaches the controller

技能大赛训练题:域用户和组织单元的创建

ICML2022 | 面向自监督图表示学习的全粒度自语义传播

In the future, the interviewer asks you why it is not recommended to use Select *, please answer him out loud!
随机推荐
技能大赛训练题:登录安全加固
Shell脚本经典案例:探测批量主机是否存活
推荐系统-召回阶段-2013:DSSM(双塔模型)【Embedding(语义向量)召回】【微软】
深度剖析 Apache EventMesh 云原生分布式事件驱动架构
MySQL玩到这种程度,难怪大厂抢着要!
A detailed explanation of the usage of Async and Await in C#
技能大赛训练题:MS15_034漏洞验证与安全加固
The use of C# control CheckBox
C# control ToolStripProgressBar usage
numpy矩阵和向量的保存与加载,以及使用保存的向量进行相似度计算
DELL SC compellent 康贝存储系统怎么抓取配置信息
LeetCode·每日一题·1161.最大层内元素和·层次遍历
Six Stones Programming: No matter which function you think is useless, people who can use it will not be able to leave, so at least 99%
技能大赛训练题:ftp 服务攻防与加固
What should I do if selenium is reversed?
最新完整代码:使用word2vec预训练模型进行增量训练(两种保存方式对应的两种加载方式)适用gensim各种版本
ECCV 2022 | Robotic Interaction Perception and Object Manipulation
[Blue Bridge Cup Trial Question 46] Scratch Magnet Game Children's Programming Scratch Blue Bridge Cup Trial Question Explanation
ICML2022 | Fully Granular Self-Semantic Propagation for Self-Supervised Graph Representation Learning
【redis】发布和订阅消息