当前位置:网站首页>4 solutions de court - circuit et 2 solutions d'arbre de génération minimum
4 solutions de court - circuit et 2 solutions d'arbre de génération minimum
2022-06-22 07:34:00 【_ Bar _ Light Maison】
Catalogue des articles
Version simpleDijkstra
- O(n^2),Pour les cartes denses,Utiliser la matrice de contiguïté
- Chaque fois qu'on en trouve unLe plus proche du point sourcePoint
- Ajouter ce point àCollection de circuits les plus courtsMoyenne
- Utilisez ce point pour mettre à jour la distance entre les autres points et le point source
Heap Optimized EditionDijkstra
- O(mlogm),Pour les diagrammes clairsemés,Utiliser la liste de contiguïté
- Chaque foisDe petits tas de racinesObtenir le point le plus proche du point source
- Ajoutez ce point à la collection la plus courte
- Utilisez ce point pour mettre à jour la distance entre le point accessible à partir de ce point et le point source
Bellman-Ford
- O(nm),Souvent utilisé pour les courts - circuits avec un nombre limité de fois,UtiliserEdgeStructure
- .Ajoutez tous les points à la file d'attente
- Mise à jourkUne fois,Tous les points serontMise à jour
Spfa
- Mieux vautO(n),Au pireO(nm),Il est possible de déterminer s'il y a une boucle de puissance négative
- Ajouter le point source à la file d'attente
- Utilisez le point source pour mettre à jour les autres points ,Et va Les points mis à jour sont mis en file d'attente , Prochain tour pour mettre à jour les autres points . Où, pour s'assurer que les mêmes différences ne sont pas mises en file d'attente à plusieurs reprises dans le même cycle ,Peut être utilisé
boolean[]
Kruskal
- O(mlogm),Pour les diagrammes clairsemés,UtiliserEdgeStructure
- Mettez tous les côtés Par ordre croissant de poids
- De l'enfance à l'élection générale, joignez - vous à l'arbre de production minimal , Si le point appartient à un ensemble différent , Ajoutez les différences à la même collection , Pour former une collection
Prim
- O(n^2),Pour les cartes denses,Utiliser la matrice de contiguïté
- Chaque fois qu'on en trouve un qui s'éloigne Collection de points sources Le point le plus proche
- Ajoutez ce point à la collection d'arbres de construction minimale
- Utilisez ce point pour mettre à jour d'autres points à Collection de points sources Distance de
DijkstraPour le court - circuit
Compte tenu d'un nn Un point mm Un digraphe à côté d'une barre,Il peut y avoir des bords lourds et des autoanneaux dans la figure,Tous les poids latéraux sont positifs.
S'il vous plaît, trouvez 11 Le numéro est arrivé. nn La plus courte distance du point,Si vous ne pouvez pas 11 Le point n°1 est arrivé à nn Point No,Alors la sortie −1−1.
- Format d'entrée
La première ligne contient un entier nn Et mm.
Et puis... mm Ligne contient trois entiers par ligne x,y,zx,y,z,Indique qu'il y a un point esclave xx Au point yy Le bord dirigé de,La longueur latérale est zz.
- Format de sortie
Sortie d'un entier,Représentation 11 Le numéro est arrivé. nn La plus courte distance du point.
Si le chemin n'existe pas,Alors la sortie −1−1.
- Champ d'application des données
1≤n≤5001≤n≤500,
1≤m≤1051≤m≤105,
La longueur latérale n'est pas supérieure à10000.
- Exemple d'entrée:
3 3
1 2 2
2 3 1
1 3 4
- Exemple de sortie:
3
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStream;
import java.io.InputStreamReader;
import java.util.Arrays;
public class Main {
final static int INF = 0x3f3f3f3f;
static int n, m;
static int[][] g;
public static void main(String[] args) throws IOException {
BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
String[] cur = in.readLine().split(" ");
n = Integer.parseInt(cur[0]);
m = Integer.parseInt(cur[1]);
g = new int[n + 1][n + 1];
for (int i = 0; i <= n; i ++) {
Arrays.fill(g[i], INF);
}
for (int i = 0; i < m; i ++) {
String[] str = in.readLine().split(" ");
int a = Integer.parseInt(str[0]);
int b = Integer.parseInt(str[1]);
int c = Integer.parseInt(str[2]);
g[a][b] = Math.min(g[a][b], c);
}
Dijkstra();
}
public static void Dijkstra() {
boolean[] vis = new boolean[n + 1];
int[] dist = new int[n + 1];
Arrays.fill(dist, INF);
dist[1] = 0;
for (int i = 1; i <= n; i ++) {
int t = -1;
for (int j = 1; j <= n; j ++) {
if (!vis[j] && (t == -1 || dist[t] > dist[j])) {
t = j;
}
}
vis[t] = true;
for (int j = 1; j <= n; j ++) {
dist[j] = Math.min(dist[j], dist[t] + g[t][j]);
}
}
if (dist[n] == INF) System.out.println("-1");
else System.out.println(dist[n]);
}
}
Heap OptimizedDijkstraPour le court - circuit
Compte tenu d'un nn Un point mm Un digraphe à côté d'une barre,Il peut y avoir des bords lourds et des autoanneaux dans la figure, Tous les poids latéraux sont non négatifs .
S'il vous plaît, trouvez 11 Le numéro est arrivé. nn La plus courte distance du point,Si vous ne pouvez pas 11 Le point n°1 est arrivé à nn Point No,Alors la sortie −1−1.
- Format d'entrée
La première ligne contient un entier nn Et mm.
Et puis... mm Ligne contient trois entiers par ligne x,y,zx,y,z,Indique qu'il y a un point esclave xx Au point yy Le bord dirigé de,La longueur latérale est zz.
- Format de sortie
Sortie d'un entier,Représentation 11 Le numéro est arrivé. nn La plus courte distance du point.
Si le chemin n'existe pas,Alors la sortie −1−1.
- Champ d'application des données
1≤n,m≤1.5×1051≤n,m≤1.5×105,
La longueur latérale n'est pas inférieure à 00,Et pas plus de 1000010000.
Garantie des données: Si le court - circuit existe , La longueur du circuit le plus court ne doit pas dépasser 109109.
- Exemple d'entrée:
3 3
1 2 2
2 3 1
1 3 4
- Exemple de sortie:
3
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStream;
import java.io.InputStreamReader;
import java.util.Arrays;
import java.util.Comparator;
import java.util.PriorityQueue;
// Heap Optimized EditionDijkstra
public class Main {
static int n, m;
static int N = 150010;
// idx Indique le noeud actuel
// he[i]Exprimé pari Le noeud d'en - tête de la liste de liens commençant par le noeud est le bord numéro ,e[idx]Indique le paragrapheidx Quel Sommet pointe le bord dirigé de la barre
// ne[idx]Indique le paragrapheidx Le bord dirigé de la table pointe vers le noeud de la liste liée ,w[idx]Indique le paragrapheidx Poids des bords des bandes avec des bords orientés
static int idx = 0;
static int[] he = new int[N], e = new int[N], ne = new int[N], w = new int[N];
static void add(int a, int b, int c) {
e[idx] = b; w[idx] = c; ne[idx] = he[a]; he[a] = idx ++;
}
static int[] dist = new int[N];
static boolean[] vis = new boolean[N];
static int INF = 0x3f3f3f3f;
public static void main(String[] args) throws IOException {
BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
String[] cur = in.readLine().split(" ");
n = Integer.parseInt(cur[0]);
m = Integer.parseInt(cur[1]);
for (int i = 0; i <= n; i ++) {
he[i] = -1;
}
for (int i = 0; i < m; i ++) {
String[] str = in.readLine().split(" ");
int a = Integer.parseInt(str[0]);
int b = Integer.parseInt(str[1]);
int c = Integer.parseInt(str[2]);
add(a, b, c);
}
Dijkstra();
}
public static void Dijkstra() {
for (int i = 0; i <= n; i ++) {
dist[i] = INF;
}
dist[1] = 0;
PriorityQueue<int[]> q = new PriorityQueue<>(new Comparator<int[]>() {
@Override
public int compare(int[] a, int[] b) {
return a[0] - b[0];
}
});
// int[] Le premier paramètre est Vertex to 1 La distance du , Le deuxième paramètre est le numéro Vertex
q.add(new int[]{
0, 1});
while (!q.isEmpty()) {
int[] top = q.poll();
int distance = top[0], vertex = top[1];
if (vis[vertex]) continue;
vis[vertex] = true;
// Traverser pourvertex Tous les bords dirigés au début du Vertex ,i C'est un numéro avec des bords orientés
for (int i = he[vertex]; i != -1; i = ne[i]) {
int j = e[i];
if (distance + w[i] < dist[j]) {
dist[j] = distance + w[i];
q.add(new int[]{
dist[j], j});
}
}
}
if (dist[n] == INF) System.out.println("-1");
else System.out.println(dist[n]);
}
}
Bellman-fordPour le court - circuit
Compte tenu d'un nn Un point mm Un digraphe à côté d'une barre,Il peut y avoir des bords lourds et des autoanneaux dans la figure, Les poids latéraux peuvent être négatifs.
S'il vous plaît, trouvez à partir de 11 Le numéro est arrivé. nn Le plus grand nombre de points passant kk La plus courte distance du bord de la barre,Si vous ne pouvez pas 11 Le point n°1 est arrivé à nn Point No,Produits impossible.
Attention!:Possible dans le graphique Il y a une boucle de poids négatif .
- Format d'entrée
La première ligne contient trois entiers n,m,kn,m,k.
Et puis... mm D'accord,Chaque ligne contient trois entiers x,y,zx,y,z,Indique qu'il y a un point esclave xx Au point yy Le bord dirigé de,La longueur latérale est zz.
- Format de sortie
Sortie d'un entier,De 11 Le numéro est arrivé. nn Le plus grand nombre de points passant kk La plus courte distance du bord de la barre.
S'il n'y a pas de chemin satisfaisant,Alors la sortie impossible.
- Champ d'application des données
1≤n,k≤5001≤n,k≤500,
1≤m≤100001≤m≤10000,
La valeur absolue de n'importe quelle longueur latérale ne doit pas dépasser 1000010000.
- Exemple d'entrée:
3 3 1
1 2 1
2 3 1
1 3 3
- Exemple de sortie:
3
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.List;
public class Main {
private static final int INF = 0x3f3f3f3f;
static class Edge {
int a, b, c;
public Edge(int a, int b, int c) {
this.a = a;
this.b = b;
this.c = c;
}
}
static int N = 510, M = 10010;
static int n, m, k;
static List<Edge> list = new ArrayList<>();
static int[] dist = new int[N];
public static void main(String[] args) throws IOException {
BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
String[] cur = in.readLine().split(" ");
n = Integer.parseInt(cur[0]);
m = Integer.parseInt(cur[1]);
k = Integer.parseInt(cur[2]);
for (int i = 0; i < m; i ++) {
String[] str = in.readLine().split(" ");
int a = Integer.parseInt(str[0]);
int b = Integer.parseInt(str[1]);
int c = Integer.parseInt(str[2]);
list.add(new Edge(a, b, c));
}
BellmanFord();
}
public static void BellmanFord() {
for (int i = 0; i <= n; i ++) {
dist[i] = INF;
}
dist[1] = 0;
// En courskMises à jour
for (int i = 0; i < k; i ++) {
// Chaque mise à jour ne peut avoir d'effet de ricochet , C'est pour ça que la dernière fois distUne copie en profondeur
int[] prev = dist.clone();
for (Edge edge : list) {
dist[edge.b] = Math.min(dist[edge.b], prev[edge.a] + edge.c);
}
}
if (dist[n] > INF / 2) System.out.println("impossible");
else System.out.println(dist[n]);
}
}
SpfaPour le court - circuit
Compte tenu d'un nn Un point mm Un digraphe à côté d'une barre,Il peut y avoir des bords lourds et des autoanneaux dans la figure, Les poids latéraux peuvent être négatifs.
S'il vous plaît, trouvez 11 Le numéro est arrivé. nn La plus courte distance du point,Si vous ne pouvez pas 11 Le point n°1 est arrivé à nn Point No,Alors la sortie impossible.
Garantie des données il n'y a pas de boucle de pondération négative.
- Format d'entrée
La première ligne contient un entier nn Et mm.
Et puis... mm Ligne contient trois entiers par ligne x,y,zx,y,z,Indique qu'il y a un point esclave xx Au point yy Le bord dirigé de,La longueur latérale est zz.
- Format de sortie
Sortie d'un entier,Représentation 11 Le numéro est arrivé. nn La plus courte distance du point.
Si le chemin n'existe pas,Alors la sortie impossible.
- Champ d'application des données
1≤n,m≤1051≤n,m≤105,
Les valeurs absolues des longueurs latérales ne doivent pas dépasser 1000010000.
- Exemple d'entrée:
3 3
1 2 5
2 3 -3
1 3 4
- Exemple de sortie:
2
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.Deque;
import java.util.LinkedList;
import java.util.List;
class Main {
private static final int INF = 0x3f3f3f3f;
static int n, m;
static int N = 100010;
static int[] he = new int[N], e = new int[N], w = new int[N], ne = new int[N];
static int idx = 0;
static int[] dist = new int[N];
static boolean[] vis = new boolean[N];
public static void add(int a, int b, int c) {
e[idx] = b; w[idx] = c; ne[idx] = he[a]; he[a] = idx ++;
}
public static void main(String[] args) throws IOException {
BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
String[] cur = in.readLine().split(" ");
n = Integer.parseInt(cur[0]);
m = Integer.parseInt(cur[1]);
for (int i = 0; i <= n; i ++) {
he[i] = -1;
}
for (int i = 0; i < m; i ++) {
String[] str = in.readLine().split(" ");
int a = Integer.parseInt(str[0]);
int b = Integer.parseInt(str[1]);
int c = Integer.parseInt(str[2]);
add(a, b, c);
}
Spfa();
}
public static void Spfa() {
for (int i = 0; i <= n; i ++) {
dist[i] = INF;
}
dist[1] = 0;
vis[1] = true;
Deque<Integer> q = new LinkedList<>();
q.add(1);
// Utiliservis Le tableau est conçu pour empêcher les noeuds qui sont actuellement dans la file d'attente , Pas besoin d'être ajouté à la file d'attente à plusieurs reprises
// .Mais comme un Vertex peut être utilisé pour mettre à jour le chemin plusieurs fois , Donc après chaque mise à jour du chemin avec un Vertex
// Il faut aussivis[ver]=false, Afin que le Vertex puisse être mis à jour la prochaine fois
while (!q.isEmpty()) {
int ver = q.pollFirst();
vis[ver] = false;
for (int i = he[ver]; i != -1; i = ne[i]) {
int j = e[i];
if (w[i] + dist[ver] < dist[j]) {
dist[j] = w[i] + dist[ver];
if (!vis[j]) {
vis[j] = true;
q.add(j);
}
}
}
}
if (dist[n] > INF / 2) System.out.println("impossible");
else System.out.println(dist[n]);
}
}
Dijkstra Pourquoi ne pas calculer un graphique avec des bords avec des poids négatifs ?
- Dijkstra C'est basé sur une stratégie gourmande , Sélectionnez le point le plus proche du point courant à chaque fois , Utilisez ce point pour mettre à jour d'autres points . Mais si les bords du graphique ont un nombre négatif , Le point le plus proche n'est peut - être pas le meilleur choix , Au lieu du point le plus proche, il est possible que le chemin et la diminution du bord négatif .
- ![[Pasted image 20220616104956.png]]
DijkstraEtSpfaLes différences d'écriture?
- DijkstraEtSpfa C'est écrit comme , Mais le sens est complètement différent . Qu'il s'agisse d'une version simple Dijkstra Encore une version optimisée du tas Dijkstra, Chaque fois que vous obtenez le point le plus proche du point source et non mis à jour , Puis utilisez ce point pour mettre à jour d'autres chemins .MaisSpfa Chaque fois, ce n'est que le dernier point mis à jour ,Dans la file d'attente( Ou d'autres structures de données ), Utilisez ces points mis à jour pour mettre à jour d'autres points .
- Relativement parlant, Basé sur la cupidité Dijkstra Mettre davantage l'accent sur la solution optimale locale ,EtSpfa Tout ce qui compte, c'est le court - circuit Final ,Alors...Spfa La structure globale de l'algorithme est plus détendue . C'est aussi pour ça que Spfa Un graphique capable de traiter des bords pondérés négatifs .
SpafaDéterminer la boucle de puissance négative
Compte tenu d'un nn Un point mm Un digraphe à côté d'une barre,Il peut y avoir des bords lourds et des autoanneaux dans la figure, Les poids latéraux peuvent être négatifs.
Veuillez déterminer s'il y a une boucle de poids négatif dans le diagramme.
- Format d'entrée
La première ligne contient un entier nn Et mm.
Et puis... mm Ligne contient trois entiers par ligne x,y,zx,y,z,Indique qu'il y a un point esclave xx Au point yy Le bord dirigé de,La longueur latérale est zz.
- Format de sortie
Si le graphiqueExisteBoucle de puissance négative,Alors la sortie Yes,Sinon, la sortie No.
- Champ d'application des données
1≤n≤20001≤n≤2000,
1≤m≤100001≤m≤10000,
Les valeurs absolues des longueurs latérales ne doivent pas dépasser 1000010000.
- Exemple d'entrée:
3 3
1 2 -1
2 3 4
3 1 -4
- Exemple de sortie:
Yes
- Parce quemC'est énorme., Ça veut dire qu'il y a beaucoup de côtés , Il est donc préférable d'utiliser la liste de contiguïté .
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.Deque;
import java.util.LinkedList;
class Main {
private static final int INF = 0x3f3f3f3f;
static int n, m;
static int N = 100010;
static int[] he = new int[N], e = new int[N], w = new int[N], ne = new int[N];
static int idx = 0;
static int[] dist = new int[N];
static boolean[] vis = new boolean[N];
// cnt[i]Représentationi Nombre de bords du chemin le plus court du Vertex à l'origine
// Sicnt[i]>=nEt si,Descriptioni Le nombre de bords de la plus courte distance entre le Sommet et l'origine dépasse n, Au moins un point a été utilisé n+1Une fois
// Il y a une boucle , Et un nombre positif ne peut pas avoir de boucle , Description la boucle de poids négatif apparaît sur la figure
static int[] cnt = new int[N];
public static void add(int a, int b, int c) {
e[idx] = b; w[idx] = c; ne[idx] = he[a]; he[a] = idx ++;
}
public static void main(String[] args) throws IOException {
BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
String[] cur = in.readLine().split(" ");
n = Integer.parseInt(cur[0]);
m = Integer.parseInt(cur[1]);
for (int i = 0; i <= n; i ++) {
he[i] = -1;
}
for (int i = 0; i < m; i ++) {
String[] str = in.readLine().split(" ");
int a = Integer.parseInt(str[0]);
int b = Integer.parseInt(str[1]);
int c = Integer.parseInt(str[2]);
add(a, b, c);
}
if(Spfa()) System.out.println("Yes");
else System.out.println("No");
}
public static boolean Spfa() {
// dist Le tableau peut être initialisé ou non , Parce que si une boucle négative se produit ,dist[i] Tout sera mis à jour
for (int i = 0; i <= n; i ++) {
dist[i] = INF;
}
Deque<Integer> q = new LinkedList<>();
// Pour éviter qu'un point ne puisse atteindre la boucle de puissance négative , Il faut donc tenir compte de tous les chemins , Tous les sommets doivent donc être mis en file d'attente pour vérification
for (int i = 1; i <= n; i ++) {
vis[i] = true;
q.add(i);
}
while (!q.isEmpty()) {
int ver = q.pollFirst();
vis[ver] = false;
for (int i = he[ver]; i != -1; i = ne[i]) {
int j = e[i];
if (dist[j] > dist[ver] + w[i]) {
dist[j] = dist[ver] + w[i];
// Chaque fois quej Les sommets sont mis à jour ,DescriptionverPoint.j Le chemin le plus court sur le point a un bord de plus
cnt[j] = cnt[ver] + 1;
if (cnt[j] > n) return true;
if (!vis[j]) {
vis[j] = true;
q.add(j);
}
}
}
}
return false;
}
}
- Attention!: Ceci n'est écrit que pour vérifier l'existence d'une boucle dans le chemin , Il n'y a donc pas de norme Spfa Calculer le court - circuit et écrire .
FloydPour le court - circuit
Compte tenu d'un nn Un point mm Un digraphe à côté d'une barre,Il peut y avoir des bords lourds et des autoanneaux dans la figure,Les poids latéraux peuvent être négatifs.
Encore une fois kk Questions,Chaque requête contient deux entiers xx Et yy,Représente la requête à partir du point xx Au point yy La plus courte distance de,Si le chemin n'existe pas,Alors la sortie impossible.
Il n'y a pas de boucle de poids négatif dans le diagramme de garantie des données.
- Format d'entrée
La première ligne contient trois entiers n,m,kn,m,k.
Et puis... mm D'accord,Chaque ligne contient trois entiers x,y,zx,y,z,Indique qu'il y a un point esclave xx Au point yy Le bord dirigé de,La longueur latérale est zz.
Et puis... kk D'accord,Chaque ligne contient deux entiers x,yx,y,Indique le point d'interrogation xx Au point yy La plus courte distance de.
- Format de sortie
Total kk D'accord,Un entier par ligne,Indique le résultat de l'enquête,Si vous demandez qu'il n'y a pas de chemin entre deux points,Alors la sortie impossible.
- Champ d'application des données
1≤n≤2001≤n≤200,
1≤k≤n21≤k≤n2
1≤m≤200001≤m≤20000,
Les valeurs absolues des longueurs latérales ne doivent pas dépasser 1000010000.
- Exemple d'entrée:
3 3 2
1 2 1
2 3 2
1 3 1
2 1
1 3
- Exemple de sortie:
impossible
1
[[Planification dynamique]]
dp[k][i][j]Indique que le court - circuit est considéré comme k Noeud comme noeud de passage intermédiaire .- Formule récursive:
dp[k][i][j] = Math.min(dp[k-1][i][j], dp[k-1][i][k]+dp[k-1][k][j]),dp[k-1][i][j]DeiÀjNon.kLe chemin le plus court du noeuddp[k-1][i][k]+dp[k-1][k][j]DeiÀkEncore.jLe chemin le plus court vers.
- Parce que dans la formule récursive
dp[k]Seulement avecdp[k-1]Concernant, Et calculédp[k][i][j]Ça va devenir plus petit ,Sans préjudice du résultat final, Ainsi, la limitation de l'espace unidimensionnel peut être évitée .dp[i][j]=Math.min(dp[i][j], dp[i][k]+dp[k][j]), Mais l'ordre des cycles ne peut pas être modifié , Encore une fois, bouclez d'abord la variable de noeud intermédiairek.
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
class Main {
static int N = 210;
static int[][] g = new int[N][N];
static int n, m, k;
static int INF = 0x3f3f3f3f;
public static void main(String[] args) throws IOException {
BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
String[] cur = in.readLine().split(" ");
n = Integer.parseInt(cur[0]);
m = Integer.parseInt(cur[1]);
k = Integer.parseInt(cur[2]);
// Attention, si vous utilisez floyd, Assurez - vous que la distance entre les sommets et vous - même est 0
for (int i = 0; i <= n; i ++) {
for (int j = 0; j <= n; j ++) {
if (i == j) g[i][j] = 0;
else g[i][j] = INF;
}
}
for (int i = 0; i < m; i ++) {
String[] str = in.readLine().split(" ");
int a = Integer.parseInt(str[0]);
int b = Integer.parseInt(str[1]);
int c = Integer.parseInt(str[2]);
g[a][b] = Math.min(g[a][b], c);
}
Floyd();
while (k -- > 0) {
String[] str = in.readLine().split(" ");
int a = Integer.parseInt(str[0]);
int b = Integer.parseInt(str[1]);
if (g[a][b] == INF) System.out.println("impossible");
else System.out.println(g[a][b]);
}
}
public static void Floyd() {
for (int k = 1; k <= n; k ++) {
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
g[i][j] = Math.min(g[i][j], g[i][k] + g[k][j]);
}
}
}
}
}
KruskalTrouver l'arbre de génération minimal
Compte tenu d'un nn Un point mm Un graphique non rectiligne avec des bords,Il peut y avoir des bords lourds et des autoanneaux dans la figure,Les poids latéraux peuvent être négatifs.
Trouver la somme des poids des bords de l'arbre qui produisent le moins d'arbres,Sortie si l'arbre de construction minimal n'existe pas impossible.
Compte tenu d'un graphique non recté pondéré G=(V,E)G=(V,E),Parmi eux VV Une collection représentant le point médian d'un graphique,EE Représente une collection de bords dans le graphique,n=|V|n=|V|,m=|E|m=|E|.
Par VV Tous les nn Sommets et EE Moyenne n−1n−1 Le Sous - graphe connecté non directionnel formé par les bords des bandes est appelé GG Un arbre générant,L'arbre générant le moins de la somme des poids des bords est appelé un Graphe non recté GG Arbre de production minimal pour.
- Format d'entrée
La première ligne contient deux entiers nn Et mm.
Et puis... mm D'accord,Chaque ligne contient trois entiers u,v,wu,v,w,Point de représentation uu Et point vv Il y a un poids entre ww Le bord de.
- Format de sortie
Sur une ligne,S'il y a un arbre de construction minimal,Un entier est sorti,Représente la somme des poids des bords de l'arbre pour le plus petit arbre généré,Sortie si l'arbre de construction minimal n'existe pas impossible.
- Champ d'application des données
1≤n≤1051≤n≤105,
1≤m≤2∗1051≤m≤2∗105,
Aucune des valeurs absolues des poids des bords impliqués dans le dessin ne dépasse 10001000.
- Exemple d'entrée:
4 5
1 2 1
1 3 2
1 4 3
2 3 2
3 4 4
- Exemple de sortie:
6
[[Ensemble de recherche]]+[[Avidité]]
- Trier les poids des bords , La préférence est donnée aux bords les moins pondérés comme branches de l'arbre générant le moins de poids .
- Les bords sélectionnés pour devenir l'arbre de construction minimal doivent être marqués comme étant déjà sélectionnés ,Mais il ne peut pas être utilisé
boolean[]Marquer. Parce qu'il se peut qu'un bord ait été sélectionné , Mais ce côté n'est qu'un sous - arbre de l'arbre le plus petit , Plus tard, le Sous - arbre sera ajouté à une autre partie de l'arbre le plus petit .Si vous utilisezbooleanLes mots marqués, Une fois qu'un bord est marqué, il ne peut pas être sélectionné ,C'est nécessaire.Utiliser et rechercher des ensembles, La collection à laquelle appartiennent les différents points peut être distinguée .
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.Collections;
import java.util.Comparator;
import java.util.List;
class Main {
static int n, m;
static List<Edge> list = new ArrayList<>();
static int N = 100010, M = 200010;
static boolean[] vis = new boolean[N];
static int[] p = new int[N];
static class Edge {
int a, b, c;
public Edge(int a, int b, int c) {
this.a = a;
this.b = b;
this.c = c;
}
}
public static void main(String[] args) throws IOException {
BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
String[] cur = in.readLine().split(" ");
n = Integer.parseInt(cur[0]);
m = Integer.parseInt(cur[1]);
for (int i = 0; i < m; i ++) {
String[] str = in.readLine().split(" ");
int a = Integer.parseInt(str[0]);
int b = Integer.parseInt(str[1]);
int c = Integer.parseInt(str[2]);
list.add(new Edge(a, b, c));
}
kruskal();
}
public static void kruskal() {
// Initialiser et rechercher l'ensemble
for (int i = 0; i <= n; i ++) {
p[i] = i;
}
Collections.sort(list, new Comparator<Edge>(){
public int compare(Edge a, Edge b) {
return a.c - b.c;
}
});
// cnt Représente le nombre de bords dans l'arbre de génération minimal actuel
// Bien qu'il y ait deux façons de juger de l'arbre de production minimal , Un nombre de bords utilisés , Un nombre de points d'utilisation . Parce que le nombre de sommets dans chaque assemblage ajouté peut être 1Ou2- Oui., Donc nous utilisons le côté statistique pour déterminer
int cnt = 0;
int ans = 0;
for (Edge edge : list) {
int a = edge.a, b = edge.b;
// Trouver la collection à laquelle appartient le Vertex lui - même , Si les sommets appartiennent à une collection différente , Ajoutez les sommets à la même collection
a = find(a);
b = find(b);
if (a != b) {
p[a] = b;
cnt ++;
ans += edge.c;
}
}
if (cnt == n - 1) System.out.println(ans);
else System.out.println("impossible");
}
public static int find(int x) {
if (x != p[x]) p[x] = find(p[x]);
return p[x];
}
}
PrimTrouver l'arbre de génération minimal
Compte tenu d'un nn Un point mm Un graphique non rectiligne avec des bords,Il peut y avoir des bords lourds et des autoanneaux dans la figure,Les poids latéraux peuvent être négatifs.
Trouver la somme des poids des bords de l'arbre qui produisent le moins d'arbres,Sortie si l'arbre de construction minimal n'existe pas impossible.
Compte tenu d'un graphique non recté pondéré G=(V,E)G=(V,E),Parmi eux VV Une collection représentant le point médian d'un graphique,EE Représente une collection de bords dans le graphique,n=|V|n=|V|,m=|E|m=|E|.
Par VV Tous les nn Sommets et EE Moyenne n−1n−1 Le Sous - graphe connecté non directionnel formé par les bords des bandes est appelé GG Un arbre générant,L'arbre générant le moins de la somme des poids des bords est appelé un Graphe non recté GG Arbre de production minimal pour.
- Format d'entrée
La première ligne contient deux entiers nn Et mm.
Et puis... mm D'accord,Chaque ligne contient trois entiers u,v,wu,v,w,Point de représentation uu Et point vv Il y a un poids entre ww Le bord de.
- Format de sortie
Sur une ligne,S'il y a un arbre de construction minimal,Un entier est sorti,Représente la somme des poids des bords de l'arbre pour le plus petit arbre généré,Sortie si l'arbre de construction minimal n'existe pas impossible.
- Champ d'application des données
1≤n≤5001≤n≤500,
1≤m≤1051≤m≤105,
Aucune des valeurs absolues des poids des bords impliqués dans le dessin ne dépasse 1000010000.
- Exemple d'entrée:
4 5
1 2 1
1 3 2
1 4 3
2 3 2
3 4 4
- Exemple de sortie:
6
[[Avidité]]
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
class Main {
static int n, m;
static int N = 510;
static int[][] g = new int[N][N];
static int INF = 0x3f3f3f3f;
static int[] dist = new int[N];
static boolean[] vis = new boolean[N];
public static void main(String[] args) throws IOException {
BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
String[] cur = in.readLine().split(" ");
n = Integer.parseInt(cur[0]);
m = Integer.parseInt(cur[1]);
for (int i = 0; i <= n; i ++) {
for (int j = 0; j <= n; j ++) {
if (i == j) g[i][j] = 0;
else g[i][j] = INF;
}
}
for (int i = 0; i < m; i ++) {
String[] str = in.readLine().split(" ");
int a = Integer.parseInt(str[0]);
int b = Integer.parseInt(str[1]);
int c = Integer.parseInt(str[2]);
g[a][b] = g[b][a] = Math.min(g[a][b], c);
}
int ans = prim();
if (ans == INF) System.out.println("impossible");
else System.out.println(ans);
}
public static int prim() {
// dist .Représente la distance entre le Sommet et l'ensemble constitué par le plus petit arbre de construction
for (int i = 0; i <= n; i ++) {
dist[i] = INF;
}
dist[1] = 0;
int ans = 0;
for (int i = 1; i <= n; i ++) {
int t = -1;
for (int j = 1; j <= n; j ++) {
if (!vis[j] && (t == -1 || dist[t] > dist[j])) {
t = j;
}
}
if (dist[t] == INF) return INF;
vis[t] = true;
ans += dist[t];
for (int j = 1; j <= n; j ++) {
// Utilisez le point le plus proche de la partie connectée pour mettre à jour les autres points
if (!vis[j] && dist[j] > g[t][j]) {
dist[j] = g[t][j];
}
}
}
return ans;
}
}
PrimEtDijkstraComparaison
- En termes d'écriture Prim Et la version simple Dijkstra La mise à jour des bords est différente sauf au dernier point d'utilisation , Le reste est presque identique .MaisPrimEtDijkstra La plus grande différence de sens est Prim Choisissez un ensemble de points de départ à la fois ( C'est - à - dire l'ensemble formé par le plus petit arbre de génération )Le point le plus proche. Donc à chaque mise à jour ,
dist[j]À utiliserg[t][j]Pour mettre à jour.Parce que maintenantt Dans la Collection Source ,C'est - à - dire:t Représente l'ensemble des points sources .
边栏推荐
- Wechat games (2)
- 网站是否要修改标题
- 《百度搜索引擎网页质量白皮书》指导网站建设及优化
- 网站的日常维护
- How to view cookies in Chrome browser
- How to import and upload a CSV generated by a third-party platform to a Taobao store
- Antd framework: click the link to reopen the browser page - Basic accumulation
- Notes on advanced combinatorics -- Conclusion
- js实现随机生成16位的密钥——基础积累
- Time string to timestamp
猜你喜欢

DETR3D模型源码导读 & MMDetection3D构建流程

Antd - a-upload-dragger drag upload component - Basic accumulation

Bad slam resolution

How was the coffee supply chain leveled?

True MySQL interview question (19) -- Tiktok -- select the list of users who have logged in for two consecutive days every month

Multimedia architecture -- Introduction to display

Backup the method of uploading babies in Taobao stores to multiple stores

Matlab uses deep learning recurrent neural network RNN long-term and short-term memory LSTM to predict waveform time series data

Coursera self driving car Part4 motion planning finalproject principle and key code analysis
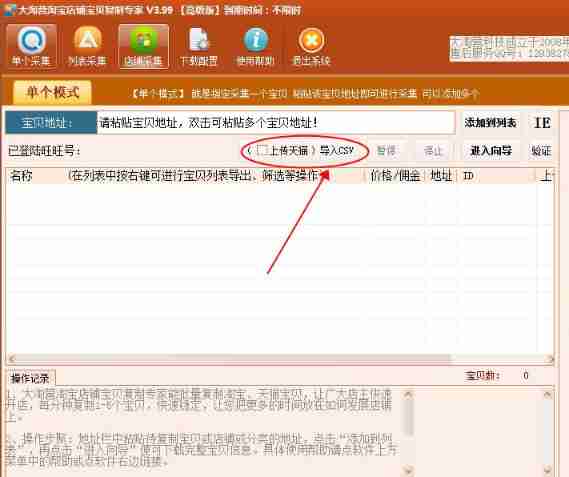
How to import and upload a CSV generated by a third-party platform to a Taobao store
随机推荐
7、 Picker component
Open version - user level
Wechat games (5)
Multi camera data collection based on Kinect azure (III)
Error e: unable to locate package sudo
Shutter margin negative margin
How to solve 'webdriver' object has no attribute 'switch_ to_ window‘
EditText and Scrollview focus grabbing
antd 框架:点击链接重开浏览器页面——基础积累
Canoe learning notes (3) graphic window introduction diagram
Lean production | lean management
White paper on Web page quality of Baidu search engine guides website construction and optimization
Mid year summary of 33 year old programmer
Selenium anti crawl and analog mobile browser
Open version - inventory description
4、 Button component
How to import Taobao products into another store
6、 Scrollview component
简单是最好的网络推广的方法
由浅入深拿下OpenFeign