The essence of linear algebra 6 inverse matrix, column space and zero space

Catalog

One 、 System of linear equations ​​​​​​​

Two 、 Inverse matrix

1. Concept  

2. Solve the equation  

  3、 ... and 、 Rank （rank）

Four 、 Column space

5、 ... and 、 Zero space / nucleus

---

 

One 、 System of linear equations

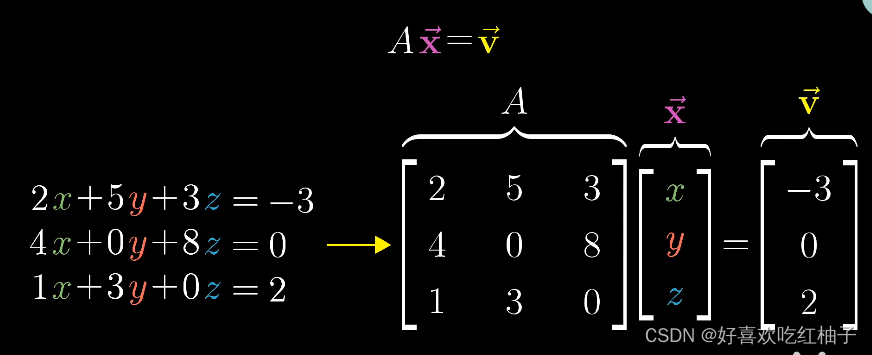
No power , A system of equations in which each equation is primary with respect to the unknown quantity ( for example 2 element 1 Subequation system ）

The solution of linear equations can correspond to the multiplication rule of matrices , Write the matrix as shown in the figure below A* vector x= vector v In the form of

Geometric meaning ： Find a vector v, So that it is related to a vector that has undergone a linear transformation x coincidence

Two 、 Inverse matrix

1. Concept  

When A The determinant of is not 0 when ：A matrix *A The inverse matrix of a vector can return the vector to its original state , Go back to i and j yes [1,0] and [0,1] The state of

be called Identity transformation

 

2. Solve the equation  

  Once found A The inverse matrix , You can multiply left and right A To solve the equation

Geometric meaning ： Through vectors v The inverse transformation of is reduced to x

  3、 ... and 、 Rank （rank）

Four 、 Column space

  There are many kinds of transformation results of a three-dimensional matrix , If it is not compressed , The output result is three-dimensional space （ Rank =3）, If it is compressed , The output result can be a plane （ Rank =2） Or straight line （ Rank =1）, The set of all these possible transformations is called the matrix Column space , The zero vector must be contained in the column space

Column space is the space that the columns of a matrix form

The role of column spaces ： When not used A When solving the equations with the inverse matrix of , The existence of column spaces lets us know when solutions exist  

5、 ... and 、 Zero space / nucleus

The set of vectors that fall at the origin after transformation