[reading notes > statistics] 12-01 construction of confidence interval - Introduction to the concept of confidence interval

Confidence interval construction

introduction

The previous chapter helps us use samples to estimate the population mean 、 The exact value of variance or a certain proportion . But the sample you think must be accurate （ Or unbiased ） Do you ？ This chapter , Another way to estimate population statistics —— confidence interval , It has its function .

---

Mandy candy company uses a containing 100 The point estimator of the mean taste duration obtained from the sample of sugar balls is 62.7 minute , At the same time, the point estimator of the total variance is 25 minute . This is the most reliable estimate of taste duration possible based on the evidence at hand , But if there is a slight difference , So what do we do? ？

We did use the most representative data sample , In order to estimate the main statistics of the population , Mean value 、 variance 、 The proportion , This means that the point estimator of the mean taste duration of the super long effect gum ball is the best estimate we can give .

But there is such 2 A question ：

1. We rely on results from a single sample to arrive at very accurate estimates . We try our best to make it unbiased , Make it representative . But can it 100% Represents the overall , We are not absolutely sure , The reason is simple —— We use samples .
2. If the sample we use is unbiased , Then this estimator is likely to be close to the truth of the whole . The problem is , How close is it “ Close enough ”？

---

therefore , Instead of giving an exact value as an estimate of the overall mean , It's better to adopt another method . We can specify a certain interval —— Instead of using a very precise length of time , As an estimate of the duration of sugar ball taste . for example , We can say ： We expect the taste duration of sugar balls to be 55 to 65 minute , This will still make listeners feel that the duration of sugar ball taste is close 1 Hours , But there is a bigger one Error space . Determining the width of the space depends on how confident you are about the result .

confidence interval

Know the confidence interval

before , We are based on sample data , Using point estimator, the mean duration of sugar ball taste was estimated , Through point estimator , We can give a very accurate estimate of the average duration of sugar ball taste . The following figure shows the distribution of taste duration of sugar ball samples .

that , If we specify an interval for the overall mean , What will happen ？ We don't specify an exact value , And specify two values — We expect the duration of sugar ball taste to be between these two values . Let's put the point estimator of the mean at the center of this interval , And set the upper and lower limits of this interval as the point estimator plus or minus some error .

The upper and lower limits of the interval are selected to make “ The overall average is between a and b Between ” This result has a specific probability . for example , You may want to choose a and b, The probability of including the overall mean in this interval is 95%. in other words , The chosen a and b bring ：
$$P(a<\mu <b)=0.95$$
We use it (a,b) I mean this interval , because a and b The exact value of depends on what you want to do with “ This interval contains the overall mean ” The credibility of this result , therefore ,(a,b) go by the name of confidence interval .

that , How do we find the confidence interval of the overall mean ？

There are four steps to solve the confidence interval

1. choice Overall statistics （ It refers to the total statistics that you want to use to build confidence intervals ）
2. Find its sampling distribution （ The previous chapter talked about sampling distribution ）
3. Determine the confidence level （ The interval you choose contains the probability of this statistic ）
4. Find the upper and lower confidence limits （ In order to find the upper and lower confidence limits , We need to know the confidence level and sampling distribution ）

The first 1 Step ： Select the population statistics

The first 1 The first step is to select the statistics for which the confidence interval is to be constructed , It depends on the actual problem to be solved .

In our case , It is necessary to build a confidence interval for the mean duration of gum ball taste , So it needs to be the overall average $\mu$ Build a confidence interval .

The first 2 Step ： Find the sampling distribution of the selected statistic

In order to find the sampling distribution of the population mean , We need to know the sampling distribution of the mean , I need to know $\overline{X}$ And its distribution .（ amount to “ The probability of sample mean in the previous chapter ” In turn, , What we know this time is the probability of the sample mean , What is required is the overall mean and variance ）

Let's first find the expectation and variance . Review the previous chapter , We know the sampling distribution of the mean （ Concept ： Use the mean of all samples from all possible samples to form a distribution ） The expectation and variance of is ：
$$\begin{gathered} E(\overline{X})=\mu \\ Var(\overline{X})=\frac{{\sigma }^2}{n} \end{gathered}$$
In order to use the above results to find $\mu$ The confidence interval of , We substitute the value of the population variance ${\sigma }^2$ And sample size n. But we don't substitute $\mu$ The numerical , Because this is because we are calculating the confidence interval for this value .（$\mu$ Is the overall mean , We are finding the confidence interval for it ）

reason （ Maybe you can understand it later ）： We are using sampling distribution to find $\mu$ The confidence interval of , therefore , except $\mu$ outside , We substitute all the values . Plug in ${\sigma }^2$ and n after , Can use $\overline{X}$ Find the confidence interval , We will explain it soon .

But there's a problem —— We don't know ${\sigma }^2$ Of Truth value , Estimates must be made based on samples . What do I do ？

-> utilize Point estimator

Although we don't know the total variance ${\sigma }^2$ True value of , But it can be estimated with its point estimator . So we substitute ${\hat{\sigma }}^2$（ Point estimator of population variance , See the previous chapter for the concept ）, Or called $s^2$, instead of ${\sigma }^2$.（ It means to use ${\hat{\sigma }}^2$ Roughly make do with it when ${\sigma }^2$）

So the mean and variance of the sampling distribution of the mean are equal to ：
$$\begin{gathered} E(\overline{X})=\mu \\ Var(\overline{X})=\frac{s^2}{n} \end{gathered}$$
（ Again ：$s^2$ Is the point estimator of variance . We don't know the true value of the total variance , So we use the sample variance to estimate .）

Mandy confectionery company uses contains 100 Calculate the estimated value of a sample of sugar balls , And calculate $s^2=25$, therefore ：
$$Var(\overline{X})=\frac{s^2}{n}=25/100=0.25$$
besides , We also need to know clearly $\overline{X}$ The distribution of .

The first 3 Step ： Determine the confidence level

The confidence level indicates You want to be interested in “ Confidence intervals contain population statistics ” How sure is this statement . for example , Suppose we want the confidence level of the overall mean to be 95%, This means that the probability that the overall mean is in the confidence interval is 0.95.

Be careful ： The higher the confidence level , The wider the range , The greater the probability that the confidence interval contains population statistics .

Choose a reasonable confidence level , It can guarantee a high probability , And make the interval narrow enough . Otherwise, for example ： We can say that the average duration of sugar ball taste is 0 to 3 Between days , But you can't know how long the taste of sugar balls actually lasts .

The first 4 Step ： Find the upper and lower confidence limits

The last step is to ask a and b— Confidence interval Upper and lower limit , The upper and lower bounds indicate the left and right boundaries of a range — The average is 95% The probability of falling into this range .a and b The exact value of depends on the sampling distribution to be used and the confidence level to be possessed .

For our example , We need to make the mean duration of sugar ball taste have 95% The degree of confidence , namely ,$\mu$ Located in the a and b The probability between must be 0.95. We also know that ,$\overline{X}$ In line with the normal distribution , among $\overline{X}～N(\mu ,0.25)$.

utilize $\overline{X}$ We can find the distribution of a and b Value . namely , We can use $\overline{X}\sim N(\mu ,0.25)$ Find out a and b, for example $P(\overline{X}<a)=0.025$ and $P(\overline{X}>b)=0.025$.

because $\overline{X}$ In line with the normal distribution , So we can Find the confidence interval with normal distribution . The method is similar to the algorithm mentioned above ： Calculate the standard score , Query the standard normal distribution probability table , Get the desired results .

1 seek Z

Yes $\overline{X}$ Standardize .
$$Z=\frac{\overline{X}-\mu }{\sqrt{0.25}},amongZ\sim N(0,1)$$
The following is the normalized confidence interval graph ：

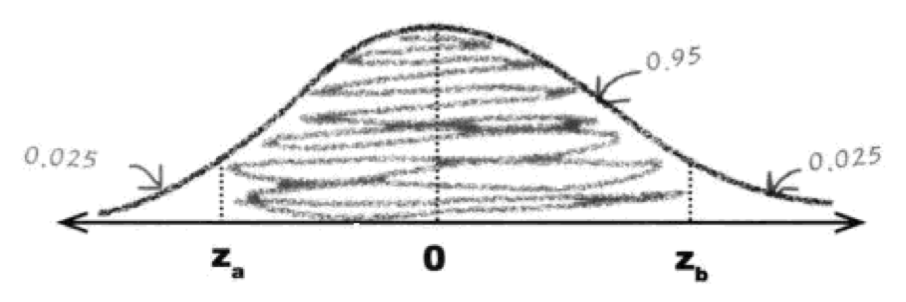
utilize $P(Z<z_a)=0.025$ and $P(Z>z_b)=0.0255$ We can work out $z_a,z_b$, They are the upper and lower limits of the standard confidence interval .

2 use $\mu$ Rewrite inequality

Only this and nothing more , We get $P(-1.96<Z<1.96)=0.95$, namely ：
$$P(-1.96<\frac{\overline{X}-\mu }{0.5}<1.96)=0.95$$
use $\mu$ Rewrite inequality , You can get $\mu$ The confidence interval of .
$$\begin{gathered} -1.96<\frac{\overline{X}-\mu }{0.5}<1.96 \\ -0.98<\overline{X}-\mu <0.98 \\ \overline{X}-0.98<\mu <\overline{X}+0.98 \end{gathered}$$
3 Finally, ask for $\overline{X}$ The numerical

Write the inequality , We are very close to the value describing the typical taste duration of sugar balls ——$\mu$ The confidence interval of . namely , We use ：
$$P(\overline{X}-0.98<\mu <\overline{X}+0.98)=0.95$$
Here is the sketch ：

Then just ask for the money $\overline{X}$, We can get the upper and lower confidence limits .

$\overline{X}$ refer to The distribution of the sample mean , So we can use samples from Mandy candy company $\overline{x}$ value （ The term is ： Sample mean ）.

Tips ： There is no substitute , See the following for specific reasons “ ask 2”.$Var(\overline{X})=\frac{{\sigma }^2}{n}$ Medium ${\sigma }^2$ Because it is the total variance , Using the total variance point estimator $s^2$ replace .

In this way, the confidence interval is obtained . In the interval (61.72,63.68) The probability of including the overall mean duration of sugar ball taste in 95%.

Use confidence intervals instead of point estimators , An accurate and accurate estimation of the taste duration of sugar balls is given , There is no need to mention precise figures —— Even if the sample has errors, there is still room for maneuver .

Step summary

Let's review the previous steps of confidence interval construction .

First Select the population statistics used to construct the confidence interval . We need to find the confidence interval of the mean duration of sugar ball taste , So we need to build the confidence interval of the mountain .

After determining the total statistics used to construct the confidence interval , next Find its sampling distribution . We obtain the expectation and variance of the sampling distribution of the mean , Substitute in Division M The value of each statistic other than , So we found that we can use the normal distribution of the text .

And then , We determined the confidence level used to construct the confidence interval ——95%.

In the end, it must Find the upper and lower confidence limits of the confidence interval . We use the confidence level and sampling distribution to get the appropriate confidence interval .

---

The same steps are used repeatedly to build confidence intervals , Therefore, some simplification can be made , It depends on the required confidence level and the distribution of test statistics . As follows , Just look at the overall estimate required 、 Overall distribution and various conditions , Then substitute the population statistics or its estimators , That's it . The number c Depends on the confidence level .

The example above should be No 3 In this case .

Example （ Just substitute ）

ask ： Ask before $\overline{X}$ Of expectations and variances , Why substitute ${\sigma }^2$ Point estimator of , But do not substitute $\mu$ Point estimator of ？

answer ： Because what we need is $\mu$ The confidence interval of , So there's no need to $\overline{x}$ Instead of $\mu$. We need to find the content $\mu$ The expression of , In order to find the confidence interval .

ask ： Why $\overline{x}$ As $\overline{X}$ Value ？

answer ：$\overline{X}$ The distribution of is the sampling distribution of the mean . This is how it came ： Take each size from the total as n Possible samples of , Then use the mean value of all samples to form a sampling distribution .

$\overline{x}$ Is the specific mean value from the sample , So we use it to find the confidence interval .

ask ： What is the difference between confidence interval and confidence level ？

answer ： The confidence level is “ The statistics are in the confidence interval ” Probability , Usually a percentage , for example 95%. The confidence interval gives the interval itself —— The upper and lower limits of the actual range of numbers .

ask ： We have obtained $\mu$ Of 95% The confidence interval is (61.72, 63.68), What exactly does this mean ？

answer ： It means ： If you plan to take multiple samples of the same size , Then build confidence intervals for all these samples , Then there are 95% Will contain the true value of the overall mean . From this you know , The confidence interval constructed by this method is 95% In all cases, it will include the overall mean .

ask ： Are all confidence intervals based on normal distribution ？

answer ： Is not the case, . We will then talk about intervals based on other distributions .

ask ： Since it's just a matter of substituting numerical values into a simple algorithm , Why are there so many steps ？

answer ： These steps are to let you see the essence of the problem , Understand the construction process of confidence interval . Most of the time , You just need to insert the value .

ask ： Is it necessary to make continuity correction when using confidence intervals ？

answer ： Theoretically, yes , However, it is often ignored in practice , That is to say, it is only necessary to calculate the confidence interval by substituting the numerical value in the simple algorithm .