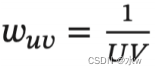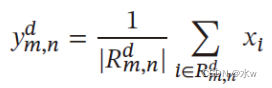当前位置:网站首页>深度学习之 10 卷积神经网络1
深度学习之 10 卷积神经网络1
2022-08-03 09:01:00 【水w】
上一篇我们了解了前馈神经网络的基础概念知识之后,本文是接着上一篇深度学习之 9 前馈神经网络2:实现前馈神经网络,模型调优_水w的博客-CSDN博客
目录
前言
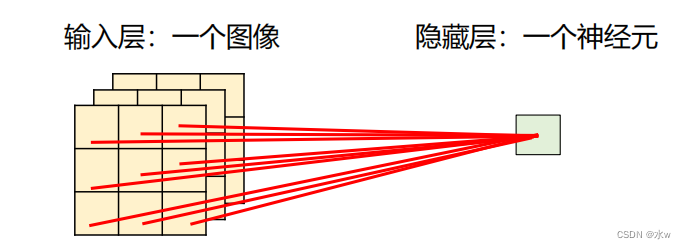
在用全连接前馈网络来处理图像时, 存在以下两个问题:① 参数太多假设输入一个100×100×3的图像;隐藏层只有一个神经元,则它与输入层之间有30,000个互相独立的连接,每个连接都对应一个权重参数;随着隐藏层神经元数量的增多,参数的规模也会急剧增加。这会导致整个神经网络的训练效率非常低,也很容易出现过拟合。
② 局部不变性特征难以提取自然图像中的物体都具有局部不变性特征,缩放、平移、旋转等操作不影响其语义信息;全连接前馈网络很难提取这些局部不变性特征,一般需要进行数据增强来提高性能;
感受野(Receptive Field)机制主要是指听觉、视觉等神经系统中一些神经元的特性,即神经元只接受其所支配的刺激区域内的信号。卷积神经网络(Convolutional Neural Network, CNN)是受生物学上感受野机制的启发而提出的;卷积神经网络有三个结构上的特性:局部连接、权重共享以及池化;卷积神经网络一般是由卷积层、池化层和全连接层交叉堆叠而成的前馈神经网络;卷积神经网络具有一定程度上的平移、缩放和旋转不变性;与全连接神经网络相比,卷积神经网络的参数更少;
1 卷积运算
(1)一维卷积
卷积(Convolution)是分析数学中一种重要的运算。在信号处理或图像处理中,经常使用一维或二维(离散)卷积。一维卷积经常用在信号处理中,用于计算信号的延迟累积。

* 设滤波器长度为𝐾,它和一个信号序列𝑥1, 𝑥2, ⋯的卷积为:
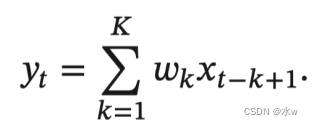
* 以向量的形式表示为:
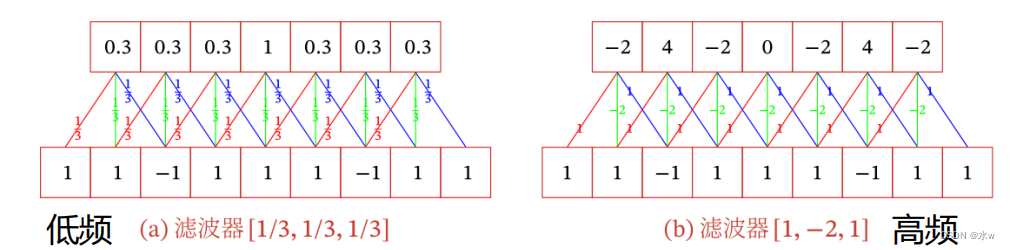
增加卷积的多样性,可以更灵活地进行特征处理;
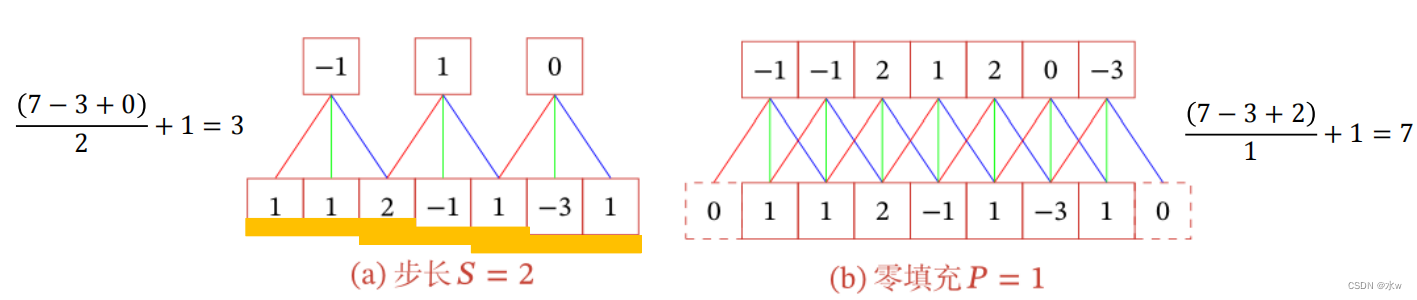
在卷积的标准定义基础上,引入滤波器的滑动步长𝑆和 零填充𝑃;* 步长𝑆 (Stride)是指卷积核在滑动时的时间间隔。* 零填充𝑃 (Zero Padding)是在输入向量两端进行补零。
假设卷积层的输入神经元个数为𝑀,卷积大小为𝐾 ,步长为𝑆,在输入两端各填补𝑃个 0(zero padding),那么该卷积层的神输出经元数量为 (𝑀 − 𝐾 + 2𝑃)/𝑆 + 1卷积的结果按输出长度不同可以分为三类(𝐾表示卷积核长度):* 窄卷积:步长 𝑆=1,两端不补零 𝑃=0 ,卷积后输出长度为 𝑀 − 𝐾 + 1;* 宽卷积:步长 𝑆=1,两端补零 𝑃=𝐾 − 1 ,卷积后输出长度 𝑀 + 𝐾 − 1;* 等宽卷积:步长 𝑆=1,两端补零 𝑃=(𝐾 − 1)/2 ,卷积后输出长度 𝑀;• 在早期的文献中,卷积一般默认为窄卷积。• 而目前的文献中,卷积一般默认为等宽卷积。
(2) 二维卷积
二维卷积经常用在图像处理中。因为图像为一个二维结构,所以需要将一维卷积进行扩展。
* 给定一个图像𝑿 ∈ 𝑹𝑴×𝑵 和一个滤波器𝑾 ∈ 𝑹𝑼×𝑽 ,一般𝑈<<𝑀, 𝑉<<𝑁,其卷积为:
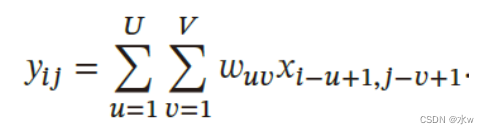
* 输入信息 𝑿 和滤波器 𝑾 的二维卷积定义为: 二维卷积 𝒀 = 𝑾 ∗ 𝑿
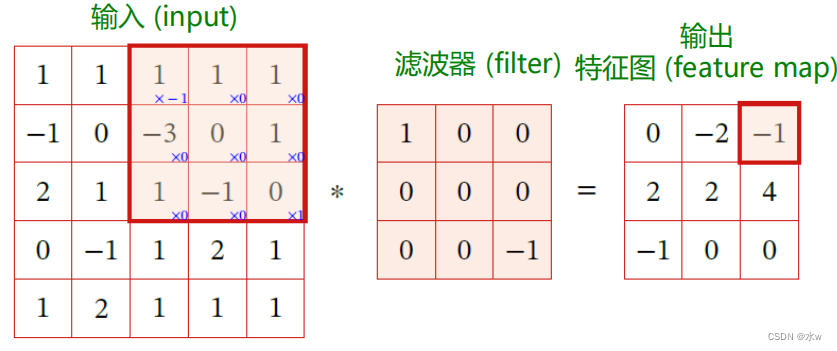
(3)特征映射
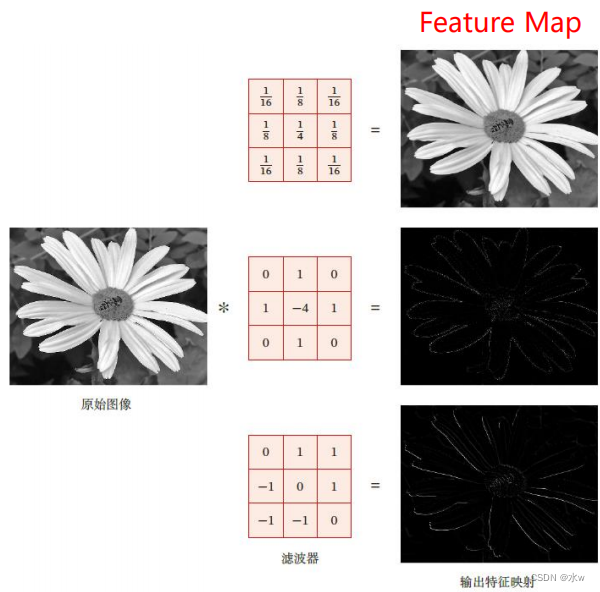
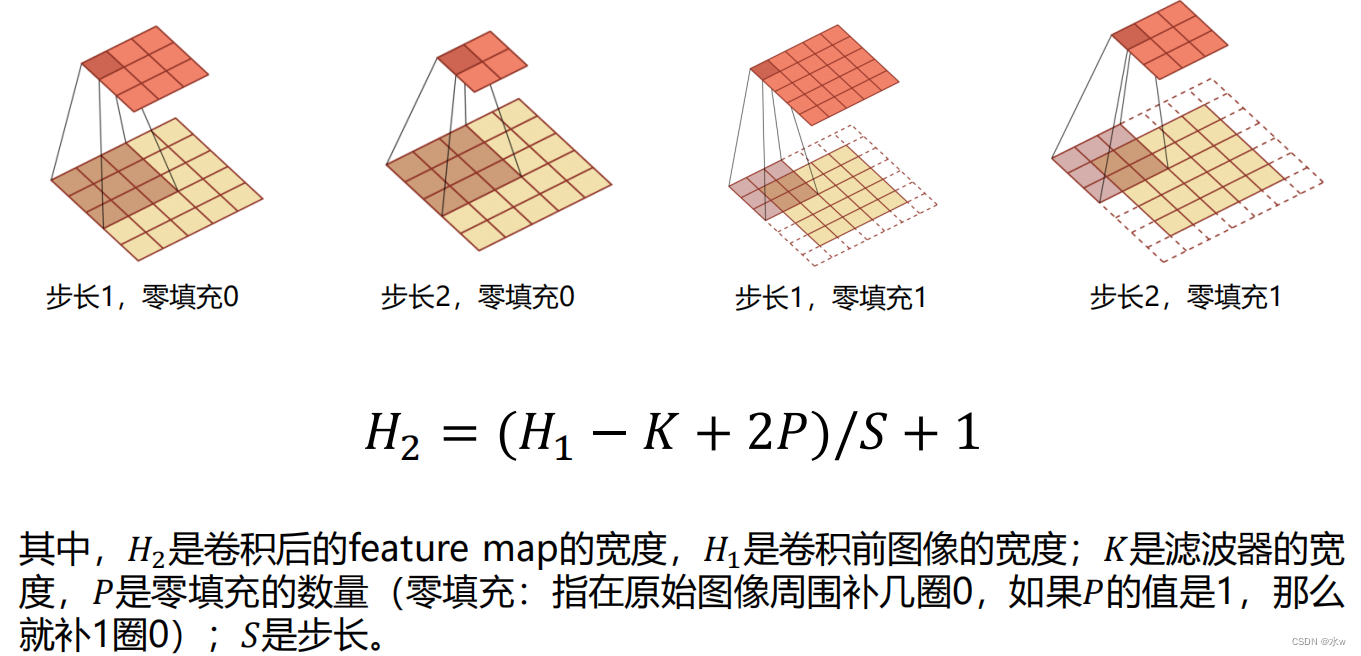
一幅图像在经过卷积操作后得到结果称为特征映射 ( Feature Map )。输入图像经过一个卷积核处理后的输出为一个Feature Map.在图像处理中常用的均值滤波(Mean Filter), 将当前位置的像素值设为滤波器窗口中所有像素的平均值,即右图给出在图像处理中几种常用的滤波器,以及其对应的特征映射。最上面是高斯滤波器,对图像进行平滑去噪;中间和最下面的滤波器用来提取边缘特征。
(3)互相关运算
根据卷积运算的原始定义,计算卷积的过程中,需要进行卷积核翻转。在具体实现上,一般会以互相关操作来代替卷积,从而会减少不必要的翻转操作。互相关(Cross-Correlation)是一个衡量两个序列相关性的函数,通常是用滑动窗口的点积计算来实现。在神经网络中使用卷积是为了进行特征抽取,卷积核是否进行翻转和其特征抽取的能力无关。特别是当卷积核是可学习的参数时,卷积和互相关在能力上是等价的。为了实现上的方便起见,很多深度学习工具中卷积操作其实都是互相关操作。互相关和卷积的区别仅仅在于卷积核是否进行翻转。因此互相关也可以称为不翻转卷积。
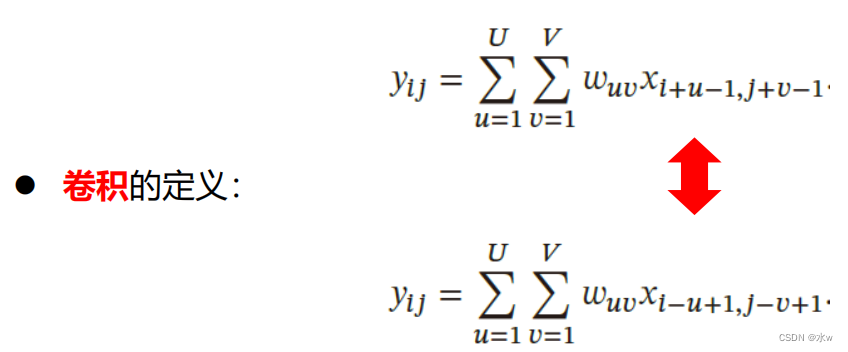
给定一个输入信息𝑿 ∈ ℝ𝑀×𝑁和滤波器𝑴 ∈ ℝ𝑈×𝑉 的二维互相关定义为: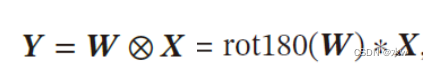
其中⊗表示互相关运算,rot180(⋅) 表示旋转180 度,𝒀 ∈ ℝ𝑀−𝑈+1,𝑁−𝑉 +1为输出矩阵
2 卷积网络的动机:参数共享,稀疏交互,平移不变性
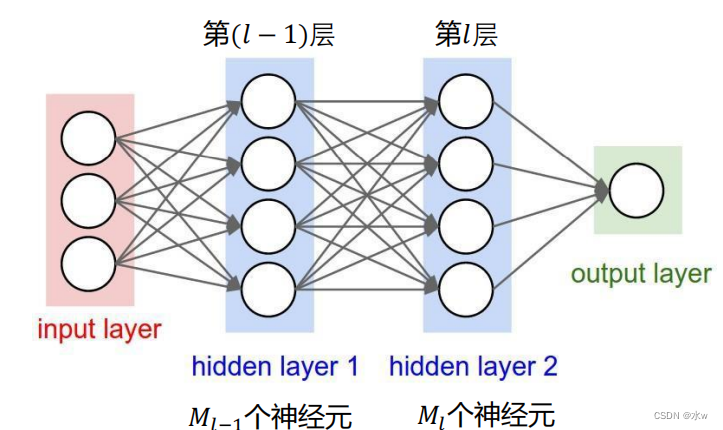
在全连接前馈神经网络中,如果第𝑙层有𝑀𝑙个神经元,第𝑙 − 1层有𝑀𝑙−1个神经元,则连接边有𝑀𝑙 × 𝑀𝑙−1个,也就是权重矩阵有𝑀𝑙 × 𝑀𝑙−1参数。当𝑀𝑙 和𝑀𝑙−1 都很大时,权重矩阵的参数非常多,训练的效率会非常低。
那么,
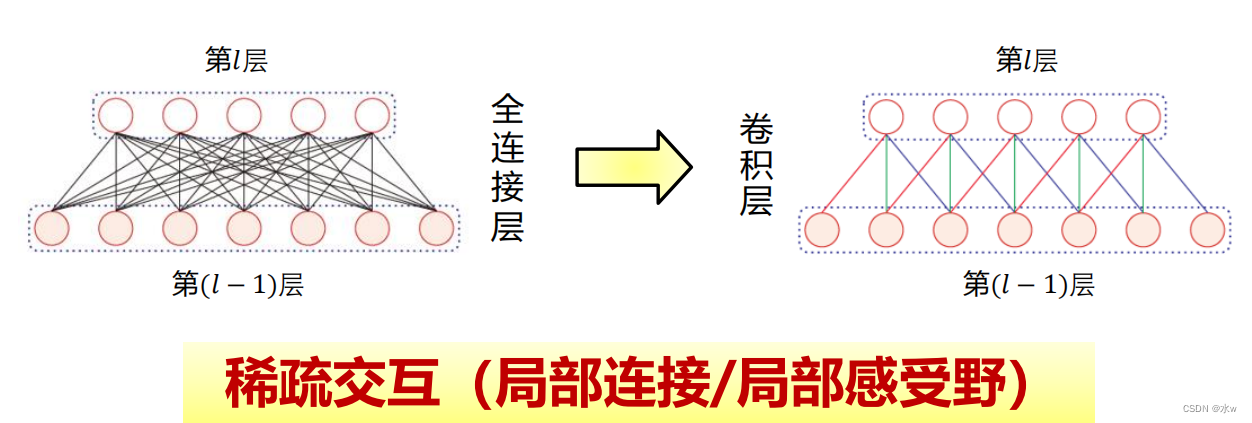
把连接稀疏化:参数变少,模型变简单,降低过拟合可能性
在卷积层(假设是第𝑙层)中的每一个神经元都只和下一层(第𝑙 − 1层)中某个局部窗口内的神经元相连,构成一个局部连接网络。这样,卷积层和下一层之间的连接数大大减少,由原来的𝑀𝑙 × 𝑀𝑙−1个连接变为𝑀𝑙 × 𝐾个连接,𝐾 为卷积核大小
参数共享
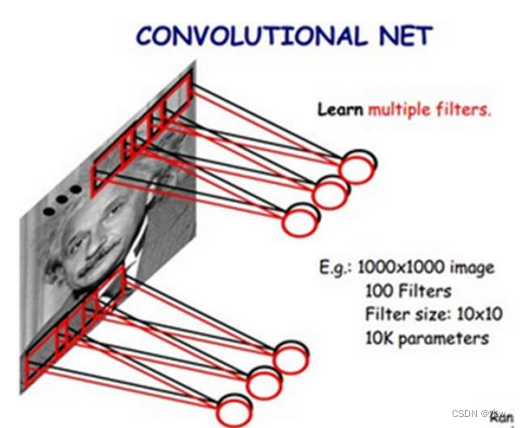
*给定1000x1000像素的图像,假设神经网络具有1百万个隐藏层神经元,则全连接需要1012个权值参数;
*局部感受野是10x10,隐藏层每个感受野只需要和这10x10的局部图像相连接, 所以1百万个隐藏层神经元就只有一亿个连接,即108个参数。

平移不变性:由卷积+池化共同实现
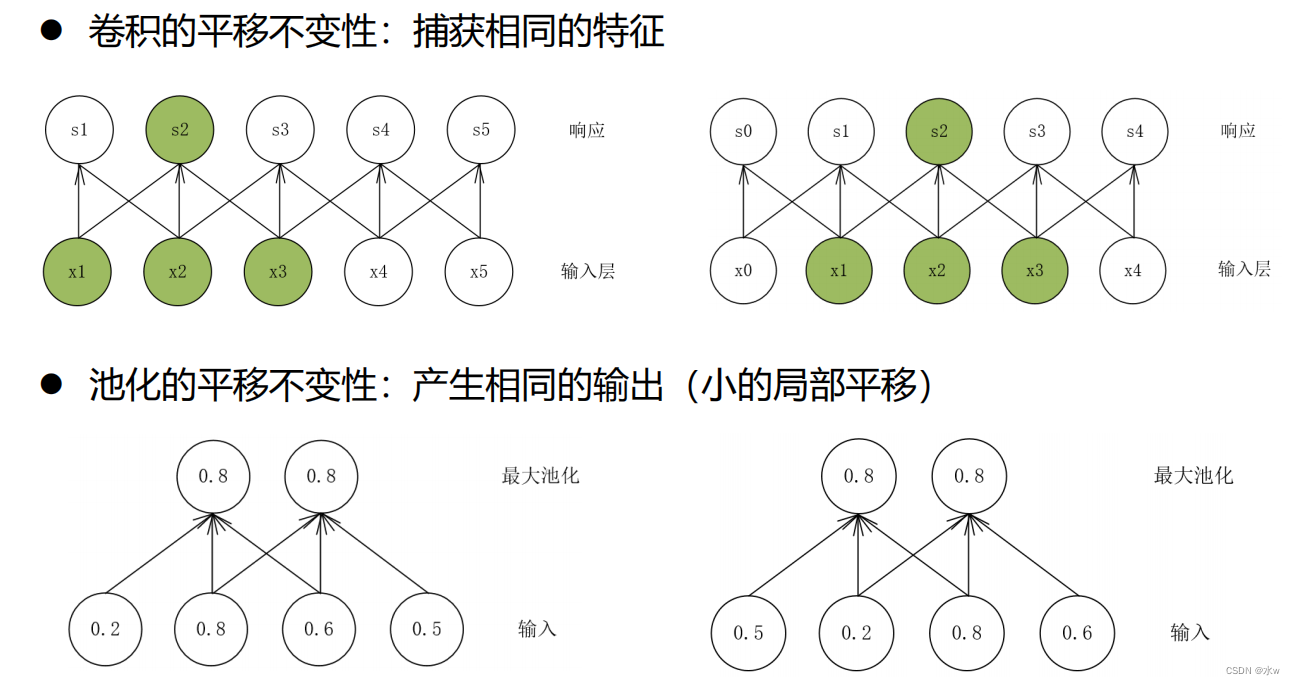
卷积网络具有平移不变性,它是由卷积+池化共同实现的。卷积:图像经过平移后,通过卷积运算仍然能够捕捉到同样的特征。池化:图像经过平移后,通过池化操作仍然能够产生相同的输出。平移是一种几何变换 ,表示把一幅图像或一个空间中的每个点在相同方向移动相同距离。
例如:对图像分类任务来说,图像中的目标不管被移动到哪个位置,分类结果(标签)应该是相同的。平移不变性意味着系统产生完全相同的响应(输出),不管它的输入是如何平移的。
*输入图像的左下角有一个人脸,经过卷积,人脸的特征(眼睛,鼻子)也位于特征图的左下角。
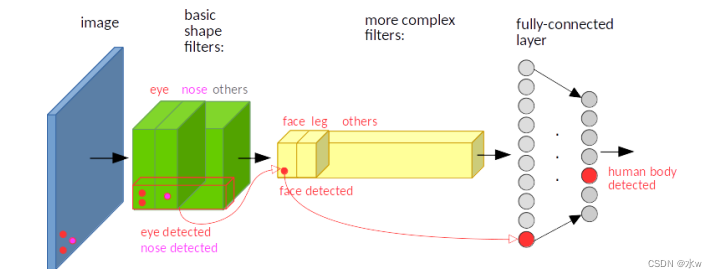
*假如人脸特征在图像的左上角,那么卷积后对应的特征也在特征图的左上角。
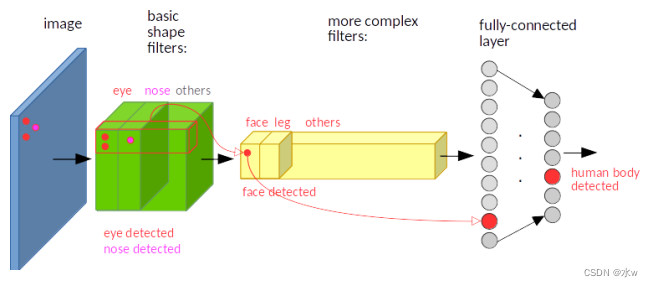
3 池化,最大池化,平均池化
池化层(Pooling Layer)也叫子采样层(Subsampling Layer),其作用是进行特征选择, 降低特征数量,从而减少参数数量。卷积层虽然可以显著减少网络中连接的数量,但特征映射组中的神经元个数并没有显著减少。如果后面接一个分类器,分类器的输入维数依然很高,很容易出现过拟合。为了解决这个问题,可以在卷积层之后加上一个池化层,从而降低特征维数,避免过拟合。卷积层的输入神经元个数为𝑀,卷积大小为𝐾 ,步长为𝑆,在输入两端各填补𝑃个 0 (zero padding),那么该卷积层的神输出经元数量为 (𝑀 − 𝐾 + 2𝑃)/𝑆 + 1
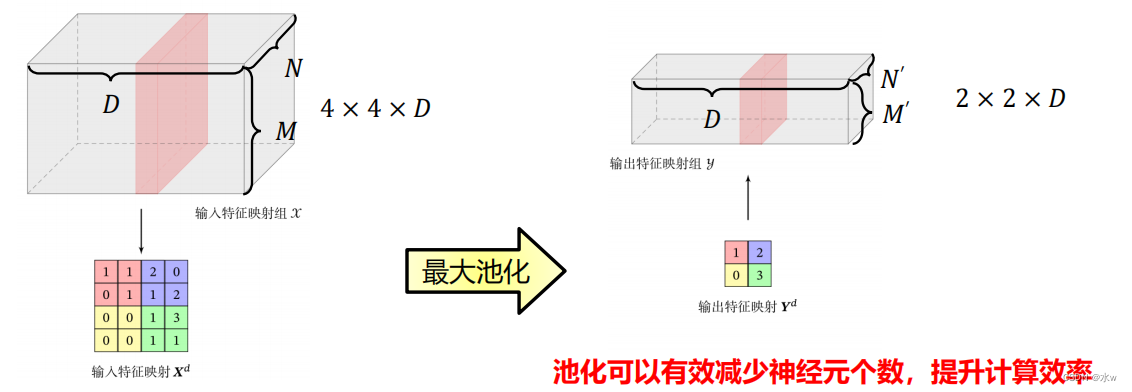
池化(Pooling)是指对每个区域进行下采样(Down Sampling)(原来有很多个样本,在多个样本中选一个或几个)得到一个值,作为这个区域的概括。*可以有效减少神经元的个数,提升计算效率;
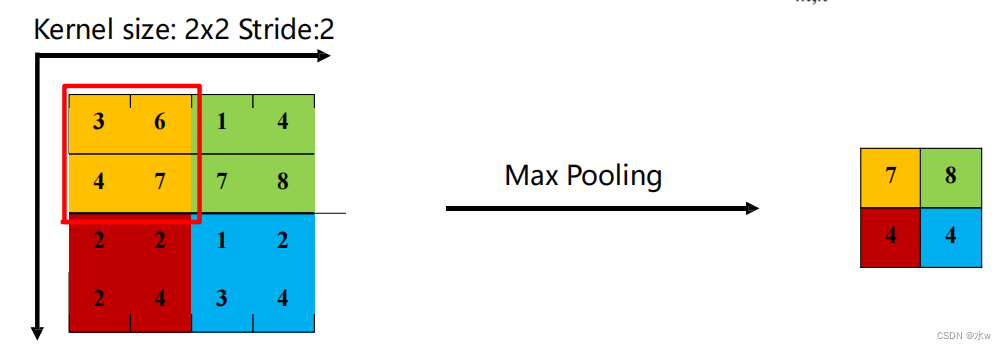
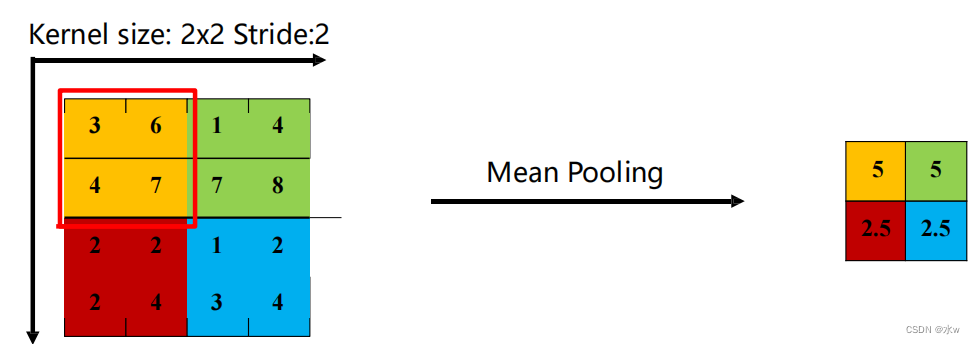
最大池化(Maximum Pooling 或Max Pooling):对于一个区域𝑅𝑚,𝑛 𝑑 ,选择这个区域内所有神经元的最大活性值作为这个区域的表示。*不但可以有效地减少神经元的数量,还可以使得网络对一些小的局部形态改变保持不变性,并拥有更大的感受野。平均池化(Mean Pooling):一般是取区域内所有神经元活性值的平均值*主要用来抑制邻域值之间差别过大造成的方差过大。
边栏推荐
猜你喜欢
随机推荐
BOM系列之localStorage
好用的插件
RSTP(端口角色+端口状态+工作机制)|||| 交换机接口分析
pytorch one-hot tips
计算机网络之网络安全
Guava的Service
二进制日志过期时间设置expire_logs_days
批量将PNG格式转化为JPG格式
【TPC-DS】25张表的详细介绍,SQL的查询特征
gpnmb+ gpnmb-AT2 cell idling mapping Epithelial cell idling mapping
Unity关于编辑器扩展自定义标签,方便扩展Inspector
dflow入门2——Slices
HCIP实验(06)
【微信小程序】底部有安全距离,适配iphone X等机型的解决方案
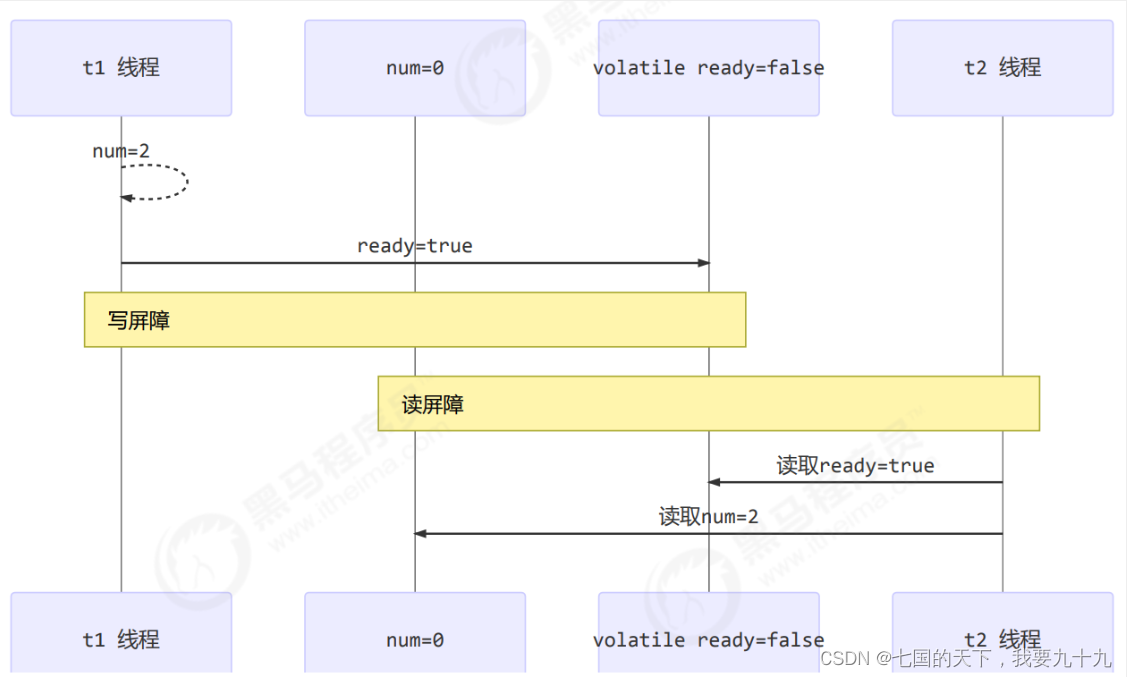
内存模型之有序性
牛客 - 鼠标的天选(字符串哈希)
关于Unity自定义Inspector面板的一些自定义编辑器扩展
Redis集群概念与搭建
AcWing 3391. 今年的第几天?(简单题)
获取JDcookie的方法