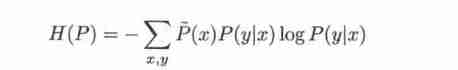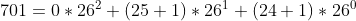C language black Technology: Archimedes spiral! Novel, interesting, advanced~

Program Introduction

At first, I wanted to use Archimedes spiral to realize visualization π, So I learned Taylor expansion calculation π The process of , Similarly, drawing inferences from one instance realizes the calculation e  The process of , Learned to draw Archimedes spiral . Later, another kind of “ The straight line of walking ”, To visualize rational numbers . This program combines all functions , Realize using spiral line and walking line , To visualize irrational numbers π, Irrational number e  And rational numbers .

Calculation π, Calculation e  The process of , Taylor expansion is used . I don't know if it's a coincidence ,π The first two items of and , And e  The first four sums of are 2.666 .... And coincidentally, each term of these two irrational Taylor expansions is actually “ contain ” Last item .π No i  Term is the multiplication of the previous term i/( 2 i+1),e No i  Term is the multiplication of the previous term 1/i, Such a structure makes the calculation much simpler ; It also seems to give me a way to create new irrational numbers , For example, each term is the multiplication of the previous term 1/( 2 i), Although this may not have practical significance , I can't prove it to be irrational , But it's interesting ^-^.

You should have a deep understanding of the first multiplication in the references , From low to high ; After division , From high to low , Multiply the remainder by ten and add it to the next digit , Stay in business ; Finally add , From low to high , Super decimal . I'll take the rest , The retention business is reversed , Made me for a while .

π More than 700 people will appear 6  A continuous 9, The pictures are also displayed .

The process of constructing Archimedes spiral , There are changes , Because I don't want simple lines , I want to string circles on the line , So I draw a circle on the track , The number of circles is also limited （ This procedure is initially 1000, This can be programmed ）. So if you just want to test the properties of Archimedes spiral alone , It is necessary to separate the function of drawing helix , Change the process of drawing a circle to drawing a line , Or put the radius of the small circle （d） Change a little , Approximate dash ; Then change the cycle condition .

Walking numbers , According to the reference materials . The rules in the video are ambiguous , I push back according to the video , According to the law, the image in his video can be restored . But according to the law , The argument that rational numbers he wrote in the video can form centrosymmetric graphs should be wrong .

There is a small discovery in writing , I didn't go into it , When the denominator is some prime number , The length of the cyclic section is these prime numbers minus one , That is, the maximum cycle section length that can be obtained by this number is reached . First of all, this law should have nothing to do with molecules , Then there is the law that not all prime numbers hold , This distinguishes at least two classes of prime numbers , Or at least two kinds of numbers .

Palette is also an independent program , This is a tool that used to be convenient for me to find colors . Now the teacher has given a perfect replacement tool , Let him play in this program . This palette also uses my favorite way of constructing two-dimensional coordinates of a hexagon with three-dimensional parameters , There will be programs using this method in the future .

 

Program execution effect

 

If the source code is a little long, I won't put it on , Interested partners can enter the group and download by themselves ~

- End -

————————————————

Whether you change careers or not , It's better to be a beginner , It's OK to be advanced , If you want to learn programming ~

【 Worthy of attention 】 my   Programming learning exchange Club 【 Click to enter 】

————————————————